Controlador de circuito cerrado

Un controlador de lazo cerrado o controlador con retroalimentación es un lazo de control que incorpora retroalimentación , en contraste con un controlador de lazo abierto o controlador sin retroalimentación . Un controlador de lazo cerrado utiliza retroalimentación para controlar estados o salidas de un sistema dinámico . Su nombre proviene de la ruta de información en el sistema: las entradas del proceso (por ejemplo, voltaje aplicado a un motor eléctrico ) tienen un efecto en las salidas del proceso (por ejemplo, velocidad o torque del motor), que se mide con sensores y es procesado por el controlador; el resultado (la señal de control) se "realimenta" como entrada al proceso, cerrando el lazo. [1]
En el caso de los sistemas de retroalimentación lineal , se organiza un bucle de control que incluye sensores , algoritmos de control y actuadores en un intento de regular una variable en un punto de ajuste (SP). Un ejemplo cotidiano es el control de crucero en un vehículo de carretera; donde las influencias externas como las colinas causarían cambios de velocidad, y el conductor tiene la capacidad de alterar la velocidad establecida deseada. El algoritmo PID en el controlador restaura la velocidad real a la velocidad deseada de una manera óptima, con un retraso o sobreimpulso mínimo , controlando la salida de potencia del motor del vehículo. Los sistemas de control que incluyen algún tipo de detección de los resultados que intentan lograr hacen uso de la retroalimentación y pueden adaptarse a circunstancias variables hasta cierto punto. Los sistemas de control de bucle abierto no hacen uso de la retroalimentación y funcionan solo de formas preestablecidas.
Los controladores de circuito cerrado tienen las siguientes ventajas sobre los controladores de circuito abierto:
- Rechazo de perturbaciones (como colinas en el ejemplo de control de crucero anterior)
- Rendimiento garantizado incluso con incertidumbres del modelo , cuando la estructura del modelo no coincide perfectamente con el proceso real y los parámetros del modelo no son exactos
- Los procesos inestables pueden estabilizarse
- Sensibilidad reducida a las variaciones de parámetros.
- Rendimiento mejorado del seguimiento de referencias
- Rectificación mejorada de fluctuaciones aleatorias [2]
En algunos sistemas, se utilizan simultáneamente el control de bucle cerrado y el de bucle abierto. En dichos sistemas, el control de bucle abierto se denomina " feedforward" y sirve para mejorar aún más el rendimiento del seguimiento de referencia.
Una arquitectura de controlador de circuito cerrado común es el controlador PID .
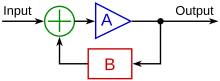
Circuito abierto y circuito cerrado
Básicamente, existen dos tipos de bucle de control: control de bucle abierto (feedforward) y control de bucle cerrado (feedback).

En el control de bucle abierto, la acción de control del controlador es independiente de la "salida del proceso" (o "variable de proceso controlada"). Un buen ejemplo de esto es una caldera de calefacción central controlada únicamente por un temporizador, de modo que se aplica calor durante un tiempo constante, independientemente de la temperatura del edificio. La acción de control es el encendido y apagado de la caldera, pero la variable controlada debería ser la temperatura del edificio, pero no es así porque se trata de un control de bucle abierto de la caldera, que no proporciona un control de bucle cerrado de la temperatura.
En el control de bucle cerrado, la acción de control del controlador depende de la salida del proceso. En el caso de la analogía de la caldera, esto incluiría un termostato para monitorear la temperatura del edificio y, por lo tanto, enviar una señal para garantizar que el controlador mantenga el edificio a la temperatura establecida en el termostato. Por lo tanto, un controlador de bucle cerrado tiene un bucle de retroalimentación que garantiza que el controlador ejerza una acción de control para proporcionar una salida de proceso que sea igual a la "entrada de referencia" o "punto de ajuste". Por este motivo, los controladores de bucle cerrado también se denominan controladores de retroalimentación. [3]
La definición de un sistema de control de lazo cerrado según la British Standards Institution es "un sistema de control que posee retroalimentación de monitoreo, siendo la señal de desviación formada como resultado de esta retroalimentación utilizada para controlar la acción de un elemento de control final de tal manera que tienda a reducir la desviación a cero". [4]
De igual modo, “Un sistema de control por retroalimentación es un sistema que tiende a mantener una relación prescrita de una variable del sistema con otra comparando funciones de estas variables y utilizando la diferencia como un medio de control”. [5]Función de transferencia de bucle cerrado
La salida del sistema y ( t ) se retroalimenta a través de una medición del sensor F para compararla con el valor de referencia r ( t ). El controlador C toma entonces el error e (diferencia) entre la referencia y la salida para cambiar las entradas u al sistema bajo control P . Esto se muestra en la figura. Este tipo de controlador es un controlador de bucle cerrado o controlador de retroalimentación.
Esto se denomina sistema de control de una sola entrada y una sola salida ( SISO ); los sistemas MIMO (es decir, Multi-Input-Multi-Output), con más de una entrada/salida, son comunes. En tales casos, las variables se representan mediante vectores en lugar de valores escalares simples. Para algunos sistemas de parámetros distribuidos, los vectores pueden ser de dimensión infinita (normalmente funciones).

Si asumimos que el controlador C , la planta P y el sensor F son lineales e invariantes en el tiempo (es decir, los elementos de su función de transferencia C ( s ), P ( s ) y F ( s ) no dependen del tiempo), los sistemas anteriores se pueden analizar utilizando la transformada de Laplace sobre las variables. Esto da las siguientes relaciones:
Resolviendo Y ( s ) en términos de R ( s ) obtenemos
La expresión se denomina función de transferencia de bucle cerrado del sistema. El numerador es la ganancia directa (de bucle abierto) de r a y , y el denominador es uno más la ganancia al pasar por el bucle de retroalimentación, la llamada ganancia de bucle. Si , es decir, tiene una norma grande con cada valor de s , y si , entonces Y ( s ) es aproximadamente igual a R ( s ) y la salida sigue de cerca la entrada de referencia.
Control de retroalimentación PID

Un controlador proporcional-integral-derivativo (controlador PID) es una técnica de control con mecanismo de retroalimentación de bucle de control ampliamente utilizada en sistemas de control.
Un controlador PID calcula continuamente un valor de error e ( t ) como la diferencia entre un punto de ajuste deseado y una variable de proceso medida y aplica una corrección basada en términos proporcionales , integrales y derivativos . PID es una sigla de Proporcional-Integral-Derivativo , que hace referencia a los tres términos que operan sobre la señal de error para producir una señal de control.
La comprensión teórica y la aplicación datan de la década de 1920 y se implementan en casi todos los sistemas de control analógicos; originalmente en controladores mecánicos, luego utilizando electrónica discreta y más tarde en computadoras de procesos industriales. El controlador PID es probablemente el diseño de control de retroalimentación más utilizado.
Si u ( t ) es la señal de control enviada al sistema, y ( t ) es la salida medida y r ( t ) es la salida deseada, y e ( t ) = r ( t ) − y ( t ) es el error de seguimiento, un controlador PID tiene la forma general
La dinámica de bucle cerrado deseada se obtiene ajustando los tres parámetros K P , K I y K D , a menudo de forma iterativa mediante "ajuste" y sin conocimientos específicos de un modelo de planta. A menudo, la estabilidad se puede asegurar utilizando únicamente el término proporcional. El término integral permite el rechazo de una perturbación de paso (a menudo una especificación sorprendente en el control de procesos ). El término derivativo se utiliza para proporcionar amortiguación o modelado de la respuesta. Los controladores PID son la clase de sistemas de control mejor establecida: sin embargo, no se pueden utilizar en varios casos más complicados, especialmente si se consideran sistemas MIMO .
La aplicación de la transformación de Laplace da como resultado la ecuación del controlador PID transformada
con la función de transferencia del controlador PID
Como ejemplo de ajuste de un controlador PID en el sistema de circuito cerrado H ( s ) , considere una planta de primer orden dada por
donde A y T P son algunas constantes. La salida de la planta se retroalimenta a través de
donde T F también es una constante. Ahora bien , si fijamos K D = KT D y podemos expresar la función de transferencia del controlador PID en forma de serie como
Al introducir P ( s ) , F ( s ) y C ( s ) en la función de transferencia de bucle cerrado H ( s ) , encontramos que al establecer
H ( s ) = 1. Con este ajuste en este ejemplo, la salida del sistema sigue exactamente la entrada de referencia.
Sin embargo, en la práctica, un diferenciador puro no es ni físicamente factible ni deseable [6] debido a la amplificación del ruido y los modos resonantes en el sistema. Por lo tanto, se utiliza en su lugar un enfoque de tipo compensador de adelanto de fase o un diferenciador con reducción gradual de paso bajo.
Referencias
- ^ Bechhoefer, John (31 de agosto de 2005). "Retroalimentación para físicos: un ensayo tutorial sobre control". Reseñas de Física Moderna . 77 (3): 783–836. doi :10.1103/RevModPhys.77.783.
- ^ Cao, FJ; Feito, M. (10 de abril de 2009). "Termodinámica de sistemas controlados por retroalimentación". Physical Review E . 79 (4): 041118. arXiv : 0805.4824 . doi :10.1103/PhysRevE.79.041118.
- ^ "Sistemas de control y retroalimentación" - JJ Di Steffano, AR Stubberud, IJ Williams. Serie de esquemas de Schaums, McGraw-Hill 1967
- ^ Mayr, Otto (1970). Los orígenes del control por retroalimentación . Clinton, MA, EE. UU.: The Colonial Press, Inc.
- ^ Mayr, Otto (1969). Los orígenes del control por retroalimentación . Clinton, MA, EE. UU.: The Colonial Press, Inc.
- ^ Ang, KH; Chong, GCY; Li, Y. (2005). "Análisis, diseño y tecnología de sistemas de control PID" (PDF) . IEEE Transactions on Control Systems Technology . 13 (4): 559–576. doi :10.1109/TCST.2005.847331. S2CID 921620. Archivado (PDF) desde el original el 13 de diciembre de 2013.
















