Polígono construible

En matemáticas , un polígono construible es un polígono regular que se puede construir con regla y compás . Por ejemplo, un pentágono regular se puede construir con regla y compás, mientras que un heptágono regular no. Hay una cantidad infinita de polígonos construibles, pero solo se conocen 31 con un número impar de lados.

Algunos polígonos regulares son fáciles de construir con compás y regla; otros no. Los antiguos matemáticos griegos sabían cómo construir un polígono regular con 3, 4 o 5 lados, ^{[1] : p. xi} y sabían cómo construir un polígono regular con el doble del número de lados de un polígono regular dado. ^{[1] : pp. 49–50} Esto llevó a plantear la pregunta: ¿es posible construir todos los polígonos regulares con compás y regla? Si no, ¿cuáles n -gonos (es decir, polígonos con n aristas) son construibles y cuáles no?

Carl Friedrich Gauss demostró la constructibilidad del polígono regular de 17 polígonos en 1796. Cinco años después, desarrolló la teoría de los periodos gaussianos en sus Disquisitiones Arithmeticae . Esta teoría le permitió formular una condición suficiente para la constructibilidad de los polígonos regulares. Gauss afirmó sin prueba que esta condición también era necesaria , ^[2] pero nunca publicó su prueba.

En 1837, Pierre Wantzel dio una prueba completa de la necesidad. El resultado se conoce como el teorema de Gauss-Wantzel : un n -gono regular se puede construir con compás y regla si y solo si n es el producto de una potencia de 2 y cualquier número de primos de Fermat distintos (desiguales) . Aquí, una potencia de 2 es un número de la forma , donde m ≥ 0 es un entero. Un primo de Fermat es un número primo de la forma , donde m ≥ 0 es un entero. El número de primos de Fermat involucrados puede ser 0, en cuyo caso n es una potencia de 2.${\estilo de visualización 2^{m}}$${\displaystyle 2^{(2^{m})}+1}$

Para reducir un problema geométrico a un problema de teoría de números pura , la prueba utiliza el hecho de que un n -gono regular es construible si y solo si el coseno es un número construible —es decir, puede escribirse en términos de las cuatro operaciones aritméticas básicas y la extracción de raíces cuadradas— . De manera equivalente, un n -gono regular es construible si cualquier raíz del n- ésimo polinomio ciclotómico es construible.${\displaystyle \cos(2\pi /n)}$

Reformulando el teorema de Gauss-Wantzel:

Un n -gono regular es construible con regla y compás si y sólo si n = 2 ^k p ₁ p ₂ ... p _t donde k y t son números enteros no negativos , y los p _i (cuando t > 0) son primos de Fermat distintos.

Los cinco primos de Fermat conocidos son:

F ₀ = 3, F ₁ = 5, F ₂ = 17, F ₃ = 257 y F ₄ = 65537 (secuencia A019434 en la OEIS ).

Dado que hay 31 subconjuntos no vacíos de los cinco primos de Fermat conocidos, hay 31 polígonos construibles conocidos con un número impar de lados.

Se sabe que los siguientes veintiocho números de Fermat, F ₅ a F ₃₂ , son compuestos . ^[3]

Por lo tanto, un n -gono regular es construible si

n = 3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 16 , 17 , 20 , 24 , 30 , 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257 , 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... (secuencia A003401 en la OEIS ),

mientras que un n -gono regular no es construible con compás y regla si

n = 7 , 9 , 11 , 13 , 14 , 18 , 19, 21, 22 , 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, 50, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 81, 82, 83, 84, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 97, 98, 99, 100, 101, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 126, 127, ... (secuencia A004169 en la OEIS ).

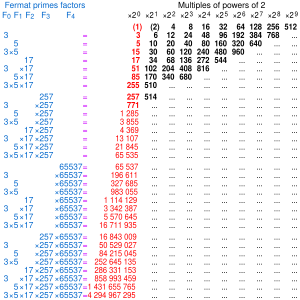
Como hay cinco primos de Fermat conocidos, conocemos 31 números que son productos de primos de Fermat distintos y, por lo tanto, 31 polígonos regulares de lados impares construibles. Estos son 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611 , 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 (secuencia A045544 en la OEIS ). Como comentó John Conway en El libro de los números , estos números, cuando se escriben en binario , son iguales a las primeras 32 filas del triángulo de Pascal módulo -2 , menos la fila superior, que corresponde a un monógono . (Debido a esto, los 1 en dicha lista forman una aproximación al triángulo de Sierpiński ). Este patrón se rompe después de esto, ya que el siguiente número de Fermat es compuesto (4294967297 = 641 × 6700417), por lo que las siguientes filas no corresponden a polígonos construibles. Se desconoce si existen más primos de Fermat y, por lo tanto, se desconoce cuántos polígonos regulares construibles de lados impares existen. En general, si hay q primos de Fermat, entonces hay 2 ^q −1 polígonos regulares construibles de lados impares .

A la luz de trabajos posteriores sobre la teoría de Galois , se han aclarado los principios de estas demostraciones. Es sencillo demostrar a partir de la geometría analítica que las longitudes construibles deben provenir de longitudes base mediante la solución de alguna secuencia de ecuaciones cuadráticas . ^[4] En términos de la teoría de campos , dichas longitudes deben estar contenidas en una extensión de campo generada por una torre de extensiones cuadráticas . De ello se deduce que un campo generado por construcciones siempre tendrá grado sobre el campo base que es una potencia de dos.

En el caso específico de un n -gono regular, la cuestión se reduce a la cuestión de construir una longitud

porque ​2π​/norte⁠ ,

que es un número trigonométrico y, por lo tanto, un número algebraico . Este número se encuentra en el n -ésimo cuerpo ciclotómico —y, de hecho, en su subcuerpo real , que es un cuerpo totalmente real y un espacio vectorial racional de dimensión

½ φ( n ),

donde φ( n ) es la función totiente de Euler . El resultado de Wantzel se reduce a un cálculo que muestra que φ( n ) es una potencia de 2 precisamente en los casos especificados.

En cuanto a la construcción de Gauss, cuando el grupo de Galois es un 2-grupo se deduce que tiene una secuencia de subgrupos de órdenes

1, 2, 4, 8, ...

que están anidados, cada uno en el siguiente (una serie de composición , en la terminología de la teoría de grupos ), algo simple de demostrar por inducción en este caso de un grupo abeliano . Por lo tanto, hay subcuerpos anidados dentro del cuerpo ciclotómico, cada uno de grado 2 sobre el anterior. Los generadores para cada uno de esos cuerpos se pueden escribir mediante la teoría de períodos de Gauss . Por ejemplo, para n  = 17 hay un período que es una suma de ocho raíces de la unidad , uno que es una suma de cuatro raíces de la unidad y uno que es la suma de dos, que es

porque ​2π​/17⁠ .

Cada una de ellas es una raíz de una ecuación cuadrática en función de la ecuación anterior. Además, estas ecuaciones tienen raíces reales en lugar de complejas , por lo que en principio pueden resolverse mediante una construcción geométrica: esto se debe a que todo el trabajo se realiza dentro de un campo totalmente real.

De esta manera el resultado de Gauss puede ser entendido en términos actuales; para el cálculo real de las ecuaciones a resolver, los periodos pueden ser elevados al cuadrado y comparados con los periodos 'inferiores', en un algoritmo bastante factible.

Se conocen construcciones con regla y compás para todos los polígonos construibles conocidos. Si n  =  pq con p  = 2 o p y q son coprimos , se puede construir un n -gono a partir de un p -gono y un q -gono.

• Si p  = 2, se traza un q -gono y se biseca uno de sus ángulos centrales. A partir de esto, se puede construir un 2 q -gono.
• Si p  > 2, inscríbase un p -gono y un q -gono en la misma circunferencia de manera que compartan un vértice. Como p y q son coprimos, existen números enteros a y b tales que ap + bq = 1. Entonces 2 a π/ q + 2 b π/ p = 2π/ pq . A partir de esto, se puede construir un pq -gono.

Por lo tanto, sólo hay que encontrar una construcción con regla y compás para n -gonos donde n es un primo de Fermat.

• La construcción de un triángulo equilátero es sencilla y se conoce desde la antigüedad ; véase Triángulo equilátero .
• Las construcciones del pentágono regular fueron descritas tanto por Euclides ( Elementos , ca. 300 a. C.) como por Ptolomeo ( Almagesto , ca. 150 d. C.).
• Aunque Gauss demostró que el 17-gono regular es construible, no mostró cómo hacerlo. La primera construcción se debe a Erchinger, unos años después del trabajo de Gauss.
• Las primeras construcciones explícitas de un 257-gono regular fueron dadas por Magnus Georg Paucker (1822) ^[5] y Friedrich Julius Richelot (1832). ^[6]
• Johann Gustav Hermes (1894) fue el primero en proponer una construcción para un 65537-gono regular . La construcción es muy compleja; Hermes pasó diez años completando el manuscrito de 200 páginas. ^[7]

De izquierda a derecha, construcciones de un 15-gono , 17-gono , 257-gono y 65537-gono . Solo se muestra la primera etapa de la construcción de 65537-gono; las construcciones de los 15-gonos, 17-gonos y 257-gonos se dan completas.

El concepto de constructibilidad que se analiza en este artículo se aplica específicamente a las construcciones con regla y compás . Si se permiten otras herramientas, se pueden realizar más construcciones. Las llamadas construcciones de neusis , por ejemplo, utilizan una regla marcada . Las construcciones son una idealización matemática y se supone que se realizan con exactitud.

Un polígono regular con n lados se puede construir con regla, compás y trisectriz de ángulos si y solo si donde r, s, k ≥ 0 y donde los p _i son primos de Pierpont distintos mayores que 3 (primos de la forma ^{[8] : Teoría 2} Estos polígonos son exactamente los polígonos regulares que se pueden construir con Sección cónica , y los polígonos regulares que se pueden construir con Plegado de papel . Los primeros números de lados de estos polígonos son:${\displaystyle n=2^{r}3^{s}p_{1}p_{2}\cdots p_{k},}$${\displaystyle 2^{t}3^{u}+1).}$

3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 24, 26, 27, 28, 30, 32, 34, 35, 36, 37, 38, 39, 40, 42, 45, 48, 51, 52, 54, 56, 57, 60, 63, 64, 65, 68, 70, 72, 73, 74, 76, 78, 80, 81, 84, 85, 90, 91, 95, 96, 97, 102, 104, 105, 108, 109, 111, 112, 114, 117, 119, 120, 126, 128, 130, 133, 135, 136, 140, 144, 146, 148, 152, 153, 156, 160, 162, 3, 168, 170, 171, 180, 182, 185, 189, 190, 192, 193, 194, 195, 204, 208, 210, 216, 218, 219, 221, 222, 224, 228, 234, 238, 240, 243, 247, 252, 255, 256, 257, 259, 260, 266, 270, 272, 273, 280, 285, 288, 291, 292, 296, ... (secuencia A122254 en la OEIS )

• Polígono
• Círculo de Carlyle

• Duane W. DeTemple (1991). "Círculos de Carlyle y la simplicidad de Lemoine en construcciones poligonales". The American Mathematical Monthly . 98 (2): 97–108. doi :10.2307/2323939. JSTOR  2323939. MR  1089454.
• Christian Gottlieb (1999). "La construcción simple y directa del 257-gono regular". Mathematical Intelligencer . 21 (1): 31–37. doi :10.1007/BF03024829. MR  1665155. S2CID  123567824.
• Fórmulas de polígonos regulares, preguntas frecuentes del Dr. Math.
• Carl Schick: Weiche Primzahlen und das 257-Eck: eine analytische Lösung des 257-Ecks. Zúrich: C. Schick, 2008. ISBN 978-3-9522917-1-9 . 
• 65537-gon, construcción exacta para el primer lado, utilizando la Cuadratriz de Hipias y GeoGebra como ayudas adicionales, con breve descripción (alemán)