Número de Stokes

El número de Stokes ( Stk ), llamado así por George Gabriel Stokes , es un número adimensional que caracteriza el comportamiento de las partículas suspendidas en un flujo de fluido . El número de Stokes se define como la relación entre el tiempo característico de una partícula (o gota ) y un tiempo característico del flujo o de un obstáculo, o

${\displaystyle \mathrm {Stk} ={\frac {t_{0}\,u_{0}}{l_{0}}}}$

donde es el tiempo de relajación de la partícula (la constante de tiempo en la disminución exponencial de la velocidad de la partícula debido al arrastre), es la velocidad del fluido del flujo bien alejado del obstáculo, y es la dimensión característica del obstáculo (normalmente su diámetro) o una escala de longitud característica en el flujo (como el espesor de la capa límite). ^[1] Una partícula con un número de Stokes bajo sigue las líneas de corriente del fluido ( advección perfecta ), mientras que una partícula con un número de Stokes grande está dominada por su inercia y continúa a lo largo de su trayectoria inicial.${\estilo de visualización t_{0}}$${\displaystyle u_{0}}$${\displaystyle l_{0}}$

En el caso del flujo de Stokes , que es cuando el número de Reynolds de la partícula (o gota) es menor que aproximadamente uno, el coeficiente de arrastre de la partícula es inversamente proporcional al propio número de Reynolds. En ese caso, el tiempo característico de la partícula se puede escribir como

${\displaystyle t_{0}={\frac {\rho _{p}d_{p}^{2}}{18\mu _{g}}}}$

donde es la densidad de partículas , es el diámetro de partículas y es la viscosidad dinámica del fluido . ^[2]${\displaystyle \rho_{p}}$$estilo de visualización d_{p}}$${\displaystyle \mu_{g}}$

En dinámica de fluidos experimental, el número de Stokes es una medida de la fidelidad del trazador de flujo en experimentos de velocimetría de imágenes de partículas (PIV) donde partículas muy pequeñas son arrastradas en flujos turbulentos y observadas ópticamente para determinar la velocidad y dirección del movimiento del fluido (también conocido como el campo de velocidad del fluido). Para una precisión de rastreo aceptable, el tiempo de respuesta de la partícula debe ser más rápido que la escala de tiempo más pequeña del flujo. Los números de Stokes más pequeños representan una mejor precisión de rastreo; para , las partículas se desprenderán de un flujo especialmente cuando el flujo se desacelera abruptamente. Para , las partículas siguen de cerca las líneas de corriente del fluido. Si , los errores de precisión de rastreo son inferiores al 1%. ^[3]${\displaystyle \mathrm {Stk} \gg 1}$${\displaystyle \mathrm {Estilo} \ll 1}$${\displaystyle \mathrm {Stk} <0.1}$

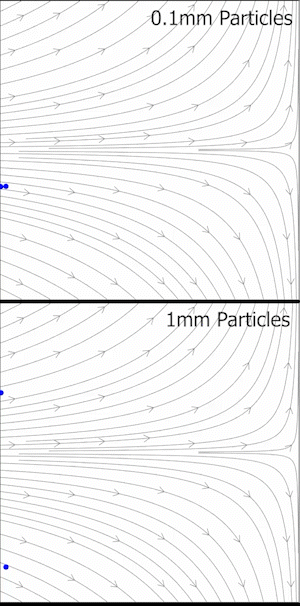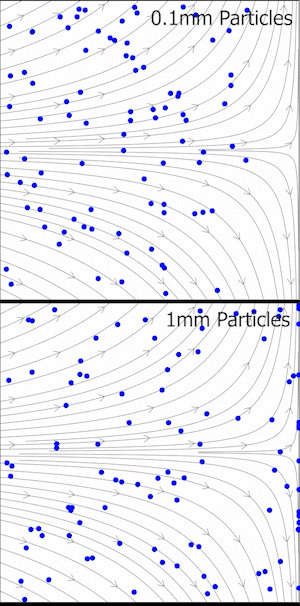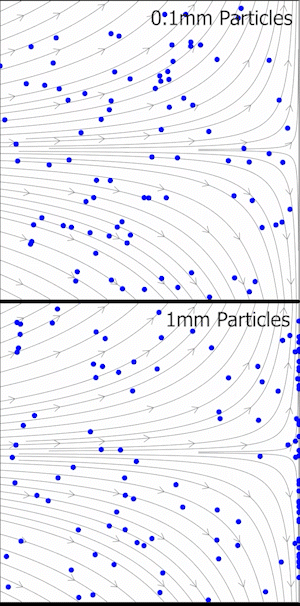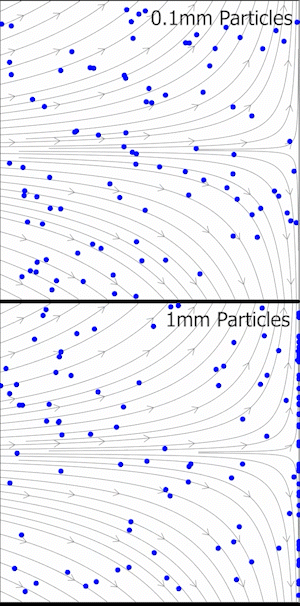
El número de Stokes proporciona un medio para estimar la calidad de los conjuntos de datos PIV, como se explicó anteriormente. Sin embargo, es posible que no sea evidente una definición de una escala de longitud o velocidad característica en todas las aplicaciones. Por lo tanto, se podría obtener una idea más profunda de cómo surge un retraso de seguimiento simplemente definiendo las ecuaciones diferenciales de una partícula en el régimen de Stokes. Una partícula que se mueve con el fluido a cierta velocidad se encontrará con un campo de velocidad de fluido variable a medida que se desplaza. Supongamos que la velocidad del fluido, en el marco de referencia lagrangiano de la partícula, es . Es la diferencia entre estas velocidades la que generará la fuerza de arrastre necesaria para corregir la trayectoria de la partícula:$estilo de visualización v_{p}(t)}$$Estilo de visualización vf(t)$

${\displaystyle \Delta v(t)=v_{f}(t)-v_{p}(t)}$

La fuerza de arrastre de Stokes es entonces:

${\displaystyle F_{D}=3\pi \mu d_{p}\Delta v}$

La masa de la partícula es:

${\displaystyle m_{p}=\rho _{p}{\frac {4}{3}}\pi {\bigg (}{\frac {d_{p}}{2}}{\bigg )}^{3}=\rho _{p}{\frac {\pi d_{p}^{3}}{6}}}$

Por tanto, la aceleración de la partícula se puede encontrar a través de la segunda ley de Newton:

${\displaystyle {\frac {dv_{p}(t)}{dt}}={\frac {F_{D}}{m_{p}}}={\frac {18\mu}{{d_{p}}^{2}\rho _{p}}}\Delta v(t)}$

Tenga en cuenta que el tiempo de relajación se puede reemplazar para obtener:${\displaystyle t_{0}={\frac {\rho _{p}d_{p}^{2}}{18\mu _{g}}}}$

${\displaystyle {\frac {dv_{p}(t)}{dt}}={\frac {1}{t_{0}}}\Delta v(t)}$

La ecuación diferencial de primer orden anterior se puede resolver mediante el método de la transformada de Laplace :

${\displaystyle t_{0}sv_{p}(s)=v_{f}-v_{p}(s)}$

${\displaystyle {\frac {v_{p}(s)}{v_{f}(s)}}={\frac {1}{t_{0}s+1}}}$

La solución anterior, en el dominio de la frecuencia, caracteriza un sistema de primer orden con un tiempo característico de . Por lo tanto, la frecuencia de ganancia (corte) de −3 dB será:${\estilo de visualización t_{0}}$

${\displaystyle f_{-3{\text{ dB}}}={\frac {1}{2\pi t_{0}}}}$

La frecuencia de corte y la función de transferencia de partículas, graficadas en el panel lateral, permiten evaluar el error de PIV en aplicaciones de flujo inestable y su efecto sobre las cantidades espectrales de turbulencia y la energía cinética.

El error de sesgo en el seguimiento de partículas analizado en la sección anterior es evidente en el dominio de la frecuencia, pero puede ser difícil de apreciar en los casos en los que se realiza un seguimiento del movimiento de la partícula para realizar mediciones del campo de flujo (como en la velocimetría de imágenes de partículas ). Una solución simple pero perspicaz para la ecuación diferencial mencionada anteriormente es posible cuando la función de fuerza es una función escalonada de Heaviside; que representa partículas que pasan por una onda de choque. En este caso, es la velocidad del flujo aguas arriba del choque; mientras que es la caída de velocidad a través del choque.${\displaystyle v_{f}(t)=V_{u}-\Delta VH(t)}$${\displaystyle V_{u}}$${\displaystyle \Delta V}$

La respuesta al escalón de una partícula es una exponencial simple:

${\displaystyle v_{p}(t)=(V_{u}-\Delta V)+\Delta Ve^{-t/t_{0}}}$

Para convertir la velocidad en función del tiempo a una distribución de velocidad de partículas en función de la distancia, supongamos un salto de velocidad unidimensional en la dirección. Supongamos que está posicionada donde está la onda de choque y luego integremos la ecuación anterior para obtener:${\estilo de visualización x}$${\displaystyle x=0}$

${\displaystyle x_{\text{partícula}}=\int _{0}^{\Delta t}v_{p}(t)dt=\int _{0}^{\Delta t}(V_{u}-\Delta V)dt+\int _{0}^{\Delta t}\Delta Ve^{-t/t_{0}}dt}$

${\displaystyle x_{\text{partícula}}=\Delta t(V_{u}-\Delta V)+\Delta t\Delta V(1-e^{-\Delta t/t_{0}})}$

Considerando un tiempo de relajación de (tiempo hasta el cambio de velocidad del 95%), tenemos:${\displaystyle \Delta t=3t_{0}}$

${\displaystyle x_{{\text{partícula}},95\%}=3t_{0}(V_{u}-\Delta V)+3t_{0}\Delta V(1-e^{-3}) }$

${\displaystyle x_{{\text{partícula}},95\%}=3t_{0}(V_{u}-0.05\Delta V)}$

Esto significa que la velocidad de la partícula se estabilizaría en un 5 % de la velocidad descendente desde el choque. En la práctica, esto significa que una onda de choque se vería borrosa en un sistema PIV aproximadamente a esta distancia. ${\displaystyle x_{{\text{partícula}},95\%}}$${\displaystyle x_{{\text{partícula}},95\%}}$

Por ejemplo, considere una onda de choque normal de número de Mach a una temperatura de estancamiento de 298 K. Una partícula de propilenglicol de desdibujaría el flujo en ; mientras que a desdibujaría el flujo en (lo que, en la mayoría de los casos, produciría resultados PIV inaceptables).${\estilo de visualización M=2}$${\displaystyle d_{p}=1~\mu {\text{m}}}$${\displaystyle x_{{\text{partícula}},95\%}=5{\text{ mm}}}$${\displaystyle d_{p}=10~\mu {\text{m}}}$${\displaystyle x_{{\text{partícula}},95\%}=500{\text{ mm}}}$

Aunque una onda de choque es el peor escenario de desaceleración abrupta de un flujo, ilustra el efecto del error de seguimiento de partículas en PIV, que da como resultado una difuminación de los campos de velocidad adquiridos en escalas de longitud de orden .${\displaystyle x_{{\text{partícula}},95\%}}$

El análisis precedente no será preciso en el régimen ultra-stokesiano, es decir, si el número de Reynolds de la partícula es mucho mayor que la unidad. Suponiendo un número de Mach mucho menor que la unidad, Israel y Rosner demostraron una forma generalizada del número de Stokes. ^[4]

$${\displaystyle {\text{Stk}}_{\text{e}}={\text{Stk}}{\frac {24}{{\text{Re}}_{o}}}\int _{0}^{{\text{Re}}_{o}}{\frac {d{\text{Re}}^{\prime }}{C_{D}({\text{Re}}^{\prime }){\text{Re}}^{\prime }}}}$$

¿Dónde está el "número de Reynolds de corriente libre de partículas"?${\displaystyle {\text{Re}}_{o}}$

$${\displaystyle {\text{Re}}_{o}={\frac {\rho _{g}|\mathbf {u} |d_{p}}{\mu _{g}}}}$$

Se definió una función adicional mediante ^[4] que describe el factor de corrección de arrastre no Stokesiano,${\displaystyle \psi ({\text{Re}}_{o})}$

$${\displaystyle {\text{Stk}}_{e}={\text{Stk}}\cdot \psi ({\text{Re}}_{o})}$$

De ello se deduce que esta función está definida por,

$${\displaystyle \psi ({\text{Re}}_{o})={\frac {24}{{\text{Re}}_{o}}}\int _{0}^{{\text{Re}}_{o}}{\frac {d{\text{Re}}^{\prime }}{C_{D}({\text{Re}}^{\prime }){\text{Re}}^{\prime }}}}$$

Considerando los números de Reynolds de flujo libre de partículas limitantes, como entonces y por lo tanto . Por lo tanto, como se esperaba, el factor de corrección es la unidad en el régimen de arrastre de Stokes. Wessel y Righi ^[5] evaluaron a partir de la correlación empírica para el arrastre en una esfera de Schiller y Naumann. ^[6]${\displaystyle {\text{Re}}_{o}\to 0}$${\displaystyle C_{D}({\text{Re}}_{o})\to 24/{\text{Re}}_{o}}$${\displaystyle \psi \to 1}$${\displaystyle \psi }$${\displaystyle C_{D}({\text{Re}})}$

$${\displaystyle \psi ({\text{Re}}_{o})={\frac {3({\sqrt {c}}{\text{Re}}_{o}^{1/3}-\arctan({\sqrt {c}}{\text{Re}}_{o}^{1/3}))}{c^{3/2}{\text{Re}}_{o}}}}$$

Donde la constante . El número de Stokes convencional subestimará significativamente la fuerza de arrastre para los números de Reynolds de flujo libre de partículas grandes. Por lo tanto, sobrestimará la tendencia de las partículas a desviarse de la dirección del flujo del fluido. Esto conducirá a errores en los cálculos posteriores o en las comparaciones experimentales.${\displaystyle c=0.158}$

Por ejemplo, la captura selectiva de partículas mediante una boquilla circular alineada de paredes delgadas está dada por Belyaev y Levin ^[7] como:

${\displaystyle c/c_{0}=1+(u_{0}/u-1)\left(1-{\frac {1}{1+\mathrm {Stk} (2+0.617u/u_{0})}}\right)}$

donde es la concentración de partículas, es la velocidad y el subíndice 0 indica condiciones muy arriba de la boquilla. La distancia característica es el diámetro de la boquilla. Aquí se calcula el número de Stokes,${\displaystyle c}$${\displaystyle u}$

${\displaystyle \mathrm {Stk} ={\frac {u_{0}V_{s}}{dg}}}$

donde es la velocidad de sedimentación de la partícula, es el diámetro interior del tubo de muestreo y es la aceleración de la gravedad.${\displaystyle V_{s}}$${\displaystyle d}$${\displaystyle g}$

• Ley de Stokes – Para la fuerza de arrastre en fluidos sobre partículas cuyo número de Reynolds es menor que uno ^[8]

• Fuchs, NA (1989). La mecánica de los aerosoles . Nueva York: Dover Publications. ISBN 978-0-486-66055-4.
• Hinds, William C. (1999). Tecnología de aerosoles: propiedades, comportamiento y medición de partículas en suspensión en el aire . Nueva York: Wiley. ISBN 978-0-471-19410-1.
• Snyder, WH; Lumley, JL (1971). "Algunas mediciones de funciones de autocorrelación de velocidad de partículas en un flujo turbulento". Journal of Fluid Mechanics . 48 : 41–71. Bibcode :1971JFM....48...41S. doi :10.1017/S0022112071001460. S2CID  122731370.
• Collins, LR; Keswani, A (2004). "Escalamiento del número de Reynolds de la agrupación de partículas en aerosoles turbulentos". New Journal of Physics . 6 (119): 119. Bibcode :2004NJPh....6..119C. doi : 10.1088/1367-2630/6/1/119 .