Hacer un pedido

Relaciones binarias transitivas en a mi
Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Total, Semiconnex Anti- reflexivo Relación de equivalencia Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado (cuasi pedido) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Orden parcial ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Pedido anticipado total ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Pedido total ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Pedido previo al pozo ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Bien-cuasi-ordenamiento ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Buen orden ✗ Y Y Y ✗ ✗ Y ✗ ✗ Enrejado ✗ Y ✗ ✗ Y Y Y ✗ ✗ Unión de semirrejilla ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Conocer-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Orden parcial estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden débil estricta ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Orden total estricta ✗ Y Y ✗ ✗ ✗ ✗ Y Y Simétrico Antisimétrico Conectado Bien fundado Tiene uniones Tiene cumple Reflexivo Irreflexivo Asimétrico Definiciones, para todos y${\estilo de visualización a,b}$${\displaystyle S\neq \varnothing :}$ ${\displaystyle {\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}aRb{\text{ y }}&bRa\\\Rightarrow a={}&b\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ o }}&bRa\end{aligned}}}$ ${\displaystyle {\begin{aligned}\min S\\{\text{existe}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\vee b\\{\text{existe}}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a\wedge b\\{\text{existe}}\end{aligned}}}$ ${\estilo de visualización aRa}$ ${\displaystyle {\text{no }}aRa}$ ${\displaystyle {\begin{aligned}aRb\Rightarrow \\{\text{no }}bRa\end{aligned}}}$
Yindica que la propiedad de la columna siempre es verdadera para el término de la fila (a la izquierda), mientras que ✗ indica que la propiedad no está garantizada en general (puede cumplirse o no). Por ejemplo, que toda relación de equivalencia es simétrica, pero no necesariamente antisimétrica, se indica con en la columna "Simétrica" ​​y ✗ en la columna "Antisimétrica", respectivamente.Y Todas las definiciones requieren tácitamente que la relación homogénea sea transitiva : para todo si y entonces La definición de un término puede requerir propiedades adicionales que no están incluidas en esta tabla.${\estilo de visualización R}$${\estilo de visualización a,b,c,}$$Estilo de visualización aRb$${\estilo de visualización bRc}$${\estilo de visualización aRc.}$

En matemáticas , especialmente en la teoría del orden , un preorden o cuasiorden es una relación binaria que es reflexiva y transitiva . El nombre preorden pretende sugerir que los preórdenes son órdenes casi parciales , pero no del todo, ya que no son necesariamente antisimétricos .

Un ejemplo natural de un preorden es la relación divisoria "x divide a y" entre números enteros, polinomios o elementos de un anillo conmutativo . Por ejemplo, la relación divisoria es reflexiva, ya que cada número entero se divide a sí mismo. Pero la relación divisoria no es antisimétrica, porque divide y divide . Es a este preorden al que se refieren "mayor" y "menor" en las frases " máximo común divisor " y " mínimo común múltiplo " (excepto que, para los números enteros, el máximo común divisor es también el mayor para el orden natural de los números enteros). ${\estilo de visualización 1}$${\estilo de visualización -1}$${\estilo de visualización -1}$${\estilo de visualización 1}$

Los preórdenes están estrechamente relacionados con las relaciones de equivalencia y los órdenes parciales (no estrictos). Ambos son casos especiales de un preorden: un preorden antisimétrico es un orden parcial y un preorden simétrico es una relación de equivalencia. Además, un preorden en un conjunto puede definirse de manera equivalente como una relación de equivalencia en , junto con un orden parcial en el conjunto de la clase de equivalencia. Al igual que los órdenes parciales y las relaciones de equivalencia, los preórdenes (en un conjunto no vacío) nunca son asimétricos .${\estilo de visualización X}$${\estilo de visualización X}$

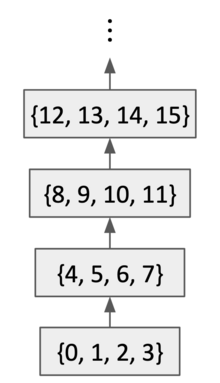
Un preorden puede visualizarse como un grafo dirigido , con elementos del conjunto correspondientes a vértices, y la relación de orden entre pares de elementos correspondientes a las aristas dirigidas entre vértices. Lo inverso no es cierto: la mayoría de los grafos dirigidos no son ni reflexivos ni transitivos. Un preorden que es antisimétrico ya no tiene ciclos; es un orden parcial y corresponde a un grafo acíclico dirigido . Un preorden que es simétrico es una relación de equivalencia; se puede pensar que ha perdido los marcadores de dirección en las aristas del grafo. En general, el grafo dirigido correspondiente de un preorden puede tener muchos componentes desconectados.

Como relación binaria, un preorden puede denotarse como o . En palabras, cuando se puede decir que b cubre a o que a precede a b , o que b se reduce a a . Ocasionalmente, también se utiliza la notación ← o → .${\displaystyle \,\lesssim \,}$${\estilo de visualización \,\leq \,}$${\displaystyle a\lessim b,}$

Sea una relación binaria en un conjunto tal que por definición, es algún subconjunto de y se utiliza la notación en lugar de Entonces se llama preorden o cuasiorden si es reflexivo y transitivo ; es decir, si satisface:${\displaystyle \,\lesssim \,}$ ${\estilo de visualización P,}$${\displaystyle \,\lesssim \,}$${\displaystyle P\times P}$${\displaystyle a\lessim b}$${\displaystyle (a,b)\in \,\lesssim .}$${\displaystyle \,\lesssim \,}$

1. Reflexividad : para todos y${\displaystyle a\lesssim a}$${\displaystyle a\en P,}$
2. Transitividad : si para todos${\displaystyle a\lesssim b{\text{ and }}b\lesssim c{\text{ then }}a\lesssim c}$${\displaystyle a,b,c\in P.}$

Un conjunto que está equipado con un preorden se llama conjunto preordenado (o proconjunto ). ^[1]

Dado un preorden en uno, se puede definir una relación de equivalencia en tal que La relación resultante es reflexiva ya que el preorden es reflexivo; transitiva al aplicar la transitividad de dos veces; y simétrica por definición. ${\displaystyle \,\lesssim \,}$${\displaystyle S}$ ${\displaystyle \,\sim \,}$${\displaystyle S}$$${\displaystyle a\sim b\quad {\text{ if and only if }}\quad a\lesssim b\;{\text{ and }}\;b\lesssim a.}$$${\displaystyle \,\sim \,}$${\displaystyle \,\lesssim \,}$${\displaystyle \,\lesssim \,}$

Usando esta relación, es posible construir un orden parcial sobre el conjunto cociente de la equivalencia, que es el conjunto de todas las clases de equivalencia de Si el preorden se denota por entonces es el conjunto de - clases de equivalencia de ciclo : si y solo si o está en un -ciclo con . En cualquier caso, en es posible definir si y solo si Que esto está bien definido, es decir, que su condición definitoria no depende de qué representantes de y se elijan, se sigue de la definición de Se verifica fácilmente que esto produce un conjunto parcialmente ordenado.${\displaystyle S/\sim ,}$${\displaystyle \,\sim .}$${\displaystyle R^{+=},}$${\displaystyle S/\sim }$${\displaystyle R}$${\displaystyle x\in [y]}$${\displaystyle x=y}$${\displaystyle x}$${\displaystyle R}$${\displaystyle y}$${\displaystyle S/\sim }$${\displaystyle [x]\leq [y]}$${\displaystyle x\lesssim y.}$${\displaystyle [x]}$${\displaystyle [y]}$${\displaystyle \,\sim .\,}$

A la inversa, a partir de cualquier orden parcial de una partición de un conjunto es posible construir un preorden sobre sí mismo. Existe una correspondencia biunívoca entre preórdenes y pares (partición, orden parcial).${\displaystyle S,}$${\displaystyle S}$

Ejemplo : Sea una teoría formal , que es un conjunto de oraciones con ciertas propiedades (cuyos detalles se pueden encontrar en el artículo sobre el tema ). Por ejemplo, podría ser una teoría de primer orden (como la teoría de conjuntos de Zermelo-Fraenkel ) o una teoría de orden cero más simple . Una de las muchas propiedades de es que está cerrada bajo consecuencias lógicas de modo que, por ejemplo, si una oración implica lógicamente alguna oración que se escribirá como y también como entonces necesariamente (por modus ponens ). La relación es un preorden en porque siempre se cumple y siempre que y ambos se cumplen entonces también lo hace Además, para cualquier si y solo si ; es decir, dos oraciones son equivalentes con respecto a si y solo si son lógicamente equivalentes . Esta relación de equivalencia particular se denota comúnmente con su propio símbolo especial y, por lo tanto, este símbolo puede usarse en lugar de La clase de equivalencia de una oración denotada por consiste en todas las oraciones que son lógicamente equivalentes a (es decir, todas tales que ). El orden parcial inducido por el cual también se denotará por el mismo símbolo se caracteriza por si y solo si donde la condición del lado derecho es independiente de la elección de representantes y de las clases de equivalencia. Todo lo que se ha dicho hasta ahora también se puede decir de su relación inversa El conjunto preordenado es un conjunto dirigido porque si y si denota la oración formada por la conjunción lógica entonces y donde El conjunto parcialmente ordenado es, en consecuencia, también un conjunto dirigido. Véase el álgebra de Lindenbaum-Tarski para un ejemplo relacionado.${\displaystyle S}$${\displaystyle S}$${\displaystyle S}$${\displaystyle A\in S}$${\displaystyle B,}$${\displaystyle A\Rightarrow B}$${\displaystyle B\Leftarrow A,}$${\displaystyle B\in S}$${\displaystyle \,\Leftarrow \,}$${\displaystyle S}$${\displaystyle A\Leftarrow A}$${\displaystyle A\Leftarrow B}$${\displaystyle B\Leftarrow C}$${\displaystyle A\Leftarrow C.}$${\displaystyle A,B\in S,}$ ${\displaystyle A\sim B}$${\displaystyle A\Leftarrow B{\text{ and }}B\Leftarrow A}$${\displaystyle \,\Leftarrow \,}$${\displaystyle A\sim B}$${\displaystyle A\iff B,}$${\displaystyle \,\iff \,}$${\displaystyle \,\sim .}$${\displaystyle A,}$${\displaystyle [A],}$${\displaystyle B\in S}$${\displaystyle A}$${\displaystyle B\in S}$${\displaystyle A\iff B}$${\displaystyle S/\sim }$${\displaystyle \,\Leftarrow ,\,}$${\displaystyle \,\Leftarrow ,\,}$${\displaystyle [A]\Leftarrow [B]}$${\displaystyle A\Leftarrow B,}$${\displaystyle A\in [A]}$${\displaystyle B\in [B]}$${\displaystyle \,\Leftarrow \,}$ ${\displaystyle \,\Rightarrow .\,}$${\displaystyle (S,\Leftarrow )}$${\displaystyle A,B\in S}$${\displaystyle C:=A\wedge B}$ ${\displaystyle \,\wedge ,\,}$${\displaystyle A\Leftarrow C}$${\displaystyle B\Leftarrow C}$${\displaystyle C\in S.}$${\displaystyle \left(S/\sim ,\Leftarrow \right)}$

Si se reemplaza la reflexividad por la irreflexividad (manteniendo la transitividad), obtenemos la definición de un orden parcial estricto en . Por este motivo, a veces se utiliza el término preorden estricto para un orden parcial estricto. Es decir, se trata de una relación binaria en que satisface:${\displaystyle P}$${\displaystyle \,<\,}$${\displaystyle P}$

1. Irreflexividad o antirreflexividad: no para todo lo que es, es falso para todo y${\displaystyle a<a}$${\displaystyle a\in P;}$${\displaystyle \,a<a}$${\displaystyle a\in P,}$
2. Transitividad : si para todos${\displaystyle a<b{\text{ and }}b<c{\text{ then }}a<c}$${\displaystyle a,b,c\in P.}$

Cualquier preorden da lugar a un orden parcial estricto definido por si y solo si y no . Usando la relación de equivalencia introducida anteriormente, si y solo si y por lo tanto se cumple lo siguiente La relación es un orden parcial estricto y cada orden parcial estricto se puede construir de esta manera. Si el preorden es antisimétrico (y por lo tanto un orden parcial) entonces la equivalencia es igualdad (es decir, si y solo si ) y por lo tanto en este caso, la definición de se puede reformular como: Pero lo que es más importante, esta nueva condición no se usa como (ni es equivalente a) la definición general de la relación (es decir, no se define como: si y solo si ) porque si el preorden no es antisimétrico entonces la relación resultante no sería transitiva (considere cómo se relacionan los elementos no iguales equivalentes). Esta es la razón para usar el símbolo " " en lugar del símbolo "menor o igual a" " ", que podría causar confusión para un preorden que no es antisimétrico ya que podría sugerir engañosamente que implica${\displaystyle \,\lesssim \,}$${\displaystyle a<b}$${\displaystyle a\lesssim b}$${\displaystyle b\lesssim a}$${\displaystyle \,\sim \,}$${\displaystyle a<b}$${\displaystyle a\lesssim b{\text{ and not }}a\sim b;}$$${\displaystyle a\lesssim b\quad {\text{ if and only if }}\quad a<b\;{\text{ or }}\;a\sim b.}$$${\displaystyle \,<\,}$${\displaystyle \,\lesssim \,}$${\displaystyle \,\sim \,}$${\displaystyle a\sim b}$${\displaystyle a=b}$${\displaystyle \,<\,}$$${\displaystyle a<b\quad {\text{ if and only if }}\quad a\lesssim b\;{\text{ and }}\;a\neq b\quad \quad ({\text{assuming }}\lesssim {\text{ is antisymmetric}}).}$$${\displaystyle \,<\,}$${\displaystyle \,<\,}$${\displaystyle a<b}$${\displaystyle a\lesssim b{\text{ and }}a\neq b}$${\displaystyle \,\lesssim \,}$${\displaystyle \,<\,}$${\displaystyle \lesssim }$${\displaystyle \leq }$${\displaystyle a\leq b}$${\displaystyle a<b{\text{ or }}a=b.}$

Usando la construcción anterior, múltiples preórdenes no estrictos pueden producir el mismo preorden estricto , por lo que sin más información sobre cómo se construyó (tal conocimiento de la relación de equivalencia , por ejemplo), podría no ser posible reconstruir el preorden no estricto original a partir de Los posibles preórdenes (no estrictos) que inducen el preorden estricto dado incluyen los siguientes:${\displaystyle \,<,\,}$${\displaystyle \,<\,}$${\displaystyle \,\sim \,}$${\displaystyle \,<.\,}$${\displaystyle \,<\,}$

• Definir como (es decir, tomar el cierre reflexivo de la relación). Esto da el orden parcial asociado con el orden parcial estricto " " a través del cierre reflexivo; en este caso la equivalencia es igualdad, por lo que los símbolos y no son necesarios.${\displaystyle a\leq b}$${\displaystyle a<b{\text{ or }}a=b}$${\displaystyle <}$${\displaystyle \,=,}$${\displaystyle \,\lesssim \,}$${\displaystyle \,\sim \,}$
• Definir como " " (es decir, tomar el complemento inverso de la relación), lo que corresponde a definir como "ninguno "; estas relaciones y son en general no transitivas; sin embargo, si lo son entonces es una equivalencia; en ese caso " " es un orden débil estricto . El preorden resultante es conexo (antes llamado total); es decir, un preorden total .${\displaystyle a\lesssim b}$${\displaystyle {\text{ not }}b<a}$${\displaystyle a\sim b}$${\displaystyle a<b{\text{ nor }}b<a}$${\displaystyle \,\lesssim \,}$${\displaystyle \,\sim \,}$${\displaystyle \,\sim \,}$${\displaystyle <}$

Si entonces El recíproco se cumple (es decir, ) si y sólo si siempre que entonces o${\displaystyle a\leq b}$${\displaystyle a\lesssim b.}$${\displaystyle \,\lesssim \;\;=\;\;\leq \,}$${\displaystyle a\neq b}$${\displaystyle a<b}$${\displaystyle b<a.}$

• La relación de alcanzabilidad en cualquier grafo dirigido (que posiblemente contenga ciclos) da lugar a un preorden, donde en el preorden si y solo si hay un camino de x a y en el grafo dirigido. A la inversa, cada preorden es la relación de alcanzabilidad de un grafo dirigido (por ejemplo, el grafo que tiene una arista de x a y para cada par ( x , y ) con ). Sin embargo, muchos grafos diferentes pueden tener el mismo preorden de alcanzabilidad entre sí. De la misma manera, la alcanzabilidad de grafos acíclicos dirigidos , grafos dirigidos sin ciclos, da lugar a conjuntos parcialmente ordenados (preórdenes que satisfacen una propiedad de antisimetría adicional).${\displaystyle x\lesssim y}$${\displaystyle x\lesssim y}$
• La relación grafo-menor también es un preorden.

En informática se pueden encontrar ejemplos de los siguientes preórdenes.

• El orden asintótico produce un preordenamiento de las funciones . La relación de equivalencia correspondiente se denomina equivalencia asintótica .${\displaystyle f:\mathbb {N} \to \mathbb {N} }$
• Las reducciones de tiempo polinomial , de muchos-uno (mapeo) y de Turing son preórdenes en clases de complejidad.
• Las relaciones de subtipificación suelen ser preórdenes. ^[2]
• Los pedidos anticipados de simulación son pedidos anticipados (de ahí el nombre).
• Relaciones de reducción en sistemas de reescritura abstracta .
• El preorden de abarcamiento en el conjunto de términos , definido por si un subtérmino de t es una instancia de sustitución de s .${\displaystyle s\lesssim t}$
• Subsunción theta , ^[3] que es cuando los literales en una fórmula disyuntiva de primer orden están contenidos por otro, después de aplicar una sustitución al anterior.

• Una categoría con como máximo un morfismo de cualquier objeto x a cualquier otro objeto y es un preorden. Tales categorías se denominan thin . Aquí los objetos corresponden a los elementos de y hay un morfismo para los objetos que están relacionados, cero en caso contrario. En este sentido, las categorías "generalizan" los preórdenes al permitir más de una relación entre objetos: cada morfismo es una relación de preorden distinta (con nombre).${\displaystyle P,}$
• Alternativamente, un conjunto preordenado puede entenderse como una categoría enriquecida , enriquecida sobre la categoría${\displaystyle 2=(0\to 1).}$

Más ejemplos:

• Todo espacio topológico finito da lugar a un preorden en sus puntos al definirse si y solo si x pertenece a cada entorno de y . Todo preorden finito puede formarse como el preorden de especialización de un espacio topológico de esta manera. Es decir, existe una correspondencia biunívoca entre topologías finitas y preórdenes finitos. Sin embargo, la relación entre espacios topológicos infinitos y sus preórdenes de especialización no es biunívoca.${\displaystyle x\lesssim y}$

• Una red es un preorden dirigido , es decir, cada par de elementos tiene un límite superior . La definición de convergencia a través de redes es importante en topología , donde los preórdenes no pueden reemplazarse por conjuntos parcialmente ordenados sin perder características importantes.

• La relación definida por si donde f es una función en algún preorden.${\displaystyle x\lesssim y}$${\displaystyle f(x)\lesssim f(y),}$
• Relación definida por si existe alguna inyección de x a y . La inyección puede reemplazarse por una sobreyección o cualquier tipo de función que preserve la estructura, como el homomorfismo de anillo o la permutación .${\displaystyle x\lesssim y}$
• La relación de incrustación para ordenamientos totales contables .

Ejemplo de un pedido anticipado total :

• Preferencia , según modelos comunes.

Toda relación binaria en un conjunto se puede extender a un preorden en tomando el cierre transitivo y el cierre reflexivo . El cierre transitivo indica conexión de caminos en si y solo si hay un camino de a${\displaystyle R}$${\displaystyle S}$${\displaystyle S}$${\displaystyle R^{+=}.}$${\displaystyle R:xR^{+}y}$${\displaystyle R}$${\displaystyle x}$${\displaystyle y.}$

Preorden residual izquierdo inducido por una relación binaria

Dada una relación binaria, la composición complementada forma un preorden llamado residuo izquierdo , ^[4] donde denota la relación inversa de y denota la relación complementaria de mientras que denota la composición de la relación .${\displaystyle R,}$${\displaystyle R\backslash R={\overline {R^{\textsf {T}}\circ {\overline {R}}}}}$${\displaystyle R^{\textsf {T}}}$${\displaystyle R,}$${\displaystyle {\overline {R}}}$${\displaystyle R,}$${\displaystyle \circ }$

Si un preorden también es antisimétrico , es decir, y implica entonces que es un orden parcial .${\displaystyle a\lesssim b}$${\displaystyle b\lesssim a}$${\displaystyle a=b,}$

Por otro lado, si es simétrica , es decir, si implica entonces es una relación de equivalencia .${\displaystyle a\lesssim b}$${\displaystyle b\lesssim a,}$

Un pedido anticipado es total si o para todos${\displaystyle a\lesssim b}$${\displaystyle b\lesssim a}$${\displaystyle a,b\in P.}$

Una clase preordenada es una clase equipada con un preorden. Cada conjunto es una clase y, por lo tanto, cada conjunto preordenado es una clase preordenada.

Los pedidos anticipados juegan un papel fundamental en varias situaciones:

• A cada preorden se le puede dar una topología, la topología de Alexandrov ; y, de hecho, cada preorden de un conjunto está en correspondencia biunívoca con una topología de Alexandrov de ese conjunto.
• Los preórdenes se pueden utilizar para definir álgebras interiores .
• Los pedidos anticipados proporcionan la semántica de Kripke para ciertos tipos de lógica modal .
• Los preórdenes se utilizan en la forzamiento en la teoría de conjuntos para demostrar resultados de consistencia e independencia . ^[5]

Téngase en cuenta que S ( n , k ) se refiere a números de Stirling del segundo tipo .

Como se explicó anteriormente, existe una correspondencia 1 a 1 entre preórdenes y pares (partición, orden parcial). Por lo tanto, el número de preórdenes es la suma del número de órdenes parciales en cada partición. Por ejemplo:

Para el intervalo es el conjunto de puntos x que satisfacen y también se escribe Contiene al menos los puntos a y b . Se puede optar por extender la definición a todos los pares Los intervalos adicionales están todos vacíos.${\displaystyle a\lesssim b,}$ ${\displaystyle [a,b]}$${\displaystyle a\lesssim x}$${\displaystyle x\lesssim b,}$${\displaystyle a\lesssim x\lesssim b.}$${\displaystyle (a,b)}$

Utilizando la relación estricta correspondiente " ", también se puede definir el intervalo como el conjunto de puntos x que satisfacen y también se escribe Un intervalo abierto puede estar vacío incluso si${\displaystyle <}$${\displaystyle (a,b)}$${\displaystyle a<x}$${\displaystyle x<b,}$${\displaystyle a<x<b.}$${\displaystyle a<b.}$

También se puede definir de manera similar .${\displaystyle [a,b)}$${\displaystyle (a,b]}$

• Orden parcial – preorden que es antisimétrico
• Relación de equivalencia : preorden que es simétrico
• Pedido anticipado total : pedido anticipado total
• Orden total : preorden que es antisimétrico y total
• Conjunto dirigido
• Categoría de sets preordenados
• Pedido previo al pozo
• Bien-cuasi-ordenamiento

• Schmidt, Gunther, "Matemáticas relacionales", Enciclopedia de matemáticas y sus aplicaciones, vol. 132, Cambridge University Press, 2011, ISBN 978-0-521-76268-7 
• Schröder, Bernd SW (2002), Conjuntos ordenados: una introducción , Boston: Birkhäuser, ISBN 0-8176-4128-9