Carga de color
Este artículo tiene varios problemas. Ayúdenos a mejorarlo o a discutir estos problemas en la página de discusión . ( Aprenda cómo y cuándo eliminar estos mensajes )
|
| Modelo estándar de física de partículas |
|---|
 |
La carga de color es una propiedad de los quarks y los gluones que está relacionada con las interacciones fuertes de las partículas en la teoría de la cromodinámica cuántica (QCD). Al igual que la carga eléctrica , determina cómo interactúan los quarks y los gluones a través de la fuerza fuerte; sin embargo, en lugar de haber solo cargas positivas y negativas, hay tres "cargas", comúnmente llamadas rojo, verde y azul. Además, hay tres "anticolores", comúnmente llamados anti-rojo, anti-verde y anti-azul. A diferencia de la carga eléctrica, la carga de color nunca se observa en la naturaleza: en todos los casos, rojo, verde y azul (o anti-rojo, anti-verde y anti-azul) o cualquier color y su anticolor se combinan para formar un sistema "neutral en cuanto al color". Por ejemplo, los tres quarks que componen cualquier barión tienen universalmente tres cargas de color diferentes, y los dos quarks que componen cualquier mesón tienen universalmente cargas de color opuestas.
La "carga de color" de los quarks y los gluones no tiene ninguna relación con el significado cotidiano de color , que se refiere a la frecuencia de los fotones , las partículas que median una fuerza fundamental diferente, el electromagnetismo . El término color y las etiquetas rojo, verde y azul se hicieron populares simplemente por la analogía vaga pero conveniente con los colores primarios .
Historia
Poco después de que Murray Gell-Mann y George Zweig propusieran la existencia de los quarks en 1964, la carga de color fue introducida implícitamente ese mismo año por Oscar W. Greenberg . [1] En 1965, Moo-Young Han y Yoichiro Nambu introdujeron explícitamente el color como una simetría de calibre. [1]
Han y Nambu designaron inicialmente este grado de libertad como el grupo SU(3) , pero en artículos posteriores se hizo referencia a él como "el modelo de tres tripletes". Una característica del modelo (que originalmente preferían Han y Nambu) era que permitía la presencia de quarks con carga integral, así como de quarks con carga fraccionaria propuestos inicialmente por Zweig y Gell-Mann.
Un poco más tarde, a principios de los años 1970, Gell-Mann, en varias conferencias, acuñó el nombre de color para describir el grado interno de libertad del modelo de tres tripletes y abogó por una nueva teoría de campo, denominada cromodinámica cuántica (QCD, por sus siglas en inglés) para describir la interacción de quarks y gluones dentro de los hadrones. En la QCD de Gell-Mann, cada quark y gluón tiene una carga eléctrica fraccionaria y lleva lo que se dio en llamar carga de color en el espacio del grado de libertad de color.
Rojo, verde y azul
En cromodinámica cuántica (QCD), el color de un quark puede tomar uno de tres valores o cargas: rojo, verde y azul. Un antiquark puede tomar uno de tres anticolores: llamados antirojo, antiverde y antiazul (representados como cian, magenta y amarillo, respectivamente). Los gluones son mezclas de dos colores, como el rojo y el antiverde, lo que constituye su carga de color. La QCD considera que ocho gluones de las nueve posibles combinaciones de color-anticolor son únicos; consulte ocho colores de gluones para obtener una explicación.
Los tres colores mezclados, los tres anticolores mezclados o una combinación de un color y su anticolor es "incolora" o "blanca" y tiene una carga neta de color de cero. Debido a una propiedad de la interacción fuerte llamada confinamiento de color , las partículas libres deben tener una carga de color de cero.
Un barión está compuesto de tres quarks, que deben ser de cada color: rojo, verde y azul; de la misma manera, un antibaryon está compuesto de tres antiquarks, uno de cada color: antirojo, antiverde y antiazul. Un mesón está formado por un quark y un antiquark; el quark puede ser de cualquier color y el antiquark tiene el anticolor correspondiente.
A continuación se ilustran las constantes de acoplamiento para partículas cargadas de color:
- Los colores de los quarks (rojo, verde, azul) se combinan para ser incoloros.
- Los anticolores de los quarks (antirojo, antiverde, antiazul) también se combinan para ser incoloros.
- Un hadrón con 3 quarks (rojo, verde, azul) antes de un cambio de color.
- El quark azul emite un gluón azul-antiverde
- El quark verde ha absorbido el gluón azul-antiverde y ahora es azul; el color permanece conservado
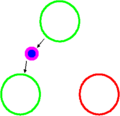
- Animación de la interacción dentro de un neutrón. Los gluones están representados como círculos con la carga de color en el centro y la carga anticolor en el exterior.
Líneas de campo de cargas de color
De manera análoga a un campo eléctrico y a las cargas eléctricas, la fuerza fuerte que actúa entre cargas de color se puede representar mediante líneas de campo. Sin embargo, las líneas de campo de color no se arquean tanto hacia afuera de una carga a otra, porque los gluones las atraen fuertemente (dentro de 1 fm ). [2] Este efecto confina a los quarks dentro de los hadrones .

Arriba : La carga de color tiene "estados neutros ternarios" así como neutralidad binaria (análoga a la carga eléctrica ).
Abajo : Combinaciones de quarks y antiquarks. [3] [4]
Constante de acoplamiento y carga
En una teoría cuántica de campos , una constante de acoplamiento y una carga son nociones diferentes pero relacionadas. La constante de acoplamiento establece la magnitud de la fuerza de interacción; por ejemplo, en electrodinámica cuántica , la constante de estructura fina es una constante de acoplamiento. La carga en una teoría de calibre tiene que ver con la forma en que una partícula se transforma bajo la simetría de calibre; es decir, su representación bajo el grupo de calibre. Por ejemplo, el electrón tiene carga −1 y el positrón tiene carga +1, lo que implica que la transformación de calibre tiene efectos opuestos sobre ellos en algún sentido. Específicamente, si se aplica una transformación de calibre local ϕ ( x ) en electrodinámica, entonces se encuentra (usando la notación de índice tensorial ): donde es el campo de fotones , y ψ es el campo de electrones con Q = −1 (una barra sobre ψ denota su antipartícula: el positrón). Dado que la QCD es una teoría no abeliana , las representaciones, y por lo tanto las cargas de color, son más complicadas. Se tratan en la siguiente sección.
Campos de quarks y gluones

En QCD el grupo de calibración es el grupo no abeliano SU(3) . El acoplamiento continuo se denota habitualmente por . Cada tipo de quark pertenece a la representación fundamental ( 3 ) y contiene un triplete de campos juntos denotados por . El campo de antiquark pertenece a la representación conjugada compleja ( 3 * ) y también contiene un triplete de campos. Podemos escribir
- y
El gluón contiene un octeto de campos (ver campo de gluones ), y pertenece a la representación adjunta ( 8 ), y puede escribirse utilizando las matrices de Gell-Mann como
(hay una suma implícita sobre a = 1, 2, ... 8). Todas las demás partículas pertenecen a la representación trivial ( 1 ) del color SU(3) . La carga de color de cada uno de estos campos está completamente especificada por las representaciones. Los quarks tienen una carga de color de rojo, verde o azul y los antiquarks tienen una carga de color de antirojo, antiverde o antiazul. Los gluones tienen una combinación de dos cargas de color (una de rojo, verde o azul y una de antirojo, antiverde o antiazul) en una superposición de estados que están dadas por las matrices de Gell-Mann. Todas las demás partículas tienen carga de color cero.
Los gluones correspondientes a y a veces se describen como de "carga cero" (como en la figura). Formalmente, estos estados se escriben como
- y
Si bien son "incoloros" en el sentido de que consisten en pares color-anticolor coincidentes, lo que los coloca en el centro de un diagrama de peso junto al estado singlete verdaderamente incoloro, aún participan en interacciones fuertes, en particular aquellas en las que los quarks interactúan sin cambiar de color.
Matemáticamente hablando, la carga de color de una partícula es el valor de un cierto operador de Casimir cuadrático en la representación de la partícula.
En el lenguaje simple presentado anteriormente, los tres índices "1", "2" y "3" en el triplete de quarks anterior se identifican generalmente con los tres colores. El lenguaje colorido pasa por alto el siguiente punto. Una transformación de calibre en color SU(3) se puede escribir como , donde es una matriz de 3 × 3 que pertenece al grupo SU(3). Por lo tanto, después de la transformación de calibre, los nuevos colores son combinaciones lineales de los colores antiguos. En resumen, el lenguaje simplificado presentado anteriormente no es invariante en cuanto a calibre.

La carga de color se conserva, pero la contabilidad que esto implica es más complicada que simplemente sumar las cargas, como se hace en la electrodinámica cuántica. Una forma sencilla de hacer esto es mirar el vértice de interacción en QCD y reemplazarlo por una representación de línea de color. El significado es el siguiente. Sea representa el i -ésimo componente de un campo de quarks (llamado vagamente el i- ésimo color). El color de un gluón se da de manera similar por , que corresponde a la matriz de Gell-Mann particular con la que está asociado. Esta matriz tiene índices i y j . Estas son las etiquetas de color en el gluón. En el vértice de interacción uno tiene q i → g ij + q j . La representación de línea de color rastrea estos índices. La conservación de la carga de color significa que los extremos de estas líneas de color deben estar en el estado inicial o final, equivalentemente, que ninguna línea se rompa en el medio de un diagrama.

Como los gluones tienen carga de color, dos gluones también pueden interactuar. Un vértice de interacción típico (llamado vértice de tres gluones) para los gluones implica g + g → g. Esto se muestra aquí, junto con su representación en líneas de color. Los diagramas de líneas de color se pueden reformular en términos de leyes de conservación del color; sin embargo, como se señaló anteriormente, este no es un lenguaje invariante de calibre. Nótese que en una teoría de calibre no abeliana típica, el bosón de calibre lleva la carga de la teoría y, por lo tanto, tiene interacciones de este tipo; por ejemplo, el bosón W en la teoría electrodébil. En la teoría electrodébil, el W también lleva carga eléctrica y, por lo tanto, interactúa con un fotón.
Véase también
Referencias
- ^ ab Greenberg, Oscar Wallace (2009), Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (eds.), "Grado de libertad de la carga de color en la física de partículas", Compendio de física cuántica , Berlín, Heidelberg: Springer, págs. 109-111, doi :10.1007/978-3-540-70626-7_32, ISBN 978-3-540-70626-7, consultado el 17 de septiembre de 2024
- ^ R. Resnick, R. Eisberg (1985), Física cuántica de átomos, moléculas, sólidos, núcleos y partículas (2.ª ed.), John Wiley & Sons, pág. 684, ISBN 978-0-471-87373-0
- ^ Parker, CB (1994), Enciclopedia McGraw Hill de Física (2.ª ed.), Mc Graw Hill, ISBN 978-0-07-051400-3
- ^ M. Mansfield, C. O'Sullivan (2011), Comprensión de la física (4.ª ed.), John Wiley & Sons, ISBN 978-0-47-0746370
Lectura adicional
- Georgi, Howard (1999), Álgebras de Lie en física de partículas , Perseus Books Group, ISBN 978-0-7382-0233-4.
- Griffiths, David J. (1987), Introducción a las partículas elementales , Nueva York: John Wiley & Sons, ISBN 978-0-471-60386-3.
- Christman, J. Richard (2001), "Color y encanto" (PDF) , documento PHYSNET MISN-0-283.
- Hawking, Stephen (1998), Una breve historia del tiempo , Bantam Dell Publishing Group, ISBN 978-0-553-10953-5.
- Close, Frank (2007), La nueva cebolla cósmica , Taylor & Francis, ISBN 978-1-58488-798-0.







![{\displaystyle {\begin{aligned}A_{\mu }&\to A_{\mu }+\partial _{\mu }\,\phi (x)\\\psi &\to \exp \left[+i\,Q\phi (x)\right]\;\psi \\{\bar {\psi }}&\to \exp \left[-i\,Q\phi (x)\right]\;{\bar {\psi }}~,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e95dbc8e4de7e10d356729b998cb570c3cda4f54)














