CIELUV

En colorimetría , el espacio de color CIE 1976 L *, u *, v * , conocido comúnmente por su abreviatura CIELUV , es un espacio de color adoptado por la Comisión Internacional de Iluminación (CIE) en 1976, como una transformación fácil de calcular del espacio de color CIE XYZ de 1931 , pero que intentaba lograr uniformidad perceptual . Se utiliza ampliamente para aplicaciones como gráficos de computadora que tratan con luces de colores. Aunque las mezclas aditivas de luces de diferentes colores caerán en una línea en el diagrama de cromaticidad uniforme de CIELUV (llamado CIE 1976 UCS ), dichas mezclas aditivas no caerán, contrariamente a la creencia popular, a lo largo de una línea en el espacio de color CIELUV a menos que las mezclas sean constantes en luminosidad .

CIELUV es un espacio de color de valencia cromática de Adams y es una actualización del espacio de color CIE 1964 ( U *, V *, W *) (CIEUVW). Las diferencias incluyen una escala de luminosidad ligeramente modificada y una escala de cromaticidad uniforme modificada, en la que una de las coordenadas, v ′, es 1,5 veces más grande que v en su predecesor de 1960. CIELUV y CIELAB fueron adoptados simultáneamente por la CIE cuando no se pudo formar un consenso claro detrás de solo uno u otro de estos dos espacios de color.

CIELUV utiliza una adaptación de punto blanco de tipo Judd (traslacional) (en contraste con CIELAB, que utiliza una transformada de von Kries ). ^[1] Esto puede producir resultados útiles cuando se trabaja con un solo iluminante, pero puede predecir colores imaginarios (es decir, fuera del locus espectral ) cuando se intenta usarlo como una transformada de adaptación cromática . ^[2] También se ha demostrado que la transformada de adaptación traslacional utilizada en CIELUV tiene un rendimiento deficiente en la predicción de colores correspondientes. ^[3]

Por definición, 0 ≤ L * ≤ 100 .

CIELUV se basa en CIEUVW y es otro intento de definir una codificación con uniformidad en la perceptibilidad de las diferencias de color . ^[4] Las relaciones no lineales para L *, u * y v * se dan a continuación: ^[4]

${\displaystyle {\begin{aligned}L^{*}&={\begin{cases}\left({\frac {29}{3}}\right)^{3}Y/Y_{n},&Y/Y_{n}\leq \left({\frac {6}{29}}\right)^{3}\\116\left(Y/Y_{n}\right)^{1/3}-16,&Y/Y_{n}>\left({\frac {6}{29}}\right)^{3}\end{cases}}\\u^{*}&=13L^{*}\cdot (u^{\prime }-u_{n}^{\prime })\\v^{*}&=13L^{*}\cdot (v^{\prime }-v_{n}^{\prime })\end{aligned}}}$

Las cantidades u ′ _n y v ′ _n son las coordenadas de cromaticidad ( u ′ , v ′ ) de un "objeto blanco especificado" – que puede denominarse punto blanco – e Y _n es su luminancia. En el modo de reflexión, esto se toma a menudo (pero no siempre) como el ( u ′ , v ′ ) del difusor reflector perfecto bajo ese iluminante. (Por ejemplo, para el observador de 2° y el iluminante estándar C, u ′ _n = 0,2009 , v ′ _n = 0,4610 .) Las ecuaciones para u ′ y v ′ se dan a continuación: ^{[5] [6]}

${\displaystyle {\begin{aligned}u^{\prime }&={\frac {4X}{X+15Y+3Z}}&={\frac {4x}{-2x+12y+3}}\\v^{\prime }&={\frac {9Y}{X+15Y+3Z}}&={\frac {9y}{-2x+12y+3}}\end{aligned}}}$

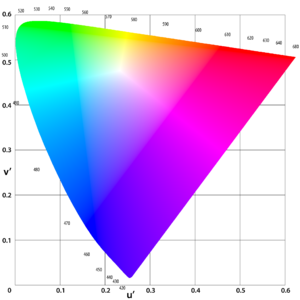
La transformación de ( u ′, v ′) a ( x , y ) es: ^[6]

${\displaystyle {\begin{aligned}x&={\frac {9u^{\prime }}{6u^{\prime }-16v^{\prime }+12}}\\y&={\frac {4v^{\prime }}{6u^{\prime }-16v^{\prime }+12}}\end{aligned}}}$

La transformación de CIELUV a XYZ se realiza de la siguiente manera: ^[6]

${\displaystyle {\begin{aligned}u^{\prime }&={\frac {u^{*}}{13L^{*}}}+u_{n}^{\prime }\\v^{\prime }&={\frac {v^{*}}{13L^{*}}}+v_{n}^{\prime }\\Y&={\begin{cases}Y_{n}\cdot L^{*}\cdot \left({\frac {3}{29}}\right)^{3},&L^{*}\leq 8\\Y_{n}\cdot \left({\frac {L^{*}+16}{116}}\right)^{3},&L^{*}>8\end{cases}}\\X&=Y\cdot {\frac {9u^{\prime }}{4v^{\prime }}}\\Z&=Y\cdot {\frac {12-3u^{\prime }-20v^{\prime }}{4v^{\prime }}}\\\end{aligned}}}$

El espacio de color CIELCh _uv o HCL (tono-croma-luminancia) se considera cada vez más en la comunidad de visualización de información como una forma de ayudar a presentar datos sin el sesgo implícito en el uso de saturación variable . ^{[7] [8] [9]}

La versión cilíndrica de CIELUV se conoce como CIELCh _uv , o CIELChuv, CIELCh(uv) o CIEHLC _uv , donde C * _uv es el croma y h _uv es el tono : ^[6]

${\displaystyle C_{uv}^{*}=\operatorname {hypot} (u^{*},v^{*})={\sqrt {(u^{*})^{2}+(v^{*})^{2}}},}$

${\displaystyle h_{uv}=\operatorname {atan2} (v^{*},u^{*}),}$

donde la función atan2 , una "arcotangente de dos argumentos", calcula el ángulo polar a partir de un par de coordenadas cartesianas.

Además, el correlato de saturación se puede definir como

${\displaystyle s_{uv}={\frac {C^{*}}{L^{*}}}=13{\sqrt {(u'-u'_{n})^{2}+(v'-v'_{n})^{2}}}.}$

Existen correlaciones similares de croma y tono, pero no de saturación, para CIELAB. Consulte Coloración para obtener más información sobre la saturación.

La diferencia de color se puede calcular utilizando la distancia euclidiana de las coordenadas ( L *, u *, v *) . ^[6] De ello se deduce que una distancia de cromaticidad de corresponde al mismo Δ E * _uv que una diferencia de luminosidad de Δ L * = 1 , en analogía directa con CIEUVW.${\displaystyle {\sqrt {(\Delta u')^{2}+(\Delta v')^{2}}}=1/13}$

La métrica euclidiana también se puede utilizar en CIELCh, con ese componente de Δ E * _uv atribuible a la diferencia de tono como ^[4] Δ H * = √ C * ₁ C * ₂ 2 sin (Δ h /2) , donde Δ h = h ₂ − h ₁ .

• YUV
• Espacio de color CIELAB

• Diagramas de cromaticidad, incluidos los CIE 1931, CIE 1960, CIE 1976
• Caja de herramientas MATLAB Colorlab para el cálculo de la ciencia del color y la reproducción precisa del color (por Jesús Malo y María José Luque, Universitat de Valencia). Incluye colorimetría triestímulo estándar CIE y transformaciones a una serie de modelos de apariencia de color no lineales (CIELAB, CIE CAM, etc.).