Ciclo de Born-Haber
Enfoque para el análisis de las energías de reacción

El ciclo de Born-Haber es un método para analizar las energías de reacción . Debe su nombre a dos científicos alemanes , Max Born y Fritz Haber , quienes lo desarrollaron en 1919. [1] [2] [3] También fue formulado de forma independiente por Kasimir Fajans [4] y publicado simultáneamente en la misma revista. [1] El ciclo se ocupa de la formación de un compuesto iónico a partir de la reacción de un metal (a menudo un elemento del Grupo I o del Grupo II ) con un halógeno u otro elemento no metálico como el oxígeno .

Los ciclos de Born-Haber se utilizan principalmente como un medio para calcular la energía reticular (o más precisamente, la entalpía [nota 1] ), que no se puede medir directamente de otra manera. La entalpía reticular es el cambio de entalpía involucrado en la formación de un compuesto iónico a partir de iones gaseosos (un proceso exotérmico ), o a veces se define como la energía para romper el compuesto iónico en iones gaseosos (un proceso endotérmico ). Un ciclo de Born-Haber aplica la ley de Hess para calcular la entalpía reticular comparando el cambio de entalpía estándar de formación del compuesto iónico (a partir de los elementos) con la entalpía requerida para formar iones gaseosos a partir de los elementos .

Este cálculo de red es complejo. Para formar iones gaseosos a partir de elementos es necesario atomizar los elementos (convertir cada uno en átomos gaseosos) y luego ionizar los átomos. Si el elemento es normalmente una molécula, primero tenemos que considerar su entalpía de disociación de enlace (ver también energía de enlace ). La energía requerida para eliminar uno o más electrones para formar un catión es una suma de energías de ionización sucesivas ; por ejemplo, la energía necesaria para formar Mg 2+ es la energía de ionización requerida para eliminar el primer electrón de Mg, más la energía de ionización requerida para eliminar el segundo electrón de Mg + . La afinidad electrónica se define como la cantidad de energía liberada cuando se agrega un electrón a un átomo o molécula neutros en estado gaseoso para formar un ion negativo.

El ciclo de Born-Haber se aplica únicamente a sólidos completamente iónicos, como ciertos haluros alcalinos . La mayoría de los compuestos incluyen contribuciones covalentes e iónicas a la unión química y a la energía reticular, que se representa mediante un ciclo termodinámico de Born-Haber extendido. [5] El ciclo de Born-Haber extendido se puede utilizar para estimar la polaridad y las cargas atómicas de compuestos polares.

Ejemplos

Formación de LiF

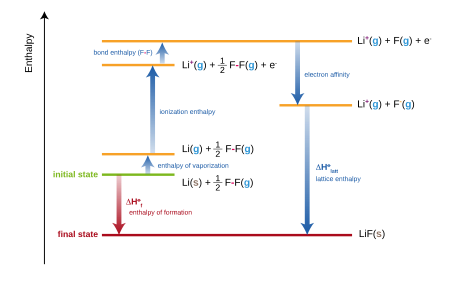
Ciclo de Born-Haber para el cambio de entalpía estándar de formación de fluoruro de litio . ΔH latt corresponde a U L en el texto. La flecha hacia abajo "afinidad electrónica" muestra la cantidad negativa –EA F , ya que EA F se define generalmente como positiva.

La entalpía de formación del fluoruro de litio (LiF) a partir de sus elementos en sus estados estándar (Li(s) y F 2 (g)) se modela en cinco pasos en el diagrama:

  1. Entalpía de atomización del litio
  2. Entalpía de ionización del litio
  3. Entalpía de atomización del flúor
  4. Afinidad electrónica del flúor
  5. Entalpía reticular

La suma de las energías de cada paso del proceso debe ser igual a la entalpía de formación del fluoruro de litio . Δ yo F {\displaystyle \Delta H_{f}}

Δ yo F = V + 1 2 B + I mi METRO − EA incógnita + tú yo {\displaystyle \Delta H_{f}=V+{\frac {1}{2}}B+{\mathit {IE}}_{{\ce {M}}}-{\ce {EA}}_{{ \ce {X}}}+U_ {L}}
  • V es la entalpía de sublimación de los átomos de metal (litio)
  • B es la entalpía de enlace (de F 2 ). Se utiliza el coeficiente 1/2 porque la reacción de formación es Li + 1/2 F 2 → LiF.
  • ES DECIR METRO {\displaystyle {\ce {{\mathit {IE}}_{M}}}} es la energía de ionización del átomo de metal: METRO + ES DECIR METRO ⟶ METRO + + mi − {\displaystyle {\ce {{M}+{\mathit {IE}}_{M}->{M+}+e^{-}}}}
  • EA incógnita {\displaystyle {\ce {{\mathit {EA}}_{X}}}} es la afinidad electrónica del átomo no metálico X (flúor)
  • tú yo Estilo de visualización U_{L} es la entalpía reticular (definida aquí como exotérmica)

La entalpía neta de formación y las primeras cuatro de las cinco energías se pueden determinar experimentalmente, pero la entalpía reticular no se puede medir directamente. En cambio, la entalpía reticular se calcula restando las otras cuatro energías del ciclo de Born-Haber de la entalpía neta de formación. Se aplica un cálculo similar para cualquier metal que no sea litio y/o cualquier no metal que no sea flúor. [6]

La palabra ciclo se refiere al hecho de que también se puede igualar a cero el cambio de entalpía total para un proceso cíclico, que comienza y termina con LiF(s) en el ejemplo. Esto lleva a

0 = − Δ yo F + V + 1 2 B + I mi METRO − mi A incógnita + tú yo {\displaystyle 0=-\Delta H_{f}+V+{\frac {1}{2}}B+{\mathit {IE}}_{{\ce {M}}}-{\mathit {EA}}_{{\ce {X}}}+U_{L}}

lo que es equivalente a la ecuación anterior.

Formación de NaBr

A temperaturas ordinarias, Na es sólido y Br 2 es líquido, por lo que la entalpía de vaporización del bromo líquido se añade a la ecuación:

Δ yo F = V + 1 2 B + 1 2 Δ en a pag yo + I mi METRO − EA incógnita + tú yo {\displaystyle \Delta H_{f}=V+{\frac {1}{2}}B+{\frac {1}{2}}\Delta _{vap}H+{\mathit {IE}}_{{\ ce {M}}}-{\ce {EA}}_{{\ce {X}}}+U_{L}}

En la ecuación anterior, es la entalpía de vaporización de Br 2 a la temperatura de interés (generalmente en kJ/mol). Δ en a pag yo {\displaystyle \Delta _{vap}H}

Véase también

Notas

  1. ^ La diferencia entre energía y entalpía es muy pequeña y a menudo ambos términos se intercambian libremente.

Referencias

  1. ^ ab Morris, DFC; Short, EL (6 de diciembre de 1969). "La correlación de Born-Fajans-Haber". Nature . 224 (5223): 950–952. Bibcode :1969Natur.224..950M. doi :10.1038/224950a0. S2CID  4199898. Un nombre más correcto sería correlación termoquímica de Born–Fajans–Haber.
  2. ^ M. Born Verhandlungen der Deutschen Physikalischen Gesellschaft 1919, 21 , 679–685.
  3. ^ F. Haber Verhandlungen der Deutschen Physikalischen Gesellschaft 1919, 21 , 750–768.
  4. ^ K. Fajans Verhandlungen der Deutschen Physikalischen Gesellschaft 1919, 21 , 714–722.
  5. ^ H. Heinz y UW Suter Revista de química física B 2004, 108 , 18341–18352.
  6. ^ Moore, Stanitski y Jurs. Química: la ciencia molecular. 3.ª ed. 2008. ISBN 0-495-10521-X . págs. 320–321. 
  • ChemGuy sobre el ciclo de Born-Haber
Obtenido de "https://es.wikipedia.org/w/index.php?title=Ciclo_de_Born-Haber&oldid=1190438676"