Chirrido
Señal de barrido de frecuencia
Una forma de onda de chirrido lineal; una onda sinusoidal que aumenta su frecuencia linealmente con el tiempo

Un chirp es una señal en la que la frecuencia aumenta ( up-chirp ) o disminuye ( down-chirp ) con el tiempo. En algunas fuentes, el término chirp se usa indistintamente con señal de barrido . [1] Se aplica comúnmente a sistemas de sonar , radar y láser , y a otras aplicaciones, como en comunicaciones de espectro ensanchado (ver chirp de espectro ensanchado ). Este tipo de señal está inspirado biológicamente y ocurre como un fenómeno debido a la dispersión (una dependencia no lineal entre la frecuencia y la velocidad de propagación de los componentes de la onda). Por lo general, se compensa mediante el uso de un filtro adaptado, que puede ser parte del canal de propagación. Sin embargo, dependiendo de la medida de rendimiento específica, existen mejores técnicas tanto para el radar como para la comunicación. Dado que se utilizó en el radar y el espacio, también se ha adoptado para los estándares de comunicación. Para aplicaciones de radar automotriz, generalmente se llama forma de onda modulada en frecuencia lineal (LFMW). [2]

En el uso de espectro ensanchado, los dispositivos de ondas acústicas de superficie (SAW) se utilizan a menudo para generar y demodular las señales chirriantes. En óptica , los pulsos láser ultracortos también presentan chirridos, que, en los sistemas de transmisión óptica, interactúan con las propiedades de dispersión de los materiales, aumentando o disminuyendo la dispersión total del pulso a medida que se propaga la señal. El nombre es una referencia al sonido chirriante que emiten los pájaros; consulte vocalización de los pájaros .

Definiciones

Las definiciones básicas que se encuentran aquí se traducen como las magnitudes físicas comunes: ubicación (fase), velocidad (velocidad angular) y aceleración (vibración). Si una forma de onda se define como: incógnita ( a ) = pecado ⁡ ( ϕ ( a ) ) {\displaystyle x(t)=\sin \left(\phi (t)\right)}

entonces la frecuencia angular instantánea , ω , se define como la tasa de fase dada por la primera derivada de la fase, siendo la frecuencia ordinaria instantánea, f , su versión normalizada: ω ( a ) = d ϕ ( a ) d a , F ( a ) = ω ( a ) 2 π {\displaystyle \omega (t)={\frac {d\phi (t)}{dt}},\,f(t)={\frac {\omega (t)}{2\pi }}}

Finalmente, la vibración angular instantánea (símbolo γ ) se define como la segunda derivada de la fase instantánea o la primera derivada de la frecuencia angular instantánea. La vibración angular tiene unidades de radianes por segundo cuadrado (rad/s 2 ); por lo tanto, es análoga a la aceleración angular . γ ( t ) = d 2 ϕ ( t ) d t 2 = d ω ( t ) d t {\displaystyle \gamma (t)={\frac {d^{2}\phi (t)}{dt^{2}}}={\frac {d\omega (t)}{dt}}}

La chirridez ordinaria instantánea (símbolo c ) es una versión normalizada, definida como la tasa de cambio de la frecuencia instantánea: [3] La chirridez ordinaria tiene unidades de segundos recíprocos cuadrados (s −2 ); por lo tanto, es análoga a la aceleración rotacional . c ( t ) = γ ( t ) 2 π = d f ( t ) d t {\displaystyle c(t)={\frac {\gamma (t)}{2\pi }}={\frac {df(t)}{dt}}}

Tipos

Lineal

Espectrograma de un chirrido lineal. El gráfico del espectrograma muestra la tasa lineal de cambio de frecuencia en función del tiempo, en este caso de 0 a 7 kHz, repitiéndose cada 2,3 segundos. La intensidad del gráfico es proporcional al contenido de energía en la señal en la frecuencia y el tiempo indicados.
Chirrido lineal
Ejemplo de sonido de chirrido lineal (cinco repeticiones)
¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

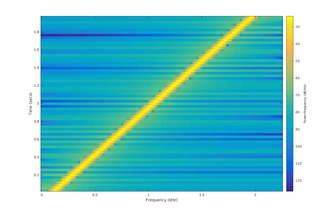
En un chirrido de frecuencia lineal o simplemente chirrido lineal , la frecuencia instantánea varía exactamente de forma lineal con el tiempo: donde es la frecuencia inicial (en el tiempo ) y es la tasa de chirrido, que se supone constante: f ( t ) {\displaystyle f(t)} f ( t ) = c t + f 0 , {\displaystyle f(t)=ct+f_{0},} f 0 {\displaystyle f_{0}} t = 0 {\displaystyle t=0} c {\displaystyle c} c = f 1 − f 0 T = Δ f Δ t . {\displaystyle c={\frac {f_{1}-f_{0}}{T}}={\frac {\Delta f}{\Delta t}}.}

Aquí está la frecuencia final y el tiempo que tarda en barrer de a . f 1 {\displaystyle f_{1}} T {\displaystyle T} f 0 {\displaystyle f_{0}} f 1 {\displaystyle f_{1}}

La función de dominio de tiempo correspondiente para la fase de cualquier señal oscilante es la integral de la función de frecuencia, ya que se espera que la fase crezca como , es decir, que la derivada de la fase sea la frecuencia angular . ϕ ( t + Δ t ) ≃ ϕ ( t ) + 2 π f ( t ) Δ t {\displaystyle \phi (t+\Delta t)\simeq \phi (t)+2\pi f(t)\,\Delta t} ϕ ′ ( t ) = 2 π f ( t ) {\displaystyle \phi '(t)=2\pi \,f(t)}

Para el chirrido lineal, esto da como resultado: ϕ ( t ) = ϕ 0 + 2 π ∫ 0 t f ( τ ) d τ = ϕ 0 + 2 π ∫ 0 t ( c τ + f 0 ) d τ = ϕ 0 + 2 π ( c 2 t 2 + f 0 t ) , {\displaystyle {\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi \int _{0}^{t}\left(c\tau +f_{0}\right)\,d\tau \\&=\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right),\end{aligned}}}

donde es la fase inicial (en el momento ). Por lo tanto, también se denomina señal de fase cuadrática . [4] ϕ 0 {\displaystyle \phi _{0}} t = 0 {\displaystyle t=0}

La función de dominio temporal correspondiente para un chirrido lineal sinusoidal es el seno de la fase en radianes: x ( t ) = sin ⁡ [ ϕ 0 + 2 π ( c 2 t 2 + f 0 t ) ] {\displaystyle x(t)=\sin \left[\phi _{0}+2\pi \left({\frac {c}{2}}t^{2}+f_{0}t\right)\right]}

Exponencial

Una forma de onda de chirrido exponencial; una onda sinusoidal que aumenta su frecuencia exponencialmente con el tiempo
Espectrograma de un chirrido exponencial. La tasa exponencial de cambio de frecuencia se muestra como una función del tiempo, en este caso desde casi 0 hasta 8 kHz repitiéndose cada segundo. También se puede ver en este espectrograma una caída de frecuencia a 6 kHz después del pico, probablemente un artefacto del método específico empleado para generar la forma de onda.
Chirrido exponencial
Ejemplo de sonido de chirrido exponencial (cinco repeticiones)
¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

En un chirrido geométrico , también llamado chirrido exponencial , la frecuencia de la señal varía con una relación geométrica a lo largo del tiempo. En otras palabras, si se eligen dos puntos en la forma de onda, y , y el intervalo de tiempo entre ellos se mantiene constante, la relación de frecuencias también será constante. [5] [6] t 1 {\displaystyle t_{1}} t 2 {\displaystyle t_{2}} T = t 2 − t 1 {\displaystyle T=t_{2}-t_{1}} f ( t 2 ) / f ( t 1 ) {\displaystyle f\left(t_{2}\right)/f\left(t_{1}\right)}

En un chirrido exponencial, la frecuencia de la señal varía exponencialmente en función del tiempo: donde es la frecuencia inicial (en ), y es la tasa de cambio exponencial en la frecuencia. f ( t ) = f 0 k t T {\displaystyle f(t)=f_{0}k^{\frac {t}{T}}} f 0 {\displaystyle f_{0}} t = 0 {\displaystyle t=0} k {\displaystyle k}

k = f 1 f 0 {\displaystyle k={\frac {f_{1}}{f_{0}}}}

¿Dónde está la frecuencia final del chirrido (en )? f 1 {\displaystyle f_{1}} t = T {\displaystyle t=T}

A diferencia del chirrido lineal, que tiene un chirrido constante, un chirrido exponencial tiene una tasa de frecuencia que aumenta exponencialmente.

La función de dominio de tiempo correspondiente para la fase de un chirrido exponencial es la integral de la frecuencia: donde es la fase inicial (en ). ϕ ( t ) = ϕ 0 + 2 π ∫ 0 t f ( τ ) d τ = ϕ 0 + 2 π f 0 ∫ 0 t k τ T d τ = ϕ 0 + 2 π f 0 ( T k t T ln ⁡ ( k ) ) {\displaystyle {\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi f_{0}\int _{0}^{t}k^{\frac {\tau }{T}}d\tau \\&=\phi _{0}+2\pi f_{0}\left({\frac {Tk^{\frac {t}{T}}}{\ln(k)}}\right)\end{aligned}}} ϕ 0 {\displaystyle \phi _{0}} t = 0 {\displaystyle t=0}

La función de dominio temporal correspondiente para un chirrido exponencial sinusoidal es el seno de la fase en radianes: x ( t ) = sin ⁡ [ ϕ 0 + 2 π f 0 ( T k t T ln ⁡ ( k ) ) ] {\displaystyle x(t)=\sin \left[\phi _{0}+2\pi f_{0}\left({\frac {Tk^{\frac {t}{T}}}{\ln(k)}}\right)\right]}

Al igual que en el caso del Chirp lineal, la frecuencia instantánea del Chirp exponencial consiste en la frecuencia fundamental acompañada de armónicos adicionales . [ cita requerida ] f ( t ) = f 0 k t T {\displaystyle f(t)=f_{0}k^{\frac {t}{T}}}

Hiperbólico

Los chirridos hiperbólicos se utilizan en aplicaciones de radar, ya que muestran la máxima respuesta del filtro adaptado después de ser distorsionados por el efecto Doppler. [7]

En un chirrido hiperbólico, la frecuencia de la señal varía hiperbólicamente en función del tiempo: f ( t ) = f 0 f 1 T ( f 0 − f 1 ) t + f 1 T {\displaystyle f(t)={\frac {f_{0}f_{1}T}{(f_{0}-f_{1})t+f_{1}T}}}

La función de dominio de tiempo correspondiente para la fase de un chirrido hiperbólico es la integral de la frecuencia: donde es la fase inicial (en ). ϕ ( t ) = ϕ 0 + 2 π ∫ 0 t f ( τ ) d τ = ϕ 0 + 2 π − f 0 f 1 T f 1 − f 0 ln ⁡ ( 1 − f 1 − f 0 f 1 T t ) {\displaystyle {\begin{aligned}\phi (t)&=\phi _{0}+2\pi \int _{0}^{t}f(\tau )\,d\tau \\&=\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}T}}t\right)\end{aligned}}} ϕ 0 {\displaystyle \phi _{0}} t = 0 {\displaystyle t=0}

La función de dominio temporal correspondiente para un chirrido hiperbólico sinusoidal es el seno de la fase en radianes: x ( t ) = sin ⁡ [ ϕ 0 + 2 π − f 0 f 1 T f 1 − f 0 ln ⁡ ( 1 − f 1 − f 0 f 1 T t ) ] {\displaystyle x(t)=\sin \left[\phi _{0}+2\pi {\frac {-f_{0}f_{1}T}{f_{1}-f_{0}}}\ln \left(1-{\frac {f_{1}-f_{0}}{f_{1}T}}t\right)\right]}

Generación

Una señal de chirrido se puede generar con circuitos analógicos a través de un oscilador controlado por voltaje (VCO) y un voltaje de control de rampa lineal o exponencial . [8] También se puede generar digitalmente mediante un procesador de señal digital (DSP) y un convertidor digital a analógico (DAC), utilizando un sintetizador digital directo (DDS) y variando el paso en el oscilador controlado numéricamente. [9] También se puede generar mediante un oscilador YIG . [ aclaración necesaria ]

Relación con una señal de impulso

Señales de chirrido e impulso y sus componentes espectrales (seleccionados) . En la parte inferior se muestran cuatro componentes monocromáticos , ondas sinusoidales de diferente frecuencia. La línea roja en las ondas indica el cambio de fase relativo a las otras ondas sinusoidales, originadas a partir de la característica de chirrido. La animación elimina el cambio de fase paso a paso (como con el filtrado adaptado ), lo que da como resultado un pulso sinc cuando no queda ningún cambio de fase relativo.

Una señal chirp comparte el mismo contenido espectral con una señal de impulso . Sin embargo, a diferencia de la señal de impulso, los componentes espectrales de la señal chirp tienen diferentes fases, [10] [11] [12] [13] es decir, sus espectros de potencia son similares pero los espectros de fase son distintos. La dispersión de un medio de propagación de señales puede dar como resultado una conversión no intencional de señales de impulso en chirps ( Whistler ). Por otro lado, muchas aplicaciones prácticas, como los amplificadores de pulsos chirp o los sistemas de ecolocalización, [12] utilizan señales chirp en lugar de impulsos debido a su relación de potencia pico a promedio (PAPR) inherentemente más baja . [13]

Usos y ocurrencias

Modulación de chirrido

La modulación de chirrido, o modulación de frecuencia lineal para comunicación digital, fue patentada por Sidney Darlington en 1954 y Winkler realizó trabajos posteriores importantes en 1962. Este tipo de modulación emplea formas de onda sinusoidales cuya frecuencia instantánea aumenta o disminuye linealmente con el tiempo. Estas formas de onda se conocen comúnmente como chirridos lineales o simplemente chirridos.

Por lo tanto, la velocidad a la que cambia su frecuencia se denomina frecuencia de chirrido . En la modulación binaria de chirrido, los datos binarios se transmiten asignando los bits a chirridos de frecuencias de chirrido opuestas. Por ejemplo, durante un período de bit, a "1" se le asigna un chirrido con una frecuencia positiva a y a "0" un chirrido con una frecuencia negativa − a . Los chirridos se han utilizado ampliamente en aplicaciones de radar y, como resultado, se dispone de fuentes avanzadas para la transmisión y filtros adaptados para la recepción de chirridos lineales.

(a) En el procesamiento de imágenes, rara vez se produce una periodicidad directa, sino que, más bien, se encuentra una periodicidad en perspectiva. (b) Las estructuras repetidas, como el espacio oscuro alternado dentro de las ventanas y el espacio de luz del hormigón blanco, "chirrían" (aumentan en frecuencia) hacia la derecha. (c) Por lo tanto, el chirrido que mejor se ajusta al procesamiento de imágenes es a menudo un chirrido proyectivo.

Transformación de Chirplet

Otro tipo de chirrido es el chirrido proyectivo, de la forma: que tiene los tres parámetros a (escala), b (traslación) y c (chirrido). El chirrido proyectivo es ideal para el procesamiento de imágenes y forma la base para la transformada de chirplet proyectivo . [3] g = f [ a ⋅ x + b c ⋅ x + 1 ] , {\displaystyle g=f\left[{\frac {a\cdot x+b}{c\cdot x+1}}\right],}

Sonido de la tecla

Un cambio en la frecuencia del código Morse con respecto a la frecuencia deseada, debido a una mala estabilidad en el oscilador de RF , se conoce como chirrido , [14] y en el sistema RST se le asigna una letra "C" añadida.

Véase también

Referencias

  1. ^ Weisstein, Eric W. "Sweep Signal". De MathWorld, un recurso web de Wolfram. http://mathworld.wolfram.com/SweepSignal.html
  2. ^ Lee, Tae-Yun; Jeon, Se-Yeon; Han, Junghwan; Skvortsov, Vladimir; Nikitin, Konstantin; Ka, Min-Ho (2016). "Una técnica simplificada para mediciones de distancia y velocidad de múltiples objetos en movimiento utilizando una señal modulada en frecuencia lineal". IEEE Sensors Journal . 16 (15): 5912–5920. Código Bibliográfico :2016ISenJ..16.5912L. doi :10.1109/JSEN.2016.2563458. S2CID  41233620.
  3. ^ ab Mann, Steve y Haykin, Simon; La transformación Chirplet: una generalización de la transformación Logon de Gabor; Vision Interface '91.[1]
  4. ^ Easton, RL (2010). Métodos de Fourier en imágenes. Wiley. pág. 703. ISBN 9781119991861. Recuperado el 3 de diciembre de 2014 .
  5. ^ Li, X. (15 de noviembre de 2022), Métodos de análisis de tiempo y frecuencia en señales GW , consultado el 10 de febrero de 2023
  6. ^ Mamou, J.; Ketterling, JA; Silverman, RH (2008). "Chirrido lineal". NCBI . 55 (2): 508–513. doi :10.1109/TUFFC.2008.670. PMC 2652352 . PMID  18334358. 
  7. ^ Yang, J.; Sarkar, TK (2006). "Propiedad invariante Doppler de formas de onda moduladas en frecuencia hiperbólica". Microwave and Optical Technology Letters . 48 (6): 1174–1179. doi :10.1002/mop.21573. S2CID  16476642.
  8. ^ "Señal de chirrido: descripción general | Temas de ScienceDirect" www.sciencedirect.com . Consultado el 10 de febrero de 2023 .
  9. ^ Yang, Heein; Ryu, Sang-Burm; Lee, Hyun-Chul; Lee, Sang-Gyu; Yong, Sang-Soon; Kim, Jae-Hyun (2014). "Implementación de un generador de señales DDS chirp en FPGA". Conferencia internacional sobre convergencia de tecnologías de la información y la comunicación (ICTC) de 2014. págs. 956–959. doi :10.1109/ICTC.2014.6983343. ISBN 978-1-4799-6786-5.S2CID206870096  .​
  10. ^ "Pulsos chirriantes". setiathome.berkeley.edu . Consultado el 3 de diciembre de 2014 .
  11. ^ Easton, RL (2010). Métodos de Fourier en imágenes. Wiley. pág. 700. ISBN 9781119991861. Recuperado el 3 de diciembre de 2014 .
  12. ^ ab "Señales de chirrido". dspguide.com . Consultado el 3 de diciembre de 2014 .
  13. ^ ab Nikitin, Alexei V.; Davidchack, Ruslan L. (2019). "El ancho de banda no es suficiente: ruido atípico "oculto" y su mitigación". arXiv : 1907.04186 [eess.SP].
  14. ^ Manual de radioaficionado para principiantes Por Clay Laster
Wikimedia Commons alberga una categoría multimedia sobre Chirp .
Busque chirrido en Wikcionario, el diccionario libre.
  • Generador de tonos de chirrido en línea (salida en archivo WAV)
  • Sonda CHIRP en FishFinder
  • Sonda CHIRP en FishFinder
Retrieved from "https://en.wikipedia.org/w/index.php?title=Chirp&oldid=1230749142"