De cadena

En física y geometría , una catenaria ( EE. UU .: / ˈkætənɛri / KAT - ən-err-ee , Reino Unido : / kəˈt iːnəri / kə - TEE -nər-ee ) es la curva que asume una cadena o un cable colgante idealizado bajo su propio peso cuando se apoya solo en sus extremos en un campo gravitacional uniforme .

La curva catenaria tiene forma de U, superficialmente similar en apariencia a una parábola , lo cual no es.

La curva aparece en el diseño de ciertos tipos de arcos y como sección transversal del catenoide , la forma que asume una película de jabón delimitada por dos anillos circulares paralelos.

La catenaria también se denomina alisoide , cadena , ^[1] o, particularmente en las ciencias de los materiales, un ejemplo de funicular . ^[2] La estática de cuerdas describe las catenarias en un problema de estática clásico que involucra una cuerda colgante. ^[3]

Matemáticamente, la curva catenaria es el gráfico de la función coseno hiperbólico . La superficie de revolución de la curva catenaria, la catenoide , es una superficie mínima , específicamente una superficie mínima de revolución . Una cadena colgante asumirá una forma de energía potencial mínima que es una catenaria. ^[4] Galileo Galilei en 1638 discutió la catenaria en el libro Dos nuevas ciencias reconociendo que era diferente de una parábola . Las propiedades matemáticas de la curva catenaria fueron estudiadas por Robert Hooke en la década de 1670, y su ecuación fue derivada por Leibniz , Huygens y Johann Bernoulli en 1691.

Las catenarias y las curvas relacionadas se utilizan en arquitectura e ingeniería (por ejemplo, en el diseño de puentes y arcos para que las fuerzas no resulten en momentos de flexión). En la industria del petróleo y el gas en alta mar, "catenaria" se refiere a un tubo ascendente de catenaria de acero , una tubería suspendida entre una plataforma de producción y el lecho marino que adopta una forma aproximada de catenaria. En la industria ferroviaria se refiere al cableado aéreo que transfiere energía a los trenes. (Esto a menudo sostiene un cable de contacto, en cuyo caso no sigue una verdadera curva catenaria).

En óptica y electromagnetismo, las funciones coseno y seno hiperbólicos son soluciones básicas de las ecuaciones de Maxwell. ^[5] Los modos simétricos que consisten en dos ondas evanescentes formarían una forma catenaria. ^{[6] [7] [8]}

La palabra "catenaria" se deriva del latín catēna , que significa " cadena ". La palabra inglesa "catenary" se suele atribuir a Thomas Jefferson , ^{[9] [10]} quien escribió en una carta a Thomas Paine sobre la construcción de un arco para un puente:

Recientemente he recibido de Italia un tratado sobre el equilibrio de los arcos, del abad Mascheroni. Parece ser una obra muy científica. Aún no he tenido tiempo de ocuparme de ella, pero he descubierto que las conclusiones de sus demostraciones son que todas las partes de la catenaria están en perfecto equilibrio. ^[11]

Se dice a menudo ^[12] que Galileo pensaba que la curva de una cadena colgante era parabólica. Sin embargo, en su obra Dos nuevas ciencias (1638), Galileo escribió que una cuerda colgante es sólo una parábola aproximada, observando correctamente que esta aproximación mejora en precisión a medida que la curvatura se hace más pequeña y es casi exacta cuando la elevación es menor de 45°. ^[13] El hecho de que la curva seguida por una cadena no es una parábola fue demostrado por Joachim Jungius (1587-1657); este resultado fue publicado póstumamente en 1669. ^[12]

La aplicación de la catenaria a la construcción de arcos se atribuye a Robert Hooke , cuya "verdadera forma matemática y mecánica" en el contexto de la reconstrucción de la Catedral de San Pablo aludía a una catenaria. ^[14] Algunos arcos mucho más antiguos se aproximan a las catenarias, un ejemplo de los cuales es el Arco de Taq-i Kisra en Ctesifonte . ^[15]

En 1671, Hooke anunció a la Royal Society que había resuelto el problema de la forma óptima de un arco, y en 1675 publicó una solución cifrada como anagrama latino ^[16] en un apéndice a su Descripción de helioscopios, ^[17] donde escribió que había encontrado "una verdadera forma matemática y mecánica de todo tipo de arcos para la construcción". No publicó la solución a este anagrama ^[18] en vida, pero en 1705 su albacea la proporcionó como ut pendet continuum flexile, sic stabit contiguum rigidum inversum , que significa "Como cuelga un cable flexible, así, invertidas, se encuentran las piezas en contacto de un arco".

En 1691, Gottfried Leibniz , Christiaan Huygens y Johann Bernoulli derivaron la ecuación en respuesta a un desafío de Jakob Bernoulli ; ^[12] sus soluciones se publicaron en Acta Eruditorum de junio de 1691. ^{[19] [20]} David Gregory escribió un tratado sobre la catenaria en 1697 ^{[12] [21]} en el que proporcionó una derivación incorrecta de la ecuación diferencial correcta. ^[20]

Leonhard Euler demostró en 1744 que la catenaria es la curva que, cuando gira alrededor del eje x , da la superficie de área mínima (la catenoide ) para los círculos delimitadores dados. ^[1] Nicolas Fuss dio ecuaciones que describen el equilibrio de una cadena bajo cualquier fuerza en 1796. ^[22]

Los arcos catenarios se utilizan a menudo en la construcción de hornos . Para crear la curva deseada, la forma de una cadena colgante de las dimensiones deseadas se transfiere a un molde que luego se utiliza como guía para la colocación de ladrillos u otro material de construcción. ^{[23] [24]}

A veces se dice que el Gateway Arch en St. Louis, Missouri , Estados Unidos es una catenaria (invertida), pero esto es incorrecto. ^[25] Está cerca de una curva más general llamada catenaria aplanada, con ecuación y = A  cosh( Bx ) , que es una catenaria si AB = 1 . Si bien una catenaria es la forma ideal para un arco independiente de espesor constante, el Gateway Arch es más estrecho cerca de la parte superior. Según la nominación del arco como Monumento Histórico Nacional de los EE. UU. , es una " catenaria ponderada ". Su forma corresponde a la forma que tendría una cadena ponderada, con eslabones más ligeros en el medio. ^{[26] [27]}

• 
  Arcos de catenaria ^[28] bajo el techo de la Casa Milà de Gaudí , Barcelona , ​​España.
• 
  El jardín de invierno de Sheffield está rodeado por una serie de arcos catenarios . ^[29]
• 
  El Gateway Arch ( San Luis, Misuri ) es una catenaria aplanada.
• 
  Horno de arco catenario en construcción sobre encofrado provisional

En las cadenas colgantes, la fuerza ejercida es uniforme con respecto a la longitud de la cadena, y por lo tanto la cadena sigue la curva catenaria. ^[30] Lo mismo ocurre con un puente colgante simple o "puente catenario", donde la calzada sigue el cable. ^{[31] [32]}

Un puente de cinta estresado es una estructura más sofisticada con la misma forma de catenaria. ^{[33] [34]}

Sin embargo, en un puente colgante con una calzada suspendida, las cadenas o cables soportan el peso del puente, y por lo tanto no cuelgan libremente. En la mayoría de los casos la calzada es plana, por lo que cuando el peso del cable es insignificante en comparación con el peso que se sostiene, la fuerza ejercida es uniforme con respecto a la distancia horizontal, y el resultado es una parábola , como se analiza a continuación (aunque el término "catenaria" todavía se utiliza a menudo, en un sentido informal). Si el cable es pesado, la curva resultante está entre una catenaria y una parábola. ^{[35] [36]}

La catenaria producida por la gravedad proporciona una ventaja a los cabos de anclaje pesados. Un cabo de anclaje (o línea de anclaje) generalmente consta de cadena o cable o ambos. Los cabos de anclaje se utilizan en barcos, plataformas petrolíferas, muelles, turbinas eólicas flotantes y otros equipos marinos que deben anclarse al fondo del mar.

Cuando la cuerda está floja, la curva catenaria presenta un ángulo de tracción menor sobre el ancla o dispositivo de amarre que si estuviera casi recta. Esto mejora el rendimiento del ancla y aumenta el nivel de fuerza que resistirá antes de arrastrarse. Para mantener la forma catenaria en presencia de viento, se necesita una cadena pesada, de modo que solo los barcos más grandes en aguas más profundas pueden confiar en este efecto. Los barcos más pequeños también dependen de la catenaria para mantener la máxima capacidad de sujeción. ^[37]

Los transbordadores de cable y los barcos de cadena representan un caso especial de vehículos marinos que se mueven aunque estén amarrados por dos catenarias, cada una de las cuales está formada por uno o más cables (cables de acero o cadenas) que pasan a través del vehículo y se mueven mediante poleas motorizadas. Las catenarias se pueden evaluar gráficamente. ^[38]

La ecuación de una catenaria en coordenadas cartesianas tiene la forma ^[35]

$${\displaystyle y=a\cosh \left({\frac {x}{a}}\right)={\frac {a}{2}}\left(e^{\frac {x}{a}}+e^{-{\frac {x}{a}}}\right),}$$donde cosh es la función coseno hiperbólico , y donde a es la distancia del punto más bajo por encima del eje x. ^[39] Todas las curvas catenarias son similares entre sí, ya que cambiar el parámetro a es equivalente a una escala uniforme de la curva.

La ecuación de Whewell para la catenaria es ^[35] donde es el ángulo tangencial y s la longitud del arco .$${\displaystyle \tan \varphi ={\frac {s}{a}},}$$${\estilo de visualización \varphi}$

Derivando y eliminando se obtiene la ecuación de Cesàro ^[40] donde es la curvatura .$${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos ^{2}\varphi }{a}},}$$${\estilo de visualización \varphi}$$${\displaystyle \kappa ={\frac {a}{s^{2}+a^{2}}},}$$${\estilo de visualización \kappa}$

El radio de curvatura es entonces la longitud de la normal entre la curva y el eje x . ^[41]$${\displaystyle \rho = a\sec ^{2}\varphi ,}$$

Cuando se hace rodar una parábola a lo largo de una línea recta, la curva de ruleta trazada por su foco es una catenaria. ^[42] La envolvente de la directriz de la parábola también es una catenaria. ^[43] La involuta desde el vértice, es decir, la ruleta trazada por un punto que comienza en el vértice cuando se hace rodar una línea sobre una catenaria, es la tractriz . ^[42]

Otra ruleta, formada al rodar una línea sobre una catenaria, es otra línea. Esto implica que las ruedas cuadradas pueden rodar perfectamente sin problemas sobre una carretera formada por una serie de baches en forma de una curva catenaria invertida. Las ruedas pueden ser cualquier polígono regular excepto un triángulo, pero la catenaria debe tener parámetros correspondientes a la forma y dimensiones de las ruedas. ^[44]

En cualquier intervalo horizontal, la relación entre el área bajo la catenaria y su longitud es igual a , independientemente del intervalo seleccionado. La catenaria es la única curva plana, aparte de una línea horizontal, que posee esta propiedad. Además, el centroide geométrico del área bajo un tramo de catenaria es el punto medio del segmento perpendicular que conecta el centroide de la propia curva y el eje x . ^[45]

Una carga en movimiento en un campo eléctrico uniforme viaja a lo largo de una catenaria (que tiende a una parábola si la velocidad de la carga es mucho menor que la velocidad de la luz c ). ^[46]

La superficie de revolución con radios fijos en cada extremo que tiene un área superficial mínima es una catenaria que gira alrededor del eje x . ^[42]

En el modelo matemático, la cadena (o cuerda, cable, soga, cordel, etc.) se idealiza asumiendo que es tan delgada que puede considerarse como una curva y que es tan flexible que cualquier fuerza de tensión ejercida por la cadena es paralela a la cadena. ^[47] El análisis de la curva para un arco óptimo es similar excepto que las fuerzas de tensión se convierten en fuerzas de compresión y todo se invierte. ^[48] Un principio subyacente es que la cadena puede considerarse un cuerpo rígido una vez que ha alcanzado el equilibrio. ^[49] Las ecuaciones que definen la forma de la curva y la tensión de la cadena en cada punto pueden derivarse mediante una inspección cuidadosa de las diversas fuerzas que actúan sobre un segmento utilizando el hecho de que estas fuerzas deben estar en equilibrio si la cadena está en equilibrio estático .

Sea el camino seguido por la cadena dado paramétricamente por r = ( x , y ) = ( x ( s ), y ( s )) donde s representa la longitud del arco y r es el vector de posición . Esta es la parametrización natural y tiene la propiedad de que

$${\displaystyle {\frac {d\mathbf {r} }{ds}}=\mathbf {u} }$$

donde u es un vector tangente unitario .

Se puede derivar una ecuación diferencial para la curva de la siguiente manera. ^[50] Sea c el punto más bajo de la cadena, llamado vértice de la catenaria. ^[51] La pendiente ⁠morir/Dx⁠ de la curva es cero en c ya que es un punto mínimo. Suponga que r está a la derecha de c ya que el otro caso está implícito por simetría. Las fuerzas que actúan sobre la sección de la cadena de c a r son la tensión de la cadena en c , la tensión de la cadena en r y el peso de la cadena. La tensión en c es tangente a la curva en c y, por lo tanto, es horizontal sin ningún componente vertical y tira de la sección hacia la izquierda, por lo que puede escribirse (− T ₀ , 0) donde T ₀ es la magnitud de la fuerza. La tensión en r es paralela a la curva en r y tira de la sección hacia la derecha. La tensión en r se puede dividir en dos componentes, por lo que puede escribirse T u = ( T cos φ , T sin φ ) , donde T es la magnitud de la fuerza y ​​φ es el ángulo entre la curva en r y eleje x (ver ángulo tangencial ). Finalmente, el peso de la cadena está representado por (0, − ws ) donde w es el peso por unidad de longitud y s es la longitud del segmento de cadena entre c y r .

La cadena está en equilibrio por lo que la suma de las tres fuerzas es 0 , por lo tanto

$${\displaystyle T\cos \varphi =T_{0}}$$y$${\displaystyle T\sin \varphi = ws\,,}$$

y dividiendo estos se obtiene

$${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {ws}{T_{0}}}\,.}$$

Es conveniente escribir

$${\displaystyle a={\frac {T_{0}}{w}}}$$

que es la longitud de la cadena cuyo peso es igual en magnitud a la tensión en c . ^[52] Entonces

$${\displaystyle {\frac {dy}{dx}}={\frac {s}{a}}}$$

es una ecuación que define la curva.

El componente horizontal de la tensión, T cos φ = T ₀ es constante y el componente vertical de la tensión, T sin φ = ws es proporcional a la longitud de la cadena entre r y el vértice. ^[53]

La ecuación diferencial , dada anteriormente, se puede resolver para producir ecuaciones para la curva. ^[54] Resolveremos la ecuación usando la condición de contorno de que el vértice está posicionado en y .${\displaystyle dy/dx=s/a}$${\displaystyle s_{0}=0}$${\ Displaystyle (x, y) = (x_ {0}, y_ {0})}$

Primero, invoque la fórmula para la longitud del arco para obtener las variables separadas y obtener$${\displaystyle {\frac {ds}{dx}}={\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}={\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}\,,}$$$${\displaystyle {\frac {ds}{\sqrt {1+(s/a)^{2}}}}=dx\,.}$$

Un enfoque razonablemente sencillo para integrar esto es utilizar la sustitución hiperbólica , que da (donde es una constante de integración ), y por lo tanto$${\displaystyle a\sinh ^{-1}{\frac {s}{a}}+x_{0}=x}$$$estilo de visualización x_{0}}$$${\displaystyle {\frac {s}{a}}=\sinh {\frac {x-x_{0}}{a}}\,.}$$

Pero , entonces, que integra como ( siendo la constante de integración que satisface la condición de contorno).${\textstyle s/a=dy/dx}$$${\displaystyle {\frac {dy}{dx}}=\sinh {\frac {x-x_{0}}{a}}\,,}$$$${\displaystyle y=a\cosh {\frac {x-x_{0}}{a}}+\delta }$$${\displaystyle \delta =y_{0}-a}$

Dado que el interés principal aquí es simplemente la forma de la curva, la ubicación de los ejes de coordenadas es arbitraria; por lo tanto, tome la decisión conveniente de simplificar el resultado a${\textstyle x_{0}=0=\delta }$$${\displaystyle y=a\cosh {\frac {x}{a}}\quad \square }$$

Para completar, la relación se puede derivar resolviendo cada una de las relaciones y para , obteniendo: por lo que se puede reescribir como${\displaystyle y\leftrightarrow s}$${\displaystyle x\leftrightarrow y}$${\displaystyle x\flecha izquierda derecha s}$${\estilo de visualización x/a}$$${\displaystyle \cosh ^{-1}{\frac {y-\delta }{a}}={\frac {x-x_{0}}{a}}=\sinh ^{-1}{\frac {s}{a}}\,,}$$$${\displaystyle y-\delta =a\cosh \left(\sinh ^{-1}{\frac {s}{a}}\right)\,,}$$$${\displaystyle y-\delta =a{\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}={\sqrt {a^{2}+s^{2}}}\,.}$$

La ecuación diferencial se puede resolver utilizando un enfoque diferente. [ ^55]

$${\displaystyle s=a\tan \varphi }$$

resulta que

$${\displaystyle {\frac {dx}{d\varphi }}={\frac {dx}{ds}}{\frac {ds}{d\varphi }}=\cos \varphi \cdot a\sec ^{ 2}\varphi =a\sec \varphi }$$y$${\displaystyle {\frac {dy}{d\varphi }}={\frac {dy}{ds}}{\frac {ds}{d\varphi }}=\sin \varphi \cdot a\sec ^{ 2}\varphi =a\tan \varphi \sec \varphi \,.}$$

La integración da,

$${\displaystyle x=a\ln(\sec \varphi +\tan \varphi )+\alpha }$$y$${\displaystyle y=a\sec \varphi +\beta \,.}$$

Como antes, los ejes x e y se pueden desplazar de modo que α y β se puedan tomar como 0. Entonces

$${\displaystyle \sec \varphi +\tan \varphi =e^{\frac {x}{a}}\,,}$$y tomando el recíproco de ambos lados$${\displaystyle \sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}}\,.}$$

Sumando y restando las dos últimas ecuaciones obtenemos la solución y$${\displaystyle y=a\sec \varphi =a\cosh \left({\frac {x}{a}}\right)\,,}$$$${\displaystyle s=a\tan \varphi =a\sinh \left({\frac {x}{a}}\right)\,.}$$

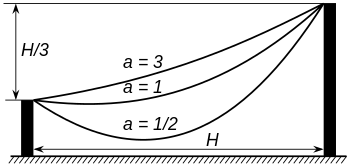
En general, el parámetro a es la posición del eje. La ecuación se puede determinar en este caso de la siguiente manera: ^[56]

Si es necesario, vuelva a etiquetar de modo que P ₁ esté a la izquierda de P ₂ y sea H la distancia horizontal y v la distancia vertical de P ₁ a P _2. Traslade los ejes de modo que el vértice de la catenaria se encuentre en el eje y y su altura a se ajuste de modo que la catenaria satisfaga la ecuación estándar de la curva .

$${\displaystyle y=a\cosh \left({\frac {x}{a}}\right)}$$

y sean las coordenadas de P ₁ y P ₂ ( x ₁ , y ₁ ) y ( x ₂ , y ₂ ) respectivamente. La curva pasa por estos puntos, por lo que la diferencia de altura es

$${\displaystyle v=a\cosh \left({\frac {x_{2}}{a}}\right)-a\cosh \left({\frac {x_{1}}{a}}\right)\,.}$$

y la longitud de la curva de P ₁ a P ₂ es

$${\displaystyle L=a\sinh \left({\frac {x_{2}}{a}}\right)-a\sinh \left({\frac {x_{1}}{a}}\right)\,.}$$

Cuando L ² − v ² se desarrolla utilizando estas expresiones el resultado es

$${\displaystyle L^{2}-v^{2}=2a^{2}\left(\cosh \left({\frac {x_{2}-x_{1}}{a}}\right)-1\right)=4a^{2}\sinh ^{2}\left({\frac {H}{2a}}\right)\,,}$$entonces$${\displaystyle {\frac {1}{H}}{\sqrt {L^{2}-v^{2}}}={\frac {2a}{H}}\sinh \left({\frac {H}{2a}}\right)\,.}$$

Esta es una ecuación trascendental en a y debe resolverse numéricamente . Dado que es estrictamente monótona en , ^[57] hay como máximo una solución con a > 0 y, por lo tanto, hay como máximo una posición de equilibrio.${\displaystyle \sinh(x)/x}$${\displaystyle x>0}$

Sin embargo, si ambos extremos de la curva ( P ₁ y P ₂ ) están al mismo nivel ( y ₁ = y ₂ ), se puede demostrar que ^[58] donde L es la longitud total de la curva entre P ₁ y P ₂ y h es la flecha (distancia vertical entre P ₁ , P ₂ y el vértice de la curva).$${\displaystyle a={\frac {{\frac {1}{4}}L^{2}-h^{2}}{2h}}\,}$$

También se puede demostrar que y donde H es la distancia horizontal entre P ₁ y P ₂ que se encuentran en el mismo nivel ( H = x ₂ − x ₁ ).$${\displaystyle L=2a\sinh {\frac {H}{2a}}\,}$$$${\displaystyle H=2a\operatorname {arcosh} {\frac {h+a}{a}}\,}$$

La fuerza de tracción horizontal en P ₁ y P ₂ es T ₀ = wa , donde w es el peso por unidad de longitud de la cadena o cable.

Existe una relación simple entre la tensión en el cable en un punto y su coordenada x y/o y . Comience combinando los cuadrados de los componentes vectoriales de la tensión: que (recordando que ) se puede reescribir como Pero, como se muestra arriba, (suponiendo que ), entonces obtenemos las relaciones simples ^[59]$${\displaystyle (T\cos \varphi )^{2}+(T\sin \varphi )^{2}=T_{0}^{2}+(ws)^{2}}$$${\displaystyle T_{0}=wa}$$${\displaystyle {\begin{aligned}T^{2}(\cos ^{2}\varphi +\sin ^{2}\varphi )&=(wa)^{2}+(ws)^{2}\\[6pt]T^{2}&=w^{2}(a^{2}+s^{2})\\[6pt]T&=w{\sqrt {a^{2}+s^{2}}}\,.\end{aligned}}}$$${\displaystyle y={\sqrt {a^{2}+s^{2}}}}$${\displaystyle y_{0}=a}$$${\displaystyle T=wy=wa\cosh {\frac {x}{a}}\,.}$$

Consideremos una cadena de longitud suspendida de dos puntos de igual altura y a una distancia . La curva tiene que minimizar su energía potencial (donde w es el peso por unidad de longitud) y está sujeta a la restricción ${\displaystyle L}$${\displaystyle D}$$${\displaystyle U=\int _{0}^{D}wy{\sqrt {1+y'^{2}}}dx}$$$${\displaystyle \int _{0}^{D}{\sqrt {1+y'^{2}}}dx=L\,.}$$

Por tanto, el lagrangiano modificado es donde es el multiplicador de Lagrange que se desea determinar. Como la variable independiente no aparece en el lagrangiano, podemos utilizar la identidad de Beltrami donde es una constante de integración, para obtener una primera integral.$${\displaystyle {\mathcal {L}}=(wy-\lambda ){\sqrt {1+y'^{2}}}}$$${\displaystyle \lambda }$${\displaystyle x}$ $${\displaystyle {\mathcal {L}}-y'{\frac {\partial {\mathcal {L}}}{\partial y'}}=C}$$${\displaystyle C}$$${\displaystyle {\frac {(wy-\lambda )}{\sqrt {1+y'^{2}}}}=-C}$$

Se trata de una ecuación diferencial ordinaria de primer orden que se puede resolver mediante el método de separación de variables . Su solución es el coseno hiperbólico habitual donde los parámetros se obtienen a partir de las restricciones.

Si la densidad de la cadena es variable, entonces el análisis anterior se puede adaptar para producir ecuaciones para la curva dada la densidad, o dada la curva para encontrar la densidad. ^[60]

Sea w el peso por unidad de longitud de la cadena, entonces el peso de la cadena tiene magnitud

$${\displaystyle \int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,}$$

donde los límites de integración son c y r . Al equilibrar las fuerzas como en la cadena uniforme se produce

$${\displaystyle T\cos \varphi =T_{0}}$$y por lo tanto$${\displaystyle T\sin \varphi =\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,}$$$${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {1}{T_{0}}}\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,.}$$

La diferenciación entonces da

$${\displaystyle w=T_{0}{\frac {d}{ds}}{\frac {dy}{dx}}={\frac {T_{0}{\dfrac {d^{2}y}{dx^{2}}}}{\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}}\,.}$$

En términos de φ y el radio de curvatura ρ esto se convierte en

$${\displaystyle w={\frac {T_{0}}{\rho \cos ^{2}\varphi }}\,.}$$

Se puede realizar un análisis similar para encontrar la curva que sigue el cable que sostiene un puente colgante con una calzada horizontal. ^[61] Si el peso de la calzada por unidad de longitud es w y el peso del cable y del alambre que sostienen el puente es despreciable en comparación, entonces el peso sobre el cable (ver la figura en Catenaria#Modelo de cadenas y arcos) desde c hasta r es wx donde x es la distancia horizontal entre c y r . Procediendo como antes se obtiene la ecuación diferencial

$${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,.}$$

Esto se resuelve mediante una integración simple para obtener

$${\displaystyle y={\frac {w}{2T_{0}}}x^{2}+\beta }$$

y así el cable sigue una parábola. Si el peso del cable y de los alambres que lo sostienen no es despreciable, entonces el análisis es más complejo. ^[62]

En una catenaria de igual resistencia, el cable se refuerza de acuerdo con la magnitud de la tensión en cada punto, por lo que su resistencia a la rotura es constante a lo largo de su longitud. Suponiendo que la resistencia del cable es proporcional a su densidad por unidad de longitud, el peso, w , por unidad de longitud de la cadena se puede escribir ⁠yo/do⁠ , donde c es constante, y se puede aplicar el análisis para cadenas no uniformes. ^[63]

En este caso las ecuaciones para la tensión son

$${\displaystyle {\begin{aligned}T\cos \varphi &=T_{0}\,,\\T\sin \varphi &={\frac {1}{c}}\int T\,ds\,.\end{aligned}}}$$

Combinando da

$${\displaystyle c\tan \varphi =\int \sec \varphi \,ds}$$

y por diferenciación

$${\displaystyle c=\rho \cos \varphi }$$

donde ρ es el radio de curvatura.

La solución a esto es

$${\displaystyle y=c\ln \left(\sec \left({\frac {x}{c}}\right)\right)\,.}$$

En este caso, la curva tiene asíntotas verticales y esto limita el rango a π c . Otras relaciones son

$${\displaystyle x=c\varphi \,,\quad s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}}\right)\right)\,.}$$

La curva fue estudiada en 1826 por Davies Gilbert y, aparentemente de forma independiente, por Gaspard-Gustave Coriolis en 1836.

Recientemente, se demostró que este tipo de catenaria podría actuar como un bloque de construcción de metasuperficie electromagnética y se conoció como "catenaria de gradiente de fase igual". ^[64]

En una catenaria elástica , la cadena se reemplaza por un resorte que puede estirarse en respuesta a la tensión. Se supone que el resorte se estira de acuerdo con la Ley de Hooke . Específicamente, si p es la longitud natural de una sección de resorte, entonces la longitud del resorte con la tensión T aplicada tiene una longitud

$${\displaystyle s=\left(1+{\frac {T}{E}}\right)p\,,}$$

donde E es una constante igual a kp , donde k es la rigidez del resorte. ^[65] En la catenaria el valor de T es variable, pero la relación sigue siendo válida a nivel local, por lo que ^[66] La curva seguida por un resorte elástico ahora se puede derivar siguiendo un método similar al del resorte inelástico. ^[67]$${\displaystyle {\frac {ds}{dp}}=1+{\frac {T}{E}}\,.}$$

Las ecuaciones para la tensión del resorte son

$${\displaystyle T\cos \varphi =T_{0}\,,}$$y$${\displaystyle T\sin \varphi =w_{0}p\,,}$$

De donde

$${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {w_{0}p}{T_{0}}}\,,\quad T={\sqrt {T_{0}^{2}+w_{0}^{2}p^{2}}}\,,}$$

donde p es la longitud natural del segmento de c a r y w ₀ es el peso por unidad de longitud del resorte sin tensión. Escribe así$${\displaystyle a={\frac {T_{0}}{w_{0}}}}$$$${\displaystyle {\frac {dy}{dx}}=\tan \varphi ={\frac {p}{a}}\quad {\text{and}}\quad T={\frac {T_{0}}{a}}{\sqrt {a^{2}+p^{2}}}\,.}$$

Entonces de donde$${\displaystyle {\begin{aligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}{T}}\\[6pt]{\frac {dy}{ds}}&=\sin \varphi ={\frac {w_{0}p}{T}}\,,\end{aligned}}}$$$${\displaystyle {\begin{alignedat}{3}{\frac {dx}{dp}}&={\frac {T_{0}}{T}}{\frac {ds}{dp}}&&=T_{0}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {a}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}}{E}}\\[6pt]{\frac {dy}{dp}}&={\frac {w_{0}p}{T}}{\frac {ds}{dp}}&&={\frac {T_{0}p}{a}}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {p}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}p}{Ea}}\,.\end{alignedat}}}$$

La integración da las ecuaciones paramétricas

$${\displaystyle {\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p+\alpha \,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}+\beta \,.\end{aligned}}}$$

Nuevamente, los ejes x e y se pueden desplazar de modo que α y β se pueden tomar como 0. Por lo tanto,

$${\displaystyle {\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p\,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}\end{aligned}}}$$

son ecuaciones paramétricas para la curva. En el límite rígido donde E es grande, la forma de la curva se reduce a la de una cadena no elástica.

Sin hacer suposiciones sobre la fuerza G que actúa sobre la cadena, se puede realizar el siguiente análisis. ^[68]

En primer lugar, sea T = T ( s ) la fuerza de tensión en función de s . La cadena es flexible, por lo que solo puede ejercer una fuerza paralela a sí misma. Como la tensión se define como la fuerza que la cadena ejerce sobre sí misma, T debe ser paralela a la cadena. En otras palabras,

$${\displaystyle \mathbf {T} =T\mathbf {u} \,,}$$

donde T es la magnitud de T y u es el vector tangente unitario.

En segundo lugar, sea G = G ( s ) la fuerza externa por unidad de longitud que actúa sobre un pequeño segmento de una cadena en función de s . Las fuerzas que actúan sobre el segmento de la cadena entre s y s + Δ s son la fuerza de tensión T ( s + Δ s ) en un extremo del segmento, la fuerza casi opuesta − T ( s ) en el otro extremo y la fuerza externa que actúa sobre el segmento que es aproximadamente G Δ s . Estas fuerzas deben equilibrarse de modo que

$${\displaystyle \mathbf {T} (s+\Delta s)-\mathbf {T} (s)+\mathbf {G} \Delta s\approx \mathbf {0} \,.}$$

Dividir por Δ s y tomar el límite cuando Δ s → 0 para obtener

$${\displaystyle {\frac {d\mathbf {T} }{ds}}+\mathbf {G} =\mathbf {0} \,.}$$

Estas ecuaciones se pueden utilizar como punto de partida en el análisis de una cadena flexible que actúa bajo cualquier fuerza externa. En el caso de la catenaria estándar, G = (0, − w ) donde la cadena tiene un peso w por unidad de longitud.

• Arco catenario
• Fuente de cadena o cuentas auto-sifonantes
• Catenaria aérea : líneas eléctricas suspendidas sobre vehículos ferroviarios o tranvías.
• Ruleta (curva) : una catenaria elíptica/hiperbólica
• Troposkein : la forma de una cuerda hilada
• Catenaria ponderada

• Lockwood, EH (1961). "Capítulo 13: La tractriz y la catenaria". Un libro de curvas . Cambridge.
• Salmon, George (1879). Curvas en planos superiores. Hodges, Foster y Figgis. págs. 287–289.
• Routh, Edward John (1891). "Capítulo X: Sobre cuerdas". Tratado sobre estática analítica . University Press.
• Maurer, Edward Rose (1914). "Art. 26 Cable catenario". Mecánica técnica . J. Wiley & Sons.
• Lamb, Sir Horace (1897). "Art. 134 Curvas trascendentales; catenaria, tractriz". Un curso elemental de cálculo infinitesimal . Prensa universitaria.
• Todhunter, Isaac (1858). "XI Cuerdas flexibles. Inextensibles, XII Cuerdas flexibles. Extensibles". Tratado de estática analítica . Macmillan.
• Whewell, William (1833). "Capítulo V: El equilibrio de un cuerpo flexible". Estática analítica . J. & JJ Deighton. pág. 65.
• Weisstein, Eric W. "Catenaria". MathWorld .

• Swetz, Frank (1995). Aprenda de los maestros. MAA. pp. 128–9. ISBN 978-0-88385-703-8.
• Venturoli, Giuseppe (1822). "Capítulo XXIII: Sobre la catenaria". Elementos de la teoría de la mecánica . Trad. Daniel Cresswell. J. Nicholson & Son.

Wikimedia Commons alberga una categoría multimedia sobre Catenaria .

Wikiquote tiene citas relacionadas con Catenaria .

Wikisource tiene el texto del artículo " Catenaria " de la Encyclopædia Britannica de 1911 .

• O'Connor, John J.; Robertson, Edmund F. , "Catenary", Archivo de Historia de las Matemáticas de MacTutor , Universidad de St Andrews
• Catenaria en PlanetMath .
• Calculadora de curva catenaria
• Catenaria en el Centro de Geometría
• "Catenaria" en el Diccionario visual de curvas planas especiales
• La Catenaria - Cadenas, Arcos y Películas de Jabón.
• Calculadora de error de flecha de cable: calcula la desviación de una línea recta de una curva catenaria y proporciona derivación de la calculadora y referencias.
• Se derivan las ecuaciones de curvas de centenarios tanto dinámicas como estáticas: se derivan las ecuaciones que rigen la forma (caso estático) y la dinámica (caso dinámico) de un centenario. Se analiza la solución de las ecuaciones.
• La línea recta, la catenaria, la braquistócrona, el círculo y el enfoque unificado de Fermat para algunas geodésicas.
• Ira Freeman "Una forma general de la catenaria de un puente colgante" Boletín de la AMS