Región de agotamiento

En física de semiconductores , la región de agotamiento , también llamada capa de agotamiento , zona de agotamiento , región de unión , región de carga espacial o capa de carga espacial , es una región aislante dentro de un material semiconductor conductor y dopado donde los portadores de carga móviles se han difundido o expulsados ​​por un campo eléctrico . Los únicos elementos que quedan en la región de agotamiento son impurezas donantes o aceptoras ionizadas. Esta región de iones positivos y negativos descubiertos se llama región de agotamiento debido al agotamiento de portadores en esta región, sin dejar ninguno para transportar una corriente. Comprender la región de agotamiento es clave para explicar la electrónica de semiconductores moderna : diodos , transistores de unión bipolar , transistores de efecto de campo y diodos de capacitancia variable dependen todos de fenómenos de región de agotamiento.

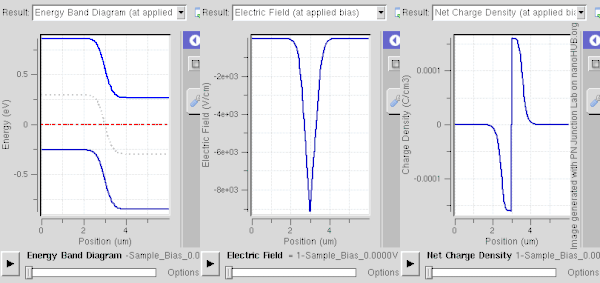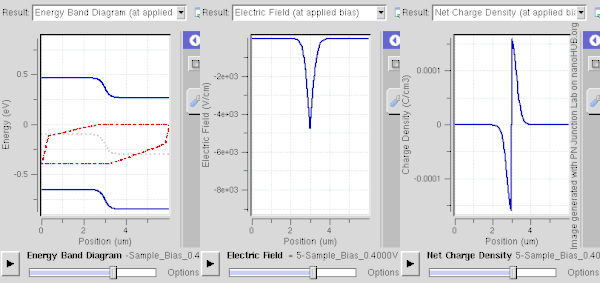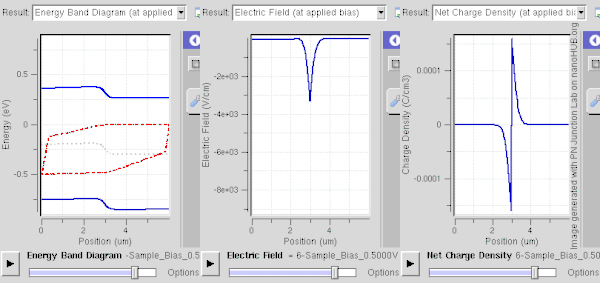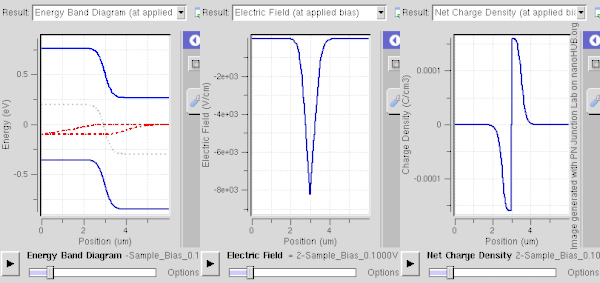
Una región de agotamiento se forma instantáneamente a través de una unión p–n . Se describe más fácilmente cuando la unión está en equilibrio térmico o en un estado estable : en ambos casos, las propiedades del sistema no varían en el tiempo; están en equilibrio dinámico . ^{[1] [2]}

Los electrones y los huecos se difunden en regiones con concentraciones más bajas de ellos, de forma muy similar a como la tinta se difunde en el agua hasta que se distribuye uniformemente. Por definición, el semiconductor de tipo N tiene un exceso de electrones libres (en la banda de conducción ) en comparación con el semiconductor de tipo P , y el tipo P tiene un exceso de huecos (en la banda de valencia ) en comparación con el tipo N. Por lo tanto, cuando los semiconductores dopados con N y dopados con P se colocan juntos para formar una unión, los electrones libres en la banda de conducción del lado N migran (se difunden) a la banda de conducción del lado P, y los huecos en la banda de valencia del lado P migran a la banda de valencia del lado N.

Después de la transferencia, los electrones difundidos entran en contacto con huecos y son eliminados por recombinación en el lado P. Del mismo modo, los huecos difundidos se recombinan con electrones libres así eliminados en el lado N. El resultado neto es que los electrones difundidos y los huecos desaparecen. En una región del lado N cerca de la interfaz de unión, los electrones libres en la banda de conducción desaparecen debido a (1) la difusión de electrones al lado P y (2) la recombinación de electrones a huecos que se difunden desde el lado P. Los huecos en una región del lado P cerca de la interfaz también desaparecen por una razón similar. Como resultado, los portadores de carga mayoritarios (electrones libres para el semiconductor de tipo N y huecos para el semiconductor de tipo P) se agotan en la región alrededor de la interfaz de unión, por lo que esta región se llama región de agotamiento o zona de agotamiento . Debido a la difusión del portador de carga mayoritario descrita anteriormente, la región de agotamiento está cargada; el lado N de la misma está cargado positivamente y el lado P está cargado negativamente. Esto crea un campo eléctrico que proporciona una fuerza que se opone a la difusión de la carga. Cuando el campo eléctrico es lo suficientemente fuerte como para detener la difusión de huecos y electrones, la región de agotamiento alcanza el equilibrio. La integración del campo eléctrico a lo largo de la región de agotamiento determina lo que se denomina voltaje incorporado (también llamado voltaje de unión o voltaje de barrera o potencial de contacto ).

Físicamente hablando, la transferencia de carga en dispositivos semiconductores se produce a partir de (1) la deriva del portador de carga por el campo eléctrico y (2) la difusión del portador de carga debido a la concentración de portadores que varía espacialmente. En el lado P de la región de agotamiento, donde los huecos se desplazan por el campo eléctrico con la conductividad eléctrica σ y se difunden con la constante de difusión D , la densidad de corriente neta está dada por

${\displaystyle {\bf {J}}=\sigma {\bf {E}}-eD\nabla p}$,

donde es el campo eléctrico, e es la carga elemental (1,6×10 ⁻¹⁹ coulomb), y p es la densidad de huecos (número por unidad de volumen). El campo eléctrico hace que los huecos se desplacen a lo largo de la dirección del campo, y para la difusión los huecos se mueven en la dirección de concentración decreciente, por lo que para los huecos resulta una corriente negativa para un gradiente de densidad positivo. (Si los portadores son electrones, la densidad de huecos p se reemplaza por la densidad de electrones n con signo negativo; en algunos casos, se deben incluir tanto electrones como huecos.) Cuando los dos componentes de la corriente se equilibran, como en la región de agotamiento de la unión p–n en equilibrio dinámico , la corriente es cero debido a la relación de Einstein , que relaciona D con σ .${\displaystyle {\bf {E}}}$

La polarización directa (aplicar un voltaje positivo al lado P con respecto al lado N) estrecha la región de agotamiento y reduce la barrera a la inyección de portadores (mostrado en la figura de la derecha). En más detalle, los portadores mayoritarios obtienen algo de energía del campo de polarización, lo que les permite entrar en la región y neutralizar cargas opuestas. Cuanto mayor sea la polarización, mayor neutralización (o apantallamiento de iones en la región) ocurre. Los portadores se pueden recombinar con los iones, pero la energía térmica hace que los portadores recombinados vuelvan a la transición anterior, ya que la energía de Fermi está cerca. Cuando la polarización es lo suficientemente fuerte como para que la región de agotamiento se vuelva muy delgada, el componente de difusión de la corriente (a través de la interfaz de la unión) aumenta en gran medida y el componente de deriva disminuye. En este caso, la corriente neta fluye desde el lado P al lado N. La densidad de portadores es grande (varía exponencialmente con el voltaje de polarización aplicado), lo que hace que la unión sea conductora y permita una gran corriente directa. ^[3] La descripción matemática de la corriente la proporciona la ecuación del diodo de Shockley . La baja corriente conducida bajo polarización inversa y la gran corriente bajo polarización directa es un ejemplo de rectificación .

En caso de polarización inversa (aplicando un voltaje negativo al lado P con respecto al lado N), la caída de potencial (es decir, el voltaje) a través de la región de agotamiento aumenta. Básicamente, los portadores mayoritarios son empujados lejos de la unión, dejando atrás más iones cargados. Por lo tanto, la región de agotamiento se ensancha y su campo se vuelve más fuerte, lo que aumenta el componente de deriva de la corriente (a través de la interfaz de la unión) y disminuye el componente de difusión. En este caso, la corriente neta fluye desde el lado N al lado P. La densidad de portadores (en su mayoría, portadores minoritarios) es pequeña y solo fluye una corriente de saturación inversa muy pequeña.

A partir de un análisis de agotamiento total como el que se muestra en la figura 2, la carga se aproximaría a una caída repentina en sus puntos límite que en realidad es gradual y se explica por la ecuación de Poisson . La cantidad de densidad de flujo sería entonces ^[4]

${\displaystyle {\begin{aligned}{\frac {Q_{n}}{x_{n}}}&=qN_{d}\\{\frac {Q_{p}}{x_{p}}}&=-qN_{a}\\\end{aligned}}}$

donde y son la cantidad de carga negativa y positiva respectivamente, y son la distancia para la carga negativa y positiva respectivamente con cero en el centro, y son la cantidad de átomos aceptores y donadores respectivamente y es la carga del electrón .${\displaystyle Q_{n}}$${\displaystyle Q_{p}}$$Estilo de visualización x_{n}$$estilo de visualización x_{p}}$$Estilo de visualización N_{a}$$Estilo de visualización N_{d}$${\estilo de visualización q}$

Al tomar la integral de la densidad de flujo con respecto a la distancia para determinar el campo eléctrico (es decir, la ley de Gauss ), se crea el segundo gráfico como se muestra en la figura 2:${\estilo de visualización D}$${\estilo de visualización dx}$${\estilo de visualización E}$

${\displaystyle E={\frac {\int D\,dx}{\epsilon _{s}}}}$

donde es la permitividad de la sustancia. La integración del campo eléctrico con respecto a la distancia determina el potencial eléctrico . Este también sería igual al voltaje incorporado, como se muestra en la Figura 2.${\displaystyle \epsilon_{s}}$${\estilo de visualización V}$${\displaystyle \Delta V}$

${\displaystyle V=\int Edx=\Delta V}$

La ecuación final se organizaría entonces de modo que la función del ancho de la capa de agotamiento dependería del potencial eléctrico .$Estilo de visualización x_{n}$${\estilo de visualización V}$

En resumen, y son el ancho de la capa de agotamiento negativo y positivo respectivamente con respecto al centro, y son la concentración de átomos aceptores y donadores respectivamente, es la carga del electrón y es el voltaje incorporado, que suele ser la variable independiente . ^[4]$Estilo de visualización x_{n}$$estilo de visualización x_{p}}$$Estilo de visualización N_{a}$$Estilo de visualización N_{d}$${\estilo de visualización q}$${\displaystyle \Delta V}$

Otro ejemplo de una región de agotamiento se da en el condensador MOS . Se muestra en la figura de la derecha, para un sustrato de tipo P. Supongamos que el semiconductor inicialmente es neutro en cuanto a carga, con la carga debida a los huecos exactamente equilibrada por la carga negativa debida a las impurezas dopantes del aceptor . Si ahora se aplica un voltaje positivo a la compuerta, lo que se hace introduciendo una carga positiva Q en la compuerta, entonces algunos huecos cargados positivamente en el semiconductor más cercano a la compuerta son repelidos por la carga positiva en la compuerta y salen del dispositivo a través del contacto inferior. Dejan atrás una región de agotamiento que es aislante porque no quedan huecos móviles; solo las impurezas del aceptor inmóviles y cargadas negativamente. Cuanto mayor sea la carga positiva colocada en la compuerta, más positivo será el voltaje de compuerta aplicado y más huecos saldrán de la superficie del semiconductor, agrandando la región de agotamiento. (En este dispositivo hay un límite en cuanto al ancho que puede alcanzar el agotamiento. Se establece mediante el inicio de una capa de inversión de portadores en una capa delgada, o canal , cerca de la superficie. La discusión anterior se aplica a voltajes positivos lo suficientemente bajos como para que no se forme una capa de inversión).

Si el material de la compuerta es polisilicio de tipo opuesto al semiconductor en masa, se forma una región de agotamiento espontáneo si la compuerta se pone en cortocircuito eléctricamente con el sustrato, de forma muy similar a la descrita para la unión p–n anterior. Para obtener más información sobre esto, consulte el efecto de agotamiento del polisilicio .

El principio de neutralidad de carga dice que la suma de cargas positivas debe ser igual a la suma de cargas negativas:

$${\displaystyle n+N_{A}=p+N_{D}\,,}$$

donde n y p son el número de electrones y huecos libres, y y son el número de donantes y aceptores ionizados "por unidad de longitud", respectivamente. De esta manera, tanto y pueden considerarse como densidades espaciales dopantes. Si suponemos una ionización completa y que , entonces:$Estilo de visualización N_ {D}}$$Estilo de visualización N_{A}$$Estilo de visualización N_ {D}}$$Estilo de visualización N_{A}$${\displaystyle n,p\ll N_{D},N_{A}}$

${\displaystyle qN_{A}w_{P}\aproximadamente qN_{D}w_{N}\,}$.

donde y son los anchos de depleción en el semiconductor p y n , respectivamente. Esta condición asegura que la carga neta negativa del aceptor equilibre exactamente la carga neta positiva del donante. El ancho de depleción total en este caso es la suma . En la referencia se presenta una derivación completa para el ancho de depleción. ^[5] Esta derivación se basa en resolver la ecuación de Poisson en una dimensión: la dimensión normal a la unión metalúrgica. El campo eléctrico es cero fuera del ancho de depleción (que se ve en la figura anterior) y, por lo tanto, la ley de Gauss implica que la densidad de carga en cada región se equilibra, como lo muestra la primera ecuación en esta subsección. Tratar cada región por separado y sustituir la densidad de carga para cada región en la ecuación de Poisson eventualmente conduce a un resultado para el ancho de depleción. Este resultado para el ancho de depleción es:$estilo de visualización wP$$Estilo de visualización w_{N}}$${\displaystyle w=w_{N}+w_{P}}$

$${\displaystyle w\approx \left[{\frac {2\epsilon _{r}\epsilon _{0}}{q}}\left({\frac {N_{A}+N_{D}}{N_{A}N_{D}}}\right)\left(V_{bi}-V\right)\right]^{\frac {1}{2}}}$$

donde es la permitividad dieléctrica relativa del semiconductor, es el voltaje incorporado y es la polarización aplicada. La región de agotamiento no está dividida simétricamente entre las regiones n y p - tenderá hacia el lado ligeramente dopado. ^[6] Un análisis más completo tendría en cuenta que todavía hay algunos portadores cerca de los bordes de la región de agotamiento. ^[7] Esto conduce a un término adicional de -2kT/q en el último conjunto de paréntesis anterior.${\displaystyle \epsilon _{r}}$${\displaystyle V_{bi}}$${\displaystyle V}$

Al igual que en las uniones p–n, el principio rector aquí es la neutralidad de carga. Supongamos un sustrato de tipo P. Si se coloca una carga positiva Q en la compuerta con área A , entonces los huecos se agotan hasta una profundidad w exponiendo suficientes aceptores negativos para equilibrar exactamente la carga de la compuerta. Suponiendo que la densidad del dopante sea de aceptores por unidad de volumen, entonces la neutralidad de carga requiere que el ancho de agotamiento w satisfaga la relación:${\displaystyle N_{A}}$

$${\displaystyle Q/A=qN_{A}w\,}$$

Si el ancho de empobrecimiento se vuelve lo suficientemente amplio, entonces los electrones aparecen en una capa muy delgada en la interfaz semiconductor-óxido, llamada capa de inversión porque tienen carga opuesta a los huecos que prevalecen en un material de tipo P. Cuando se forma una capa de inversión, el ancho de empobrecimiento deja de expandirse con el aumento de la carga de compuerta Q . En este caso, la neutralidad se logra atrayendo más electrones a la capa de inversión. En el MOSFET , esta capa de inversión se conoce como canal .

Asociado con la capa de agotamiento hay un efecto conocido como flexión de banda . Este efecto ocurre porque el campo eléctrico en la capa de agotamiento varía linealmente en el espacio desde su valor (máximo) en la compuerta hasta cero en el borde del ancho de agotamiento: ^[8]${\displaystyle E_{m}}$

${\displaystyle E_{m}={Q \over A\epsilon _{0}}=qN_{A}{w \over \epsilon _{0}},\,}$

donde  = 8,854×10 ⁻¹² F/m, F es el faradio y m es el metro. Este campo eléctrico que varía linealmente genera un potencial eléctrico que varía cuadráticamente en el espacio. Los niveles de energía, o bandas de energía, se curvan en respuesta a este potencial.${\displaystyle \epsilon _{0}}$

• Perfil de voltaje de capacitancia
• Estructura de metal-óxido-semiconductor
• Diodos semiconductores