Código de corrección de errores de ráfaga
En la teoría de codificación , los códigos de corrección de errores de ráfaga emplean métodos para corregir errores de ráfaga , que son errores que ocurren en muchos bits consecutivos en lugar de ocurrir en bits independientemente unos de otros.
Se han diseñado muchos códigos para corregir errores aleatorios . Sin embargo, a veces los canales pueden introducir errores que se localizan en un intervalo corto. Dichos errores se producen en ráfagas (denominados errores de ráfaga ) porque se producen en muchos bits consecutivos. Se pueden encontrar muchos ejemplos de errores de ráfaga en los medios de almacenamiento. Estos errores pueden deberse a daños físicos, como un rasguño en un disco o un rayo en el caso de los canales inalámbricos. No son independientes; tienden a estar concentrados espacialmente. Si un bit tiene un error, es probable que los bits adyacentes también puedan estar dañados. Los métodos utilizados para corregir errores aleatorios son ineficientes para corregir errores de ráfaga.
Definiciones

Una explosión de longitud ℓ [1]
Digamos que se transmite una palabra de código y se recibe como Entonces, el vector de error se denomina ráfaga de longitud si los componentes distintos de cero de están confinados a componentes consecutivos. Por ejemplo, es una ráfaga de longitud
Aunque esta definición es suficiente para describir qué es un error de ráfaga, la mayoría de las herramientas desarrolladas para la corrección de errores de ráfaga se basan en códigos cíclicos. Esto motiva nuestra siguiente definición.
Una ráfaga cíclica de longitud ℓ [1]
Un vector de error se denomina error de ráfaga cíclica de longitud si sus componentes distintos de cero están confinados a componentes cíclicamente consecutivos. Por ejemplo, el vector de error considerado anteriormente es una ráfaga cíclica de longitud , ya que consideramos que el error comienza en la posición y termina en la posición . Observe que los índices están basados en , es decir, el primer elemento está en la posición .
En el resto de este artículo, utilizaremos el término ráfaga para referirnos a una ráfaga cíclica, a menos que se indique lo contrario.
Descripción de la explosión
A menudo resulta útil tener una definición compacta de un error de ráfaga, que abarque no solo su longitud, sino también el patrón y la ubicación de dicho error. Definimos una descripción de ráfaga como una tupla donde es el patrón del error (es decir, la cadena de símbolos que comienza con la primera entrada distinta de cero en el patrón de error y termina con el último símbolo distinto de cero), y es la ubicación, en la palabra clave, donde se puede encontrar la ráfaga. [1]
Por ejemplo, la descripción de ráfaga del patrón de error es . Observe que dicha descripción no es única, porque describe el mismo error de ráfaga. En general, si el número de componentes distintos de cero en es , entonces tendrá diferentes descripciones de ráfaga, cada una comenzando en una entrada distinta de cero de . Sin embargo, para remediar los problemas que surgen por la ambigüedad de las descripciones de ráfaga con el teorema siguiente, antes de hacerlo necesitamos una definición.
Definición. El número de símbolos en un patrón de error dado se denota por
Teorema (Unicidad de las descripciones de ráfagas) : supongamos que es un vector de error de longitud con dos descripciones de ráfagas y . Si entonces las dos descripciones son idénticas, es decir, sus componentes son equivalentes. [2]
Sea el peso de Hamming (o el número de entradas distintas de cero) de . Entonces tiene exactamente descripciones de error. Porque no hay nada que demostrar. Por lo tanto, suponemos que y que las descripciones no son idénticas. Observamos que cada entrada distinta de cero de aparecerá en el patrón y, por lo tanto, los componentes de no incluidos en el patrón formarán una serie cíclica de ceros, comenzando después de la última entrada distinta de cero y continuando justo antes de la primera entrada distinta de cero del patrón. Llamamos serie cero al conjunto de índices correspondiente a esta serie. Observamos inmediatamente que cada descripción de ráfaga tiene una serie cero asociada y que cada serie cero es disjunta. Dado que tenemos series cero y cada una es disjunta, tenemos un total de elementos distintos en todas las series cero. Por otro lado, tenemos: Esto contradice Por lo tanto, las descripciones de error de ráfaga son idénticas.
Un corolario del teorema anterior es que no podemos tener dos descripciones de ráfagas distintas para ráfagas de longitud
Códigos cíclicos para la corrección de errores de ráfaga
Los códigos cíclicos se definen de la siguiente manera: piense en los símbolos como elementos en . Ahora, podemos pensar en las palabras como polinomios sobre donde los símbolos individuales de una palabra corresponden a los diferentes coeficientes del polinomio. Para definir un código cíclico, elegimos un polinomio fijo, llamado polinomio generador . Las palabras clave de este código cíclico son todos los polinomios que son divisibles por este polinomio generador.
Las palabras clave son polinomios de grado . Supongamos que el polinomio generador tiene grado . Los polinomios de grado que son divisibles por resultan de multiplicar por polinomios de grado . Tenemos tales polinomios. Cada uno de ellos corresponde a una palabra clave. Por lo tanto, para los códigos cíclicos.
Los códigos cíclicos pueden detectar todas las ráfagas de longitud hasta . Más adelante veremos que la capacidad de detección de errores de ráfaga de cualquier código está limitada desde arriba por . Los códigos cíclicos se consideran óptimos para la detección de errores de ráfaga ya que cumplen con este límite superior:
Teorema (capacidad de corrección de ráfagas cíclicas) : todo código cíclico con polinomio generador de grado puede detectar todas las ráfagas de longitud
Necesitamos demostrar que si agregas una ráfaga de longitud a una palabra de código (es decir, a un polinomio que es divisible por ), entonces el resultado no va a ser una palabra de código (es decir, el polinomio correspondiente no es divisible por ). Basta con demostrar que ninguna ráfaga de longitud es divisible por . Tal ráfaga tiene la forma , donde Por lo tanto, no es divisible por (porque este último tiene grado ). no es divisible por (De lo contrario, todas las palabras de código comenzarían con ). Por lo tanto, tampoco es divisible por .
La prueba anterior sugiere un algoritmo simple para la detección/corrección de errores de ráfaga en códigos cíclicos: dada una palabra transmitida (es decir, un polinomio de grado ), calcule el resto de esta palabra cuando se divide por . Si el resto es cero (es decir, si la palabra es divisible por ), entonces es una palabra de código válida. De lo contrario, informe un error. Para corregir este error, reste este resto de la palabra transmitida. El resultado de la resta será divisible por (es decir, será una palabra de código válida).
Por el límite superior de detección de error de ráfaga ( ), sabemos que un código cíclico no puede detectar todas las ráfagas de longitud . Sin embargo, los códigos cíclicos pueden detectar la mayoría de las ráfagas de longitud . La razón es que la detección falla solo cuando la ráfaga es divisible por . En los alfabetos binarios, existen ráfagas de longitud . De ellas, solo son divisibles por . Por lo tanto, la probabilidad de falla de detección es muy pequeña ( ) suponiendo una distribución uniforme en todas las ráfagas de longitud .
Ahora consideramos un teorema fundamental sobre códigos cíclicos que ayudará a diseñar códigos de corrección de errores de ráfagas eficientes, categorizando las ráfagas en diferentes clases laterales.
Teorema ( cosets distintos ) — Un código lineal es un código corrector de errores de ráfaga si todos los errores de ráfaga de longitud se encuentran en coconjuntos distintos de .
Sean errores de ráfaga distintos de longitud que se encuentran en la misma clase lateral del código . Entonces es una palabra de código. Por lo tanto, si recibimos podemos decodificarlo como o como . Por el contrario, si todos los errores de ráfaga y no se encuentran en la misma clase lateral, entonces cada error de ráfaga está determinado por su síndrome. El error puede entonces corregirse a través de su síndrome. Por lo tanto, un código lineal es un código corrector de errores de ráfaga si y solo si todos los errores de ráfaga de longitud se encuentran en clases laterales distintas de .
Teorema (Clasificación de palabras clave de error de ráfaga) : Sea un código de corrección de error de ráfaga lineal. Entonces, ninguna ráfaga de longitud distinta de cero puede ser una palabra clave.
Sea una palabra de código con una ráfaga de longitud . Por lo tanto, tiene el patrón , donde y son palabras de longitud Por lo tanto, las palabras y son dos ráfagas de longitud . Para los códigos lineales binarios, pertenecen a la misma clase lateral. Esto contradice el Teorema de clases laterales distintas, por lo tanto, ninguna ráfaga de longitud distinta de cero puede ser una palabra de código.
Límites de corrección de errores de ráfaga
Límites superiores para la detección y corrección de errores de ráfaga
Por límite superior, nos referimos a un límite en nuestra capacidad de detección de errores que nunca podemos ir más allá. Supongamos que queremos diseñar un código que pueda detectar todos los errores de ráfaga de longitud Una pregunta natural que nos hacemos es: dados y , ¿cuál es el máximo que nunca podemos alcanzar más allá? En otras palabras, ¿cuál es el límite superior en la longitud de las ráfagas que podemos detectar usando cualquier código? El siguiente teorema proporciona una respuesta a esta pregunta.
Teorema (capacidad de detección de errores de ráfaga) — La capacidad de detección de errores de ráfaga de cualquier código es
Primero observamos que un código puede detectar todas las ráfagas de longitud si y solo si no hay dos palabras de código que difieran en una ráfaga de longitud . Supongamos que tenemos dos palabras de código y que difieren en una ráfaga de longitud . Al recibir , no podemos saber si la palabra transmitida no tiene errores de transmisión o si tiene un error de ráfaga que ocurrió durante la transmisión. Ahora, supongamos que cada dos palabras de código difieren en más de una ráfaga de longitud Incluso si la palabra de código transmitida es golpeada por una ráfaga de longitud , no va a cambiar a otra palabra de código válida. Al recibirla, podemos decir que esto es con una ráfaga Por la observación anterior, sabemos que no hay dos palabras de código que puedan compartir los primeros símbolos. La razón es que incluso si difieren en todos los demás símbolos, seguirán siendo diferentes en una ráfaga de longitud Por lo tanto, el número de palabras de código satisface Aplicando a ambos lados y reordenando, podemos ver que .
Ahora, repetimos la misma pregunta pero para la corrección de errores: dados y , ¿cuál es el límite superior de la longitud de las ráfagas que podemos corregir utilizando cualquier código? El siguiente teorema proporciona una respuesta preliminar a esta pregunta:
Teorema (capacidad de corrección de errores en ráfaga) — La capacidad de corrección de errores en ráfaga de cualquier código satisface
Primero observamos que un código puede corregir todas las ráfagas de longitud si y solo si no hay dos palabras de código que difieran en la suma de dos ráfagas de longitud Supongamos que dos palabras de código y difieren en ráfagas y de longitud cada una. Al recibir el impacto de una ráfaga , podríamos interpretarlo como si hubiera sido afectado por una ráfaga . No podemos saber si la palabra transmitida es o . Ahora, supongamos que cada dos palabras de código difieren en más de dos ráfagas de longitud . Incluso si la palabra de código transmitida es afectada por una ráfaga de longitud , no se verá como otra palabra de código que ha sido afectada por otra ráfaga. Para cada palabra de código, denotemos el conjunto de todas las palabras que difieren de en una ráfaga de longitud Observe que se incluye a sí misma. Por la observación anterior, sabemos que para dos palabras de código diferentes y y son disjuntas. Tenemos palabras de código. Por lo tanto, podemos decir que . Además, tenemos . Al introducir la última desigualdad en la primera, luego tomar el logaritmo base y reorganizar, obtenemos el teorema anterior.
Un resultado más fuerte lo proporciona el límite de Rieger:
Teorema (límite de Rieger) : Si es la capacidad de corrección de errores de ráfaga de un código de bloque lineal, entonces .
Cualquier código lineal que pueda corregir cualquier patrón de ráfaga de longitud no puede tener una ráfaga de longitud como palabra código. Si tuviera una ráfaga de longitud como palabra código, entonces una ráfaga de longitud podría cambiar la palabra código a un patrón de ráfaga de longitud , que también podría obtenerse al hacer un error de ráfaga de longitud en todas las palabras código cero. Si los vectores no son cero en los primeros símbolos, entonces los vectores deben ser de diferentes subconjuntos de una matriz para que su diferencia no sea una palabra código de ráfagas de longitud . Asegurando esta condición, el número de tales subconjuntos es al menos igual al número de vectores. Por lo tanto, el número de subconjuntos sería al menos . Por lo tanto, tenemos al menos símbolos distintos, de lo contrario, la diferencia de dos de tales polinomios sería una palabra código que es una suma de dos ráfagas de longitud Por lo tanto, esto prueba el límite de Rieger.
Definición. Un código de corrección de errores de ráfaga lineal que alcanza el límite de Rieger anterior se denomina código de corrección de errores de ráfaga óptimo.
Límites adicionales para la corrección de errores de ráfaga
Existe más de un límite superior para la tasa de código alcanzable de los códigos de bloque lineales para la corrección de ráfagas múltiples en fase (MPBC). Uno de estos límites está restringido a una longitud máxima de ráfaga cíclica corregible dentro de cada subbloque, o equivalentemente, una restricción sobre la longitud mínima libre de errores o espacio dentro de cada ráfaga en fase. Este límite, cuando se reduce al caso especial de un límite para la corrección de ráfaga única, es el límite de Abramson (un corolario del límite de Hamming para la corrección de errores de ráfaga) cuando la longitud de la ráfaga cíclica es menor que la mitad de la longitud del bloque. [3]
Teorema (número de ráfagas) — Para un alfabeto binario, hay vectores de longitud que son ráfagas de longitud . [1]
Dado que la longitud de la ráfaga es, existe una descripción de ráfaga única asociada con la ráfaga. La ráfaga puede comenzar en cualquiera de las posiciones del patrón. Cada patrón comienza con y contiene una longitud de . Podemos pensar en él como el conjunto de todas las cadenas que comienzan con y tienen una longitud . Por lo tanto, hay un total de posibles patrones de este tipo y un total de ráfagas de longitud. Si incluimos la ráfaga de todos ceros, tenemos vectores que representan ráfagas de longitud
Teorema (Límite en el número de palabras de código) : Si un código de corrección de errores de ráfaga binaria tiene como máximo palabras de código.
Como sabemos que hay ráfagas de longitud . Digamos que el código tiene palabras de código, entonces hay palabras de código que difieren de una palabra de código por una ráfaga de longitud . Cada una de las palabras debe ser distinta, de lo contrario el código tendría una distancia . Por lo tanto, implica
Teorema (límites de Abramson) : Si es un código de corrección de errores de ráfaga lineal binaria , su longitud de bloque debe satisfacer:
Para un código lineal , existen palabras clave. Por nuestro resultado anterior, sabemos que Aislando , obtenemos . Como y deben ser un entero, tenemos .
Observación. se llama redundancia del código y en una formulación alternativa para los límites de Abramson es
Códigos contra incendios
Fuentes: [3] [4] [5]
Si bien los códigos cíclicos en general son herramientas poderosas para detectar errores de ráfaga, ahora consideraremos una familia de códigos cíclicos binarios llamados Códigos de Fuego, que poseen buenas capacidades de corrección de errores de ráfaga única. Por ráfaga única, digamos de longitud , queremos decir que todos los errores que posee una palabra de código recibida se encuentran dentro de un intervalo fijo de dígitos.
Sea un polinomio irreducible de grado sobre , y sea el período de . El período de , y de hecho de cualquier polinomio, se define como el menor entero positivo tal que Sea un entero positivo que satisface y no es divisible por , donde y son el grado y el período de , respectivamente. Defina el Código contra incendios mediante el siguiente polinomio generador :
Demostraremos que es un código de corrección de ráfagas de errores.
Lema 1 —
Sea el máximo común divisor de los dos polinomios. Puesto que es irreducible, o . Supongamos entonces para alguna constante . Pero, es un divisor de puesto que es un divisor de . Pero esto contradice nuestra suposición de que no divide Por lo tanto, se demuestra el lema.
Lema 2 — Si es un polinomio de período , entonces si y sólo si
Si , entonces . Por lo tanto,
Supongamos ahora . Entonces, . Demostramos que es divisible por por inducción sobre . Se deduce el caso base . Por lo tanto, supongamos que . Sabemos que divide a ambos (ya que tiene período ) Pero es irreducible, por lo tanto, debe dividir a ambos y ; por lo tanto, también divide la diferencia de los dos últimos polinomios, . Entonces, se deduce que divide a . Finalmente, también divide: . Por la hipótesis de inducción, , entonces .
Un corolario del Lema 2 es que como tiene período , entonces divide si y sólo si .
Teorema : El Código contra incendios corrige errores de ráfaga [4] [5]
Si podemos demostrar que todas las ráfagas de longitud o menos ocurren en diferentes clases laterales , podemos usarlas como líderes de clases laterales que forman patrones de error corregibles. La razón es simple: sabemos que cada clase lateral tiene una decodificación de síndrome única asociada con ella, y si todas las ráfagas de diferentes longitudes ocurren en diferentes clases laterales, entonces todas tienen síndromes únicos, lo que facilita la corrección de errores.
Prueba del teorema
Sean y polinomios con grados y , que representan ráfagas de longitud y respectivamente con Los números enteros representan las posiciones iniciales de las ráfagas, y son menores que la longitud del bloque del código. Por razones de contradicción, supongamos que y están en la misma clase lateral. Entonces, es una palabra de código válida (ya que ambos términos están en la misma clase lateral). Sin pérdida de generalidad, elija . Por el teorema de la división podemos escribir: para números enteros y . Reescribimos el polinomio de la siguiente manera:
Observe que en la segunda manipulación, introdujimos el término . Se nos permite hacerlo, ya que los Códigos de Incendios operan en . Según nuestra suposición, es una palabra de código válida y, por lo tanto, debe ser un múltiplo de . Como se mencionó anteriormente, dado que los factores de son primos relativos, tiene que ser divisible por . Si observamos de cerca la última expresión derivada para , notamos que es divisible por (por el corolario del Lema 2). Por lo tanto, es divisible por o es . Aplicando nuevamente el teorema de la división, vemos que existe un polinomio con grado tal que:
Entonces podemos escribir:
Igualando el grado de ambos lados, obtenemos Como podemos concluir que implica y . Observe que en la expansión: El término aparece, pero como , la expresión resultante no contiene , por lo tanto y posteriormente Esto requiere que , y . Podemos revisar aún más nuestra división de por para reflejar que es . Sustituyendo nuevamente en obtenemos,
Como , tenemos . Pero es irreducible, por lo tanto y deben ser primos entre sí. Como es una palabra de código, debe ser divisible por , ya que no puede ser divisible por . Por lo tanto, debe ser un múltiplo de . Pero también debe ser un múltiplo de , lo que implica que debe ser un múltiplo de pero esa es precisamente la longitud del bloque del código. Por lo tanto, no puede ser un múltiplo de ya que ambos son menores que . Por lo tanto, nuestra suposición de que es una palabra de código es incorrecta y, por lo tanto , y están en diferentes clases laterales, con síndromes únicos y, por lo tanto, corregibles.
Ejemplo: código de incendio con corrección de error de 5 ráfagas
Con la teoría presentada en la sección anterior, considere la construcción de un código de incendios que corrija errores de ráfaga. Recuerde que para construir un código de incendios, necesitamos un polinomio irreducible , un entero , que represente la capacidad de corrección de errores de ráfaga de nuestro código, y necesitamos satisfacer la propiedad de que no es divisible por el período de . Con estos requisitos en mente, considere el polinomio irreducible , y sea . Como es un polinomio primitivo, su período es . Confirmamos que no es divisible por . Por lo tanto, es un generador de código de incendios. Podemos calcular la longitud de bloque del código evaluando el mínimo común múltiplo de y . En otras palabras, . Por lo tanto, el código de incendios anterior es un código cíclico capaz de corregir cualquier ráfaga de longitud o menos.
Códigos binarios Reed-Solomon
Ciertas familias de códigos, como Reed–Solomon , operan en tamaños de alfabeto mayores que el binario. Esta propiedad otorga a estos códigos potentes capacidades de corrección de errores en ráfagas. Consideremos un código que opera en . Cada símbolo del alfabeto puede representarse mediante bits. Si es un código Reed–Solomon sobre , podemos pensar en un código sobre .
La razón por la que estos códigos son eficaces para la corrección de errores en ráfagas es que cada símbolo está representado por bits y, en general, es irrelevante cuántos de esos bits son erróneos; ya sea que un solo bit o todos los bits contengan errores, desde una perspectiva de decodificación sigue siendo un error de un solo símbolo. En otras palabras, dado que los errores en ráfagas tienden a ocurrir en grupos, existe una gran posibilidad de que varios errores binarios contribuyan a un solo error de símbolo.
Tenga en cuenta que una ráfaga de errores puede afectar a la mayoría de los símbolos, y una ráfaga de puede afectar a la mayoría de los símbolos. Luego, una ráfaga de puede afectar a la mayoría de los símbolos; esto implica que un código de corrección de errores de símbolos puede corregir una ráfaga de longitud como máximo .
En general, un código Reed–Solomon corrector de errores puede corregir cualquier combinación de o menos ráfagas de longitud , además de poder corregir errores aleatorios en el peor de los casos.
Un ejemplo de un código binario RS
Sea un código RS sobre . Este código fue empleado por la NASA en su nave espacial Cassini-Huygens . [6] Es capaz de corregir errores de símbolos. Ahora construimos un código RS binario a partir de . Cada símbolo se escribirá utilizando bits. Por lo tanto, el código RS binario tendrá como parámetros . Es capaz de corregir cualquier ráfaga individual de longitud .
Códigos entrelazados
El entrelazado se utiliza para convertir códigos convolucionales de correctores de errores aleatorios a correctores de errores en ráfagas. La idea básica detrás del uso de códigos entrelazados es mezclar símbolos en el transmisor. Esto conduce a la aleatorización de ráfagas de errores recibidos que están ubicados cerca y luego podemos aplicar el análisis para un canal aleatorio. Por lo tanto, la función principal realizada por el entrelazador en el transmisor es alterar la secuencia de símbolos de entrada. En el receptor, el desentrelazador alterará la secuencia recibida para recuperar la secuencia original inalterada en el transmisor.
Capacidad de corrección de errores de ráfaga del intercalador

Teorema : Si la capacidad de corrección de errores de ráfaga de algún código es entonces la capacidad de corrección de errores de ráfaga de su entrelazado de vías es
Supongamos que tenemos un código que puede corregir todas las ráfagas de longitud El entrelazado puede proporcionarnos un código que puede corregir todas las ráfagas de longitud para cualquier . Si queremos codificar un mensaje de una longitud arbitraria mediante entrelazado, primero lo dividimos en bloques de longitud . Escribimos las entradas de cada bloque en una matriz usando el orden principal de filas. Luego, codificamos cada fila usando el código. Lo que obtendremos es una matriz. Ahora, esta matriz se lee y se transmite en orden principal de columnas. El truco es que si ocurre una ráfaga de longitud en la palabra transmitida, entonces cada fila contendrá aproximadamente errores consecutivos (Más específicamente, cada fila contendrá una ráfaga de longitud al menos y como máximo ). Si entonces y el código puede corregir cada fila. Por lo tanto, el código entrelazado puede corregir la ráfaga de longitud . Por el contrario, si entonces al menos una fila contendrá más de errores consecutivos, y el código podría fallar al corregirlos. Por lo tanto, la capacidad de corrección de errores del código entrelazado es exactamente la misma que la del código original. Esto es así porque:
Intercalador de bloques
La siguiente figura muestra un intercalador de 4 x 3.

El entrelazador anterior se denomina entrelazador de bloques . En este caso, los símbolos de entrada se escriben secuencialmente en las filas y los símbolos de salida se obtienen leyendo las columnas secuencialmente. Por lo tanto, tiene la forma de una matriz. Generalmente, es la longitud de la palabra de código.
Capacidad del intercalador de bloques : para un intercalador de bloques y una ráfaga de longitud, el límite superior de la cantidad de errores es Esto es obvio por el hecho de que estamos leyendo la salida columna por columna y la cantidad de filas es . Según el teorema anterior, la capacidad de corrección de errores hasta la longitud de ráfaga máxima permitida es Para una longitud de ráfaga de , el decodificador puede fallar.
Eficiencia del entrelazador de bloques ( ): se obtiene tomando la relación entre la longitud de ráfaga en la que el decodificador puede fallar y la memoria del entrelazador. Por lo tanto, podemos formular como
Desventajas del entrelazador de bloques: Como se desprende de la figura, las columnas se leen secuencialmente, el receptor puede interpretar una sola fila solo después de recibir el mensaje completo y no antes. Además, el receptor requiere una cantidad considerable de memoria para almacenar los símbolos recibidos y tiene que almacenar el mensaje completo. Por lo tanto, estos factores dan lugar a dos inconvenientes, uno es la latencia y otro es el almacenamiento (cantidad bastante grande de memoria). Estos inconvenientes se pueden evitar utilizando el entrelazador convolucional descrito a continuación.
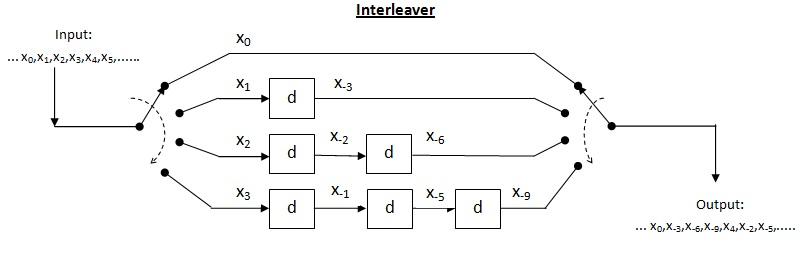
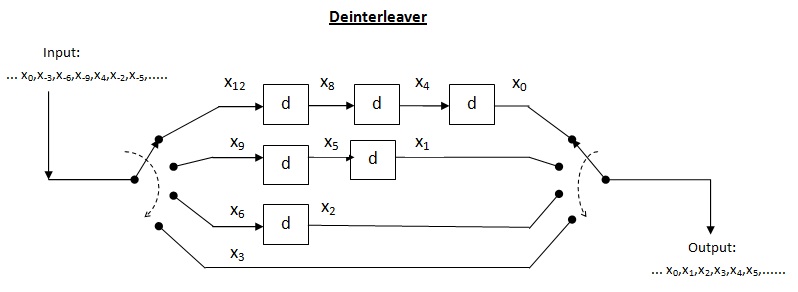
Entrelazador convolucional
El entrelazador cruzado es un tipo de sistema multiplexor-demultiplexor. En este sistema, se utilizan líneas de retardo para aumentar progresivamente la longitud. La línea de retardo es básicamente un circuito electrónico utilizado para retrasar la señal durante un tiempo determinado. Sea el número de líneas de retardo y sea el número de símbolos introducidos por cada línea de retardo. Por lo tanto, la separación entre entradas consecutivas = símbolos. Sea la longitud de la palabra de código Por lo tanto, cada símbolo en la palabra de código de entrada estará en una línea de retardo distinta. Sea que se produzca un error de ráfaga de longitud. Dado que la separación entre símbolos consecutivos es el número de errores que puede contener la salida desentrelazada es Por el teorema anterior, para una capacidad de corrección de errores de hasta , la longitud de ráfaga máxima permitida es Para la longitud de ráfaga del decodificador puede fallar.
Eficiencia del entrelazador cruzado ( ): se obtiene tomando la relación entre la longitud de ráfaga en la que el decodificador puede fallar y la memoria del entrelazador. En este caso, la memoria del entrelazador se puede calcular como
Así, podemos formular lo siguiente:
Rendimiento del entrelazador cruzado: como se muestra en la figura del entrelazador anterior, la salida no es más que los símbolos diagonales generados al final de cada línea de retardo. En este caso, cuando la conmutación del multiplexor de entrada completa aproximadamente la mitad de la conmutación, podemos leer la primera fila en el receptor. Por lo tanto, necesitamos almacenar un máximo de aproximadamente la mitad del mensaje en el receptor para leer la primera fila. Esto reduce drásticamente el requisito de almacenamiento a la mitad. Dado que ahora solo se requiere la mitad del mensaje para leer la primera fila, la latencia también se reduce a la mitad, lo que es una buena mejora con respecto al entrelazador de bloques. Por lo tanto, la memoria total del entrelazador se divide entre el transmisor y el receptor.
Aplicaciones
Disco compacto
Sin códigos de corrección de errores, el audio digital no sería técnicamente factible. [7] Los códigos Reed-Solomon pueden corregir un símbolo corrupto con un solo error de bit con la misma facilidad con la que pueden corregir un símbolo con todos los bits erróneos. Esto hace que los códigos RS sean particularmente adecuados para corregir errores de ráfaga. [5] La aplicación más común de los códigos RS es, con diferencia, en los discos compactos. Además de la corrección de errores básica que proporcionan los códigos RS, un entrelazador cruzado proporciona protección contra los errores de ráfaga debidos a arañazos en el disco. [3]
El actual sistema de audio digital de discos compactos fue desarrollado por NV Philips de los Países Bajos y Sony Corporation de Japón (acuerdo firmado en 1979).
Un disco compacto consta de un disco aluminizado de 120 mm recubierto con una capa de plástico transparente, con una pista en espiral, de aproximadamente 5 km de longitud, que se escanea ópticamente mediante un láser de longitud de onda de ~0,8 μm, a una velocidad constante de ~1,25 m/s. Para lograr esta velocidad constante, la rotación del disco varía de ~8 rev/s mientras se escanea en la parte interior de la pista a ~3,5 rev/s en la parte exterior. Los hoyos y las mesetas son las depresiones (0,12 μm de profundidad) y los segmentos planos que constituyen los datos binarios a lo largo de la pista (0,6 μm de ancho). [8]
El proceso de CD se puede abstraer como una secuencia de los siguientes subprocesos:
- Codificación de canales de origen de señales
- Subprocesos mecánicos de preparación de un disco maestro, producción de discos de usuario y detección de las señales integradas en los discos de usuario durante la reproducción: el canal
- Descodificación de las señales detectadas desde los discos del usuario
El proceso está sujeto tanto a errores de ráfaga como a errores aleatorios. [7] Los errores de ráfaga incluyen aquellos debidos al material del disco (defectos de la película reflectante de aluminio, bajo índice de reflexión del material transparente del disco), la producción del disco (fallas durante la formación del disco y el corte del disco, etc.), la manipulación del disco (rayones, generalmente finos, radiales y ortogonales a la dirección de grabación) y variaciones en el mecanismo de reproducción. Los errores aleatorios incluyen aquellos debidos a la vibración de la onda de señal reconstruida y la interferencia en la señal. CIRC ( código Reed-Solomon entrelazado cruzado ) es la base para la detección y corrección de errores en el proceso de CD. Corrige ráfagas de errores de hasta 3500 bits en secuencia (2,4 mm de longitud como se ve en la superficie del CD) y compensa ráfagas de errores de hasta 12 000 bits (8,5 mm) que pueden ser causadas por pequeños arañazos.
Codificación: Las ondas sonoras se muestrean y se convierten a formato digital mediante un convertidor A/D. La onda sonora se muestrea para determinar su amplitud (a 44,1 kHz o 44 100 pares, uno para cada canal izquierdo y derecho del sonido estéreo). A la amplitud en una instancia se le asigna una cadena binaria de longitud 16. Por lo tanto, cada muestra produce dos vectores binarios de 4 bytes de datos. Cada segundo de sonido grabado da como resultado 44 100 × 32 = 1 411 200 bits (176 400 bytes) de datos. [5] El flujo de datos muestreado de 1,41 Mbit/s pasa por el sistema de corrección de errores y finalmente se convierte en un flujo de 1,88 Mbit/s.
La entrada para el codificador consta de cuadros de entrada, cada uno de los cuales contiene 24 símbolos de 8 bits (12 muestras de 16 bits del conversor A/D, 6 de cada una de las fuentes de datos (sonido) izquierda y derecha). Un cuadro se puede representar mediante donde y son bytes de los canales izquierdo y derecho de la muestra del cuadro.
Inicialmente, los bytes se permutan para formar nuevos cuadros representados por donde representan las muestras izquierda y derecha del cuadro después de 2 cuadros intermedios.
A continuación, estos 24 símbolos de mensaje se codifican utilizando el código C2 (28,24,5) Reed–Solomon, que es un código RS acortado sobre . Este es un corrector de dos errores, siendo de una distancia mínima de 5. Esto agrega 4 bytes de redundancia, formando un nuevo marco: . La palabra de código resultante de 28 símbolos se pasa a través de un entrelazador cruzado (28.4) que conduce a 28 símbolos entrelazados. Estos luego se pasan a través del código RS C1 (32,28,5), lo que da como resultado palabras de código de 32 símbolos de salida codificados. Se realiza una reagrupación adicional de los símbolos impares de una palabra de código con símbolos pares de la siguiente palabra de código para romper cualquier ráfaga corta que aún pueda estar presente después del entrelazado de retardo de 4 cuadros anterior. Por lo tanto, por cada 24 símbolos de entrada habrá 32 símbolos de salida que dan . Finalmente, se agrega un byte de información de control y visualización. [5] Cada uno de los 33 bytes se convierte entonces en 17 bits mediante EFM (modulación de ocho a catorce) y la adición de 3 bits de fusión. Por lo tanto, la trama de seis muestras da como resultado 33 bytes × 17 bits (561 bits) a los que se suman 24 bits de sincronización y 3 bits de fusión, lo que da un total de 588 bits.
Decodificación: El reproductor de CD (decodificador CIRC) recibe el flujo de datos de 32 símbolos de salida. Este flujo pasa primero por el decodificador D1. Depende de los diseñadores individuales de sistemas de CD decidir sobre los métodos de decodificación y optimizar el rendimiento de sus productos. Al estar a una distancia mínima de 5 Los decodificadores D1, D2 pueden corregir cada uno una combinación de errores y borrados de manera que . [5] En la mayoría de las soluciones de decodificación, D1 está diseñado para corregir un solo error. Y en caso de más de 1 error, este decodificador genera 28 borrados. El desentrelazador en la etapa siguiente distribuye estos borrados en 28 palabras de código D2. Nuevamente, en la mayoría de las soluciones, D2 está configurado para tratar solo los borrados (una solución más simple y menos costosa). Si se encontraran más de 4 borrados, D2 genera 24 borrados. Posteriormente, un sistema de ocultación de errores intenta interpolar (a partir de símbolos vecinos) en caso de símbolos incorregibles; en caso contrario, los sonidos correspondientes a dichos símbolos erróneos se silencian.
Rendimiento de CIRC: [7] CIRC oculta errores de busto largo mediante interpolación lineal simple. 2,5 mm de longitud de pista (4000 bits) es la longitud máxima de ráfaga completamente corregible. 7,7 mm de longitud de pista (12 300 bits) es la longitud máxima de ráfaga que se puede interpolar. La tasa de interpolación de muestras es una cada 10 horas a una tasa de error de bit (BER) y 1000 muestras por minuto a BER = Muestras de error indetectables (clics): menos de una cada 750 horas a BER = e insignificante a BER = .
Véase también
- Detección y corrección de errores
- Códigos de corrección de errores con retroalimentación
- Tasa de código
- Corrección de errores de Reed-Solomon
Referencias
- ^ abcd Fong, WH (2011). "Límites de codificación para códigos de corrección de ráfagas múltiples en fase y de ráfaga única". arXiv : 1104.1408 [cs.IT].
- ^ McEliece, RJ (2004). La teoría de la información y la codificación (edición de estudiantes). Cambridge University Press. ISBN 978-0-521-83185-7.
- ^ abc Ling, San; Xing, Chaoping (2004). Teoría de la codificación: un primer curso. Cambridge University Press. ISBN 978-0-521-52923-5.
- ^ ab Moon, Todd K. (2005). Codificación de corrección de errores: métodos y algoritmos matemáticos. Wiley. ISBN 978-0-471-64800-0.
- ^ abcdef Lin, Shu; Costello, Daniel J. (2004). Codificación de control de errores: fundamentos y aplicaciones (2.ª ed.). Pearson-Prentice Hall. ISBN 978-0-13-017973-9.
- ^ "Cassini: ¿Qué tipo de corrección de errores?". quest.arc.nasa.gov . 1999. Archivado desde el original el 27 de junio de 2012.
- ^ Códigos de control de errores algebraicos abc (otoño de 2012): material de apoyo de la Universidad de Stanford
- ^ McEliece, Robert J. (1977). La teoría de la información y la codificación: un marco matemático para la comunicación . Programa de libro avanzado. Addison-Wesley.













































































































































































































![{\displaystyle [mn,mk]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/479cc66e2a601a8f28c80c0d3136e9d45f84728d)










![{\estilo de visualización [255,223,33]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc05fee57b496252bf9064f1e35606fae8d805dc)




![{\displaystyle [2040,1784,33]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0de5be730230c649eac90e01bb084dbcd81319a)




















































