Astrosismología

La astrosismología es el estudio de las oscilaciones en las estrellas. Las estrellas tienen muchos modos y frecuencias de resonancia , y la trayectoria de las ondas sonoras que pasan a través de una estrella depende de la velocidad local del sonido , que a su vez depende de la temperatura local y la composición química. Debido a que los modos de oscilación resultantes son sensibles a diferentes partes de la estrella, informan a los astrónomos sobre la estructura interna de la estrella, lo que de otro modo no sería posible deducir directamente a partir de propiedades generales como el brillo y la temperatura de la superficie.
La astrosismología está estrechamente relacionada con la heliosismología , el estudio de la pulsación estelar específicamente en el Sol . Aunque ambas se basan en la misma física subyacente, hay más información disponible y cualitativamente diferente para el Sol porque su superficie se puede resolver.
Fundamento teórico

Al perturbar linealmente las ecuaciones que definen el equilibrio mecánico de una estrella (es decir, la conservación de la masa y el equilibrio hidrostático ) y suponiendo que las perturbaciones son adiabáticas, se puede derivar un sistema de cuatro ecuaciones diferenciales cuyas soluciones dan la frecuencia y la estructura de los modos de oscilación de una estrella. Generalmente se supone que la estructura estelar es esféricamente simétrica, por lo que el componente horizontal (es decir, no radial) de las oscilaciones se describe mediante armónicos esféricos , indexados por un grado angular y un orden azimutal . En estrellas que no giran, los modos con el mismo grado angular deben tener todos la misma frecuencia porque no hay un eje preferido. El grado angular indica el número de líneas nodales en la superficie estelar, por lo que para valores grandes de , los sectores opuestos se cancelan aproximadamente, lo que dificulta la detección de variaciones de luz. Como consecuencia, los modos solo se pueden detectar hasta un grado angular de aproximadamente 3 en intensidad y aproximadamente 4 si se observan en velocidad radial.
Suponiendo además que la perturbación del potencial gravitatorio es despreciable (la aproximación de Cowling ) y que la estructura de la estrella varía más lentamente con el radio que el modo de oscilación, las ecuaciones se pueden reducir aproximadamente a una ecuación de segundo orden para el componente radial de la función propia de desplazamiento , donde es la coordenada radial en la estrella, es la frecuencia angular del modo de oscilación, es la velocidad del sonido dentro de la estrella, es la frecuencia de Brunt–Väisälä o flotabilidad y es la frecuencia de Lamb. Las dos últimas se definen por y respectivamente. Por analogía con el comportamiento de los osciladores armónicos simples, esto implica que existen soluciones oscilantes cuando la frecuencia es mayor o menor que ambos y . Identificamos el primer caso como modos de presión de alta frecuencia (modos p) y el último como modos de gravedad de baja frecuencia (modos g).
Esta separación básica nos permite determinar (con una precisión razonable) dónde esperamos que resuene qué tipo de modo en una estrella. Al trazar las curvas y (para ), esperamos que los modos p resuenen a frecuencias por debajo de ambas curvas o frecuencias por encima de ambas curvas.
Mecanismos de excitación
Mecanismo kappa
En condiciones bastante específicas, algunas estrellas tienen regiones donde el calor es transportado por la radiación y la opacidad es una función decreciente de la temperatura. Esta protuberancia de opacidad puede impulsar oscilaciones a través del mecanismo (o válvula de Eddington ). Supongamos que, al comienzo de un ciclo de oscilación, la envoltura estelar se ha contraído. Al expandirse y enfriarse ligeramente, la capa en la protuberancia de opacidad se vuelve más opaca, absorbe más radiación y se calienta. Este calentamiento causa expansión, mayor enfriamiento y la capa se vuelve aún más opaca. Esto continúa hasta que la opacidad del material deja de aumentar tan rápidamente, momento en el que la radiación atrapada en la capa puede escapar. La estrella se contrae y el ciclo se prepara para comenzar de nuevo. En este sentido, la opacidad actúa como una válvula que atrapa el calor en la envoltura de la estrella.
Las pulsaciones impulsadas por el mecanismo son coherentes y tienen amplitudes relativamente grandes. Impulsa las pulsaciones en muchas de las estrellas variables más antiguas conocidas, incluidas las variables Cefeidas y RR Lyrae .
Convección superficial
En las estrellas con zonas de convección superficial, los movimientos de fluidos turbulentos cerca de la superficie simultáneamente excitan y amortiguan oscilaciones en un amplio rango de frecuencias. [2] [3] Debido a que los modos son intrínsecamente estables, tienen amplitudes bajas y una vida relativamente corta. Este es el mecanismo impulsor de todos los osciladores de tipo solar.
Bloqueo convectivo
Si la base de una zona de convección superficial es nítida y las escalas de tiempo convectivas son más lentas que las escalas de tiempo de pulsación, los flujos convectivos reaccionan demasiado lentamente a las perturbaciones que pueden acumularse en pulsaciones grandes y coherentes. Este mecanismo se conoce como bloqueo convectivo [4] y se cree que impulsa las pulsaciones en las variables Doradus. [5]
Excitación de marea
Las observaciones del satélite Kepler revelaron sistemas binarios excéntricos en los que las oscilaciones se excitan durante el acercamiento más cercano. [6] Estos sistemas se conocen como estrellas de latido debido a la forma característica de las curvas de luz.
Tipos de osciladores
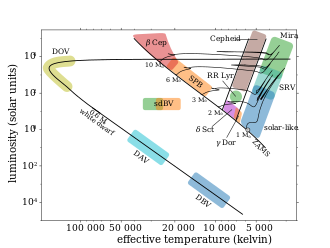
Osciladores similares a los solares
Como las oscilaciones solares son impulsadas por la convección cercana a la superficie, cualquier oscilación estelar causada de manera similar se conoce como oscilaciones similares a las del Sol y las estrellas mismas como osciladores similares a las del Sol . Sin embargo, las oscilaciones similares a las del Sol también ocurren en estrellas evolucionadas (subgigantes y gigantes rojas), que tienen envolturas convectivas, aunque las estrellas no sean similares al Sol .
Variables cefeidas
Las variables cefeidas son una de las clases más importantes de estrellas pulsantes. Son estrellas que queman helio en su núcleo y cuya masa supera las 5 masas solares. Oscilan principalmente en sus modos fundamentales, con períodos típicos que van desde días hasta meses. Sus períodos de pulsación están estrechamente relacionados con sus luminosidades, por lo que es posible determinar la distancia a una cefeida midiendo su período de oscilación, calculando su luminosidad y comparándola con su brillo observado.
Las pulsaciones cefeidas son excitadas por el mecanismo kappa que actúa sobre la segunda zona de ionización del helio.
Variables de RR Lyrae
Las RR Lyraes son similares a las variables Cefeidas pero de menor metalicidad (es decir, Población II ) y masas mucho menores (alrededor de 0,6 a 0,8 veces la solar). Son gigantes que queman helio en su núcleo y oscilan en uno o ambos de sus modos fundamentales o primer sobretono. La oscilación también está impulsada por el mecanismo kappa que actúa a través de la segunda ionización del helio. Muchas RR Lyraes, incluida la propia RR Lyrae, muestran modulaciones de amplitud de período largo, conocidas como el efecto Blazhko .
Estrellas Delta Scuti y Gamma Doradus
Las variables Delta Scuti se encuentran aproximadamente en el punto donde la franja de inestabilidad clásica se cruza con la secuencia principal. Por lo general, son enanas y subgigantes de tipo A a F temprano y los modos de oscilación son modos de presión radial y no radial de orden bajo, con períodos que van de 0,25 a 8 horas y variaciones de magnitud en cualquier punto intermedio. [ aclaración necesaria ] Al igual que las variables Cefeidas, las oscilaciones son impulsadas por el mecanismo kappa que actúa sobre la segunda ionización del helio.
Las variables SX Phoenicis se consideran parientes pobres en metales de las variables Delta Scuti.
Las variables Gamma Doradus se producen en estrellas similares al extremo rojo de las variables Delta Scuti, generalmente de tipo F temprano. Las estrellas muestran múltiples frecuencias de oscilación de entre aproximadamente 0,5 y 3 días, lo que es mucho más lento que los modos de presión de orden bajo. En general, se cree que las oscilaciones de Gamma Doradus son modos de gravedad de orden alto, excitados por bloqueo convectivo.
Siguiendo los resultados de Kepler , parece que muchas estrellas Delta Scuti también muestran oscilaciones Gamma Doradus y, por lo tanto, son híbridas. [7] [8]
Estrellas Ap de oscilación rápida (roAp)
Las estrellas Ap de rápida oscilación tienen parámetros similares a las variables Delta Scuti, siendo en su mayoría de tipo A y F, pero también son fuertemente magnéticas y químicamente peculiares (de ahí el subtipo espectral p ). Sus espectros de modos densos se entienden en términos del modelo de pulsador oblicuo : las frecuencias del modo están moduladas por el campo magnético, que no está necesariamente alineado con la rotación de la estrella (como es el caso en la Tierra). Los modos de oscilación tienen frecuencias de alrededor de 1500 μHz y amplitudes de unos pocos mmag.
Estrellas B de pulsación lenta y variables Beta Cephei
Las estrellas de tipo B de pulsación lenta (SPB) son estrellas de tipo B con períodos de oscilación de unos pocos días, que se entiende que son modos de gravedad de orden superior excitados por el mecanismo kappa. Las variables Beta Cephei son ligeramente más calientes (y por lo tanto más masivas), también tienen modos excitados por el mecanismo kappa y, además, oscilan en modos de gravedad de orden bajo con períodos de varias horas. Ambas clases de osciladores contienen solo estrellas de rotación lenta.
Estrellas subenanas variables de tipo B
Las estrellas subenanas B (sdB) son, en esencia, los núcleos de gigantes que queman helio en el núcleo y que, de algún modo, han perdido la mayor parte de sus envolturas de hidrógeno, hasta el punto de que no existe una capa que queme hidrógeno. Tienen múltiples períodos de oscilación que varían entre aproximadamente 1 y 10 minutos y amplitudes que oscilan entre 0,001 y 0,3 mag en luz visible. Las oscilaciones son modos de presión de orden bajo, excitados por el mecanismo kappa que actúa sobre la protuberancia de opacidad del hierro.
Enanas blancas
Las enanas blancas se caracterizan por su tipo espectral, al igual que las estrellas ordinarias, excepto que la relación entre el tipo espectral y la temperatura efectiva no se corresponde de la misma manera. Por lo tanto, las enanas blancas se conocen por los tipos DO, DA y DB. Los tipos más fríos son físicamente posibles, pero el Universo es demasiado joven para que se hayan enfriado lo suficiente. Se ha descubierto que las enanas blancas de los tres tipos pulsan. Las pulsantes se conocen como estrellas GW Virginis (variables DO, a veces también conocidas como estrellas PG 1159), estrellas V777 Herculis (variables DB) y estrellas ZZ Ceti (variables DA). Todas pulsan en modos g de bajo grado y alto orden. Los períodos de oscilación disminuyen ampliamente con la temperatura efectiva, oscilando entre unos 30 minutos y aproximadamente 1 minuto. Se cree que las estrellas GW Virginis y ZZ Ceti se excitan por el mecanismo kappa; las estrellas V777 Herculis por bloqueo convectivo.
Misiones espaciales
Varias naves espaciales pasadas, presentes y futuras tienen estudios de astrosismología como una parte importante de sus misiones (orden cronológico).
- WIRE – Satélite de la NASA lanzado en 1999. El rastreador de estrellas de dos pulgadas de apertura, un gran telescopio infrarrojo que fracasó, se utilizó durante más de una década como instrumento astrosismológico para detectar estrellas brillantes. Regresó a la atmósfera terrestre en 2011.
- MOST – Satélite canadiense lanzado en 2003. La primera nave espacial dedicada a la astrosismología.
- CoRoT – Un satélite de búsqueda de planetas y astrosismología dirigido por la ESA y lanzado en 2006.
- Telescopio espacial Kepler : una nave espacial de la NASA para la detección de planetas lanzada en 2009 y reutilizada como K2 debido a que la falla de una segunda rueda de reacción impidió que el telescopio continuara monitoreando el mismo campo.
- BRITE – Una constelación de nanosatélites que se utiliza para estudiar las estrellas oscilantes más brillantes. Los dos primeros satélites se lanzaron el 25 de febrero de 2013.
- TESS – Un buscador de planetas de la NASA que estudiará estrellas brillantes en la mayor parte del cielo. Se lanzó en 2018.
- PLATO – Una misión planificada de la ESA que explotará específicamente la astrosismología para obtener masas y radios precisos de planetas en tránsito.
Véase también
- Separación de frecuencia
- Terremoto estelar
- Discosismología : el estudio de los modos de oscilación en los discos de acreción.
- Sismología : estudio científico de los terremotos y la propagación de ondas elásticas a través de un planeta.
- Whole Earth Telescope : colaboración internacional para observar estrellas variables
Referencias
- ^ Christensen-Dalsgaard, J.; Dappen, W.; Ajukov, S.V. y (1996), "El estado actual del modelado solar", Science , 272 (5266): 1286–1292, Bibcode :1996Sci...272.1286C, doi :10.1126/science.272.5266.1286, PMID 8662456, S2CID 35469049
- ^ Goldreich, Peter ; Keeley, Douglas A. (febrero de 1977), "Sismología solar. II - La excitación estocástica de los modos p solares por convección turbulenta", The Astrophysical Journal , 212 : 243–251, Bibcode :1977ApJ...212..243G, doi : 10.1086/155043
- ^ Christensen-Dalsgaard, Jørgen ; Frandsen, Søren (enero de 1983), "Oscilaciones estelares de 5 minutos", Solar Physics , 82 (1–2): 469–486, Bibcode :1983SoPh...82..469C, doi :10.1007/bf00145588, S2CID 125358311
- ^ Pesnell, W. Dean (marzo de 1987), "Un nuevo mecanismo impulsor de las pulsaciones estelares", The Astrophysical Journal , 314 : 598–604, Bibcode :1987ApJ...314..598P, doi :10.1086/165089
- ^ Guzik, Joyce A.; Kaye, Anthony B.; Bradley, Paul A.; Cox, Arthur N.; Neuforge, Corinne (10 de octubre de 2000), "Impulso de las pulsaciones en modo de gravedad en las variables γ Doradus", The Astrophysical Journal Letters , 542 (1): L57–L60, Bibcode :2000ApJ...542L..57G, doi : 10.1086/312908
- ^ Thompson, SE; Everett, M.; Mullally, F.; Barclay, T. y (2012), "Una clase de sistemas binarios excéntricos con distorsiones de marea dinámicas descubiertas con Kepler", The Astrophysical Journal , 753 (1): 86, arXiv : 1203.6115 , Bibcode :2012ApJ...753...86T, doi :10.1088/0004-637x/753/1/86, S2CID 119203028
- ^ Grigahc\'ene, A.; Antoci, V.; Balona, L.; Catanzaro, G. y (2010), "Pulsadores híbridos $\gamma$ Doradus-$\delta$ Scuti: nuevos conocimientos sobre la física de las oscilaciones a partir de las observaciones de Kepler", The Astrophysical Journal Letters , 713 (2): L192 – L197 , arXiv : 1001.0747 , Bibcode :2010ApJ...713L.192G, doi :10.1088/2041-8205/713/2/L192, S2CID 56144432
- ^ Balona, LA (2014), "Bajas frecuencias en las estrellas $\delta$ Scuti de Kepler", Monthly Notices of the Royal Astronomical Society , 437 (2): 1476–1484, Bibcode :2014MNRAS.437.1476B, doi : 10.1093/mnras/stt1981
Lectura adicional
- Aerts, Conny; Christensen-Dalsgaard, Jørgen; Kurtz, Donald (2010). Astrosismología . Biblioteca de Astronomía y Astrofísica. Dordrecht, Nueva York: Springer. ISBN 978-1-4020-5803-5.
- Christensen-Dalsgaard, Jørgen. "Apuntes de conferencias sobre oscilaciones estelares" . Consultado el 5 de junio de 2015 .
- Pijpers, Frank P. (2006). Métodos en heliosismología y astrosismología . Londres: Imperial College Press. ISBN 978-1-8609-4755-1.
Software
El paquete Variable Star (en lenguaje R) proporciona las principales funciones para analizar patrones sobre los modos de oscilación de estrellas variables. También se proporciona una interfaz de usuario para la experimentación con datos sintéticos.














