Asignación de ruta

La asignación de ruta , elección de ruta o asignación de tráfico se refiere a la selección de rutas (alternativamente llamadas caminos) entre orígenes y destinos en redes de transporte . Es el cuarto paso en el modelo de pronóstico de transporte convencional, después de la generación de viajes , la distribución de viajes y la elección del modo . El análisis de intercambio zonal de la distribución de viajes proporciona tablas de viajes de origen-destino. El análisis de elección de modo dice qué viajeros usarán qué modo . Para determinar las necesidades de instalaciones y los costos y beneficios, necesitamos saber el número de viajeros en cada ruta y enlace de la red (una ruta es simplemente una cadena de enlaces entre un origen y un destino). Necesitamos realizar la asignación de tráfico (o viaje). Supongamos que hay una red de autopistas y sistemas de tránsito y una adición propuesta. Primero queremos saber el patrón actual de demora del tráfico y luego qué sucedería si se hiciera la adición.

El Wikilibro Investigación de Operaciones tiene una página sobre el tema: Problema de transporte y asignación

El problema de calcular el número de usuarios de cada ruta existe desde hace mucho tiempo. Los planificadores comenzaron a analizarlo en profundidad cuando se empezaron a desarrollar autopistas y vías rápidas. Las autopistas ofrecían un nivel de servicio superior al sistema de calles locales y desviaban el tráfico del sistema local. Al principio, la técnica era el desvío. Se utilizaban proporciones de tiempo de viaje, atenuadas por consideraciones de costos, comodidad y nivel de servicio .

Los investigadores del Estudio de Transporte del Área de Chicago (CATS) desarrollaron curvas de desviación para autopistas en comparación con calles locales. También se trabajó mucho en California, ya que este estado ya tenía experiencias tempranas en la planificación de autopistas. Además del trabajo de desviación, el CATS abordó algunos problemas técnicos que surgen cuando se trabaja con redes complejas. Uno de los resultados fue el algoritmo Bellman-Ford-Moore para encontrar los caminos más cortos en las redes.

El problema que no se abordó con el método de desvío fue la retroalimentación de la cantidad de tráfico en los enlaces y rutas. Si muchos vehículos intentan utilizar una instalación, esta se congestiona y el tiempo de viaje aumenta. A falta de alguna forma de tener en cuenta la retroalimentación, los primeros estudios de planificación (en realidad, la mayoría en el período 1960-1975) ignoraron la retroalimentación. Utilizaron el algoritmo de Moore para determinar las rutas más cortas y asignaron todo el tráfico a las rutas más cortas. Esto se llama asignación de todo o nada porque todo el tráfico de i a j se mueve a lo largo de una ruta o no lo hace.

La asignación de la ruta más corta o de todo o nada no es trivial desde un punto de vista técnico-computal. Cada zona de tráfico está conectada a n - 1 zonas, por lo que hay numerosos caminos a considerar. Además, en última instancia, nos interesa el tráfico en los enlaces. Un enlace puede ser parte de varias rutas y el tráfico a lo largo de las rutas debe sumar enlace por enlace.

Se puede argumentar a favor de la estrategia del todo o nada. La idea es la siguiente: el estudio de planificación sirve para respaldar las inversiones de modo que se disponga de un buen nivel de servicio en todos los enlaces. Utilizando los tiempos de viaje asociados con el nivel de servicio planificado, los cálculos indican cómo fluirá el tráfico una vez que se implementen las mejoras. Conociendo las cantidades de tráfico en los enlaces, se puede calcular la capacidad que se debe suministrar para cumplir con el nivel de servicio deseado.

Para tener en cuenta el efecto de la carga de tráfico en los tiempos de viaje y los equilibrios de tráfico, se desarrollaron varios procedimientos de cálculo heurístico . Una heurística procede de forma incremental. El tráfico que se va a asignar se divide en partes (normalmente 4). Se asigna la primera parte del tráfico. Se calculan los nuevos tiempos de viaje y se asigna la siguiente parte del tráfico. El último paso se repite hasta que se asigna todo el tráfico. El CATS utilizó una variación de esto; se asignó fila por fila en la tabla OD.

La heurística incluida en la colección de programas informáticos de la FHWA procede de otra manera.

• 0. Comience cargando todo el tráfico utilizando un procedimiento de todo o nada.
• 1. Calcule los tiempos de viaje resultantes y reasigne el tráfico.
• 2. Ahora, comience a reasignar utilizando pesos. Calcule los tiempos de viaje ponderados en las dos cargas anteriores y utilícelos para la próxima asignación. La última iteración obtiene un peso de 0,25 y la anterior, un peso de 0,75.
• 3. Continuar.

Estos procedimientos parecen funcionar "bastante bien", pero no son exactos.

Dafermos (1968) aplicó el algoritmo de Frank-Wolfe (1956, Florian 1976), que puede utilizarse para tratar el problema del equilibrio del tráfico. Supongamos que estamos considerando una red de autopistas. Para cada enlace existe una función que establece la relación entre la resistencia y el volumen de tráfico. La Oficina de Carreteras Públicas (BPR) desarrolló una función de congestión (o volumen-retardo, o rendimiento del enlace) de enlaces (arcos), que denominaremos S _a (v _a )

${\displaystyle S_{a}({v_{a}}\right)=t_{a}({1+0.15\left({\frac {v_{a}}{c_{a}}}\right)^{4}}\right)}$

• t _a = tiempo de recorrido en flujo libre en el enlace a por unidad de tiempo
• v _a = volumen de tráfico en el enlace a por unidad de tiempo (algo más preciso: flujo que intenta utilizar el enlace a ).
• c _a = capacidad del enlace a por unidad de tiempo
• S _a (v _a ) es el tiempo promedio de viaje de un vehículo en el enlace a

Existen otras funciones de congestión. El CATS ha utilizado durante mucho tiempo una función diferente de la que utiliza el BPR, pero parece haber poca diferencia entre los resultados cuando se comparan las funciones del CATS y del BPR.

Para asignar tráfico a rutas y enlaces, tenemos que tener reglas, y existen las conocidas condiciones de equilibrio de Wardrop ^[1] . La esencia de estas es que los viajeros se esforzarán por encontrar la ruta más corta (de menor resistencia) desde el origen hasta el destino, y el equilibrio de la red se produce cuando ningún viajero puede reducir el esfuerzo de viaje cambiando a una nueva ruta. Estas se denominan condiciones óptimas para el usuario, ya que ningún usuario se beneficiará al cambiar las rutas de viaje una vez que el sistema esté en equilibrio.

El equilibrio óptimo del usuario se puede encontrar resolviendo el siguiente problema de programación no lineal

${\displaystyle \min \sum _{a}{\int _{0}^{v_{a}}{S_{a}\left(x\right)}}dx}$

sujeto a:

${\displaystyle v_{a}=\suma _{i}{\suma _{j}{\suma _{r}{\alpha _{ij}^{ar}x_{ij}^{r}}}}}$

${\displaystyle \suma _{r}{x_{ij}^{r}=T_{ij}}}$

${\displaystyle v_{a}\geq 0,\;x_{ij}^{r}\geq 0}$

donde es el número de vehículos en la ruta r desde el origen i hasta el destino j . Por lo tanto, la restricción (2) dice que todo viaje debe realizarse – i = 1 ... n; j = 1 ... n$estilo de visualización x_{ij}^{r}}$

${\displaystyle \alpha _{ij}^{ar}}$= 1 si el enlace a está en la ruta r de i a j; cero en caso contrario. Por lo tanto, la restricción (1) suma el tráfico en cada enlace. Existe una restricción para cada enlace de la red. La restricción (3) asegura que no haya tráfico negativo.

Un ejemplo de Eash, Janson y Boyce (1979) ilustrará la solución del problema del programa no lineal. Hay dos enlaces desde el nodo 1 al nodo 2 y hay una función de resistencia para cada enlace (ver Figura 1). Las áreas bajo las curvas en la Figura 2 corresponden a la integración de 0 a a en la ecuación 1; suman 220.674. Nótese que la función para el enlace b está graficada en la dirección inversa.

${\displaystyle S_{a}=15\left({1+0.15\left({\frac {v_{a}}{1000}}\right)^{4}}\right)}$

${\displaystyle S_{b}=20\left({1+0.15\left({\frac {v_{b}}{3000}}\right)^{4}}\right)}$

${\displaystyle v_{a}+v_{b}=8000}$

Figura 1: Red de dos rutas

Figura 2: Solución gráfica al problema de asignación de equilibrio

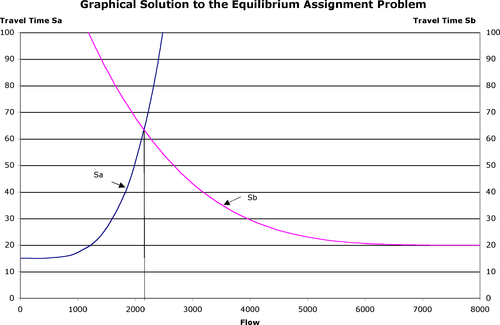
Figura 3: Asignación de vehículos que no satisfacen la condición de equilibrio

En equilibrio hay 2.152 vehículos en el enlace A y 5.847 en el enlace B. El tiempo de viaje es el mismo en cada ruta: aproximadamente 63 minutos.

La figura 3 ilustra una distribución de vehículos que no es coherente con la solución de equilibrio. Las curvas no han cambiado. Pero con la nueva distribución de vehículos por rutas, el área sombreada debe incluirse en la solución, por lo que la solución de la figura 3 es mayor que la solución de la figura 2 por el área del área sombreada.

El modelo de planificación del transporte urbano evolucionó como un conjunto de pasos a seguir, y los modelos evolucionaron para su uso en cada paso. A veces había pasos dentro de los pasos, como fue el caso del primer enunciado del modelo de Lowry . En algunos casos, se ha observado que los pasos pueden integrarse. En términos más generales, los pasos se abstraen de las decisiones que pueden tomarse simultáneamente, y sería deseable replicar mejor eso en el análisis.

Los modelos de demanda desagregada se desarrollaron inicialmente para tratar el problema de elección del modo de transporte. Ese problema supone que uno ha decidido hacer un viaje, adónde irá ese viaje y a qué hora se realizará. Se han utilizado para tratar el contexto más amplio implícito. Por lo general, se desarrollará un modelo anidado, por ejemplo, comenzando con la probabilidad de que se realice un viaje, luego examinando la elección entre lugares y luego la elección del modo de transporte. El momento del viaje es un poco más difícil de tratar.

El modelo de entropía doblemente restringida de Wilson ha sido el punto de partida de los esfuerzos a nivel agregado. Ese modelo contiene la restricción

${\displaystyle t_{ij}c_{ij}=C}$

donde son los costos de viaje del enlace, se refiere al tráfico en un enlace y C es una restricción de recursos que se debe dimensionar al ajustar el modelo con los datos. En lugar de utilizar esa forma de restricción, se puede utilizar la función de resistencia que aumenta monótonamente utilizada en la asignación de tráfico. El resultado determina los movimientos de zona a zona y asigna tráfico a las redes, y eso tiene mucho sentido desde la forma en que uno imaginaría que funciona el sistema: el tráfico de zona a zona depende de la resistencia ocasionada por la congestión.$estilo de visualización c_{ij}}$$estilo de visualización t_{ij}}$

Como alternativa, la función de resistencia del enlace puede incluirse en la función objetivo (y la función de costo total eliminarse de las restricciones).

Se ha desarrollado un enfoque de elección desagregado generalizado, al igual que un enfoque agregado generalizado. La gran pregunta es la de las relaciones entre ellos. Cuando utilizamos un modelo macro, nos gustaría saber el comportamiento desagregado que representa. Si estamos haciendo un análisis micro, nos gustaría saber las implicaciones agregadas del análisis.

Wilson deriva un modelo gravitacional con parámetros ponderados que indican algo sobre el atractivo de los orígenes y destinos. Sin demasiadas matemáticas, podemos escribir enunciados de probabilidad de elección basados ​​en el atractivo, y estos adoptan una forma similar a algunas variedades de modelos de demanda desagregada.

Desde hace mucho tiempo se reconoce que la demanda de viajes está influida por la oferta de la red. El ejemplo de la apertura de un nuevo puente donde antes no había ninguno, que genera tráfico adicional, se conoce desde hace siglos. Se han realizado muchas investigaciones para desarrollar métodos que permitan que el sistema de previsión tenga en cuenta directamente este fenómeno. Evans (1974) publicó una tesis doctoral sobre una combinación matemáticamente rigurosa del modelo de distribución de la gravedad con el modelo de asignación de equilibrio. La primera cita de esta integración es el trabajo de Irwin y Von Cube, tal como lo relatan Florian et al. (1975), quienes comentan el trabajo de Evans:

"El trabajo de Evans se parece un poco a los algoritmos desarrollados por Irwin y Von Cube ['Capacity Restraint in Multi-Travel Mode Assignment Programs' HRB Bulletin 347 (1962)] para un estudio de transporte de Toronto . Su trabajo permite la retroalimentación entre la asignación congestionada y la distribución de viajes, aunque aplican procedimientos secuenciales. Partiendo de una solución inicial del problema de distribución, los viajes interzonales se asignan a las rutas más cortas iniciales. Para iteraciones sucesivas, se calculan nuevas rutas más cortas y sus longitudes se utilizan como tiempos de acceso para la entrada del modelo de distribución. Los nuevos flujos interzonales se asignan luego en cierta proporción a las rutas ya encontradas. El procedimiento se detiene cuando los tiempos interzonales para iteraciones sucesivas son casi iguales".

Florian et al. propusieron un método algo diferente para resolver la asignación de distribución combinada, aplicando directamente el algoritmo de Frank-Wolfe. Boyce et al. (1988) resumen la investigación sobre problemas de equilibrio de redes, incluida la asignación con demanda elástica.

Un problema de tres enlaces no se puede resolver gráficamente, y la mayoría de los problemas de redes de transporte involucran una gran cantidad de nodos y enlaces. Eash et al., por ejemplo, estudiaron la red de carreteras del condado de DuPage, donde había alrededor de 30.000 enlaces de una sola vía y 9.500 nodos. Debido a que los problemas son grandes, se necesita un algoritmo para resolver el problema de asignación, y se utiliza el algoritmo de Frank-Wolfe (con varias modificaciones modernas desde su primera publicación). Comienza con una asignación de todo o nada y luego sigue la regla desarrollada por Frank-Wolfe para iterar hacia el valor mínimo de la función objetivo. (El algoritmo aplica soluciones factibles sucesivas para lograr la convergencia a la solución óptima. Utiliza un procedimiento de búsqueda eficiente para mover el cálculo rápidamente hacia la solución óptima). Los tiempos de viaje corresponden a las variables duales en este problema de programación.

Es interesante que el algoritmo de Frank-Wolfe estuviera disponible en 1956. Su aplicación se desarrolló en 1968, y pasaron casi otras dos décadas antes de que el primer algoritmo de asignación de equilibrio se incorporara a un software de planificación de transporte de uso común (Emme y Emme/2, desarrollado por Florian y otros en Montreal). No queremos sacar ninguna conclusión general de la observación de la lentitud de la aplicación, principalmente porque podemos encontrar ejemplos contrarios sobre el ritmo y el patrón de desarrollo de la técnica. Por ejemplo, el método símplex para la solución de problemas de programación lineal se elaboró ​​y aplicó ampliamente antes del desarrollo de gran parte de la teoría de la programación.

El enunciado del problema y el algoritmo tienen aplicaciones generales en toda la ingeniería civil : hidráulica, estructuras y construcción (véase Hendrickson y Janson, 1984).

Los modelos de asignación de rutas se basan, al menos en cierta medida, en estudios empíricos sobre cómo las personas eligen rutas en una red . Dichos estudios se centran generalmente en un modo en particular y utilizan modelos de preferencia declarada o de preferencia revelada .

Se ha descubierto que los ciclistas prefieren los carriles para bicicletas designados y evitan las colinas empinadas. ^[2]

El transporte público se ha tenido en cuenta desde hace mucho tiempo en el contexto de la asignación de rutas ^[3] y se han realizado muchos estudios sobre la elección de rutas de transporte. Entre otros factores, los usuarios del transporte público intentan minimizar el tiempo total de viaje, el tiempo o la distancia a pie y el número de transbordos. ^[4]

• Elección de ruta (desambiguación)

• Dafermos, Stella. C. y FT Sparrow El problema de asignación de tráfico para una red general". J. of Res. de la Oficina Nacional de Normas, 73B, págs. 91-118. 1969.
• Florian, Michael ed., Métodos de equilibrio de tráfico, Springer-Verlag, 1976.
• Eash, Ronald, Bruce N. Janson y David Boyce, Asignación de viaje de equilibrio: ventajas e implicaciones para la práctica, Transportation Research Record 728, págs. 1–8, 1979.
• Evans, Suzanne P. . "Derivación y análisis de algunos modelos para combinar la distribución y asignación de viajes". Transportation Research, vol. 10, págs. 37-57, 1976
• Hendrickson, CT y BN Janson, "Una formulación de flujo de red común para varios problemas de ingeniería civil", Civil Engineering Systems 1(4), págs. 195-203, 1984