Arco con asa de cesta

Un arco de asa de cesta (también arco deprimido o arco de chuleta [1] ) se caracteriza por un perfil intradós formado por una secuencia de arcos circulares, cada uno tangente a sus vecinos, lo que da como resultado una transición suave entre arcos. La forma más simple, un arco de tres centros, consta de tres segmentos de arco con centros distintos, mientras que un arco de cinco centros también se usa comúnmente. [2] Este tipo de arco prevalece en aplicaciones arquitectónicas, particularmente en la construcción de puentes. La forma de un arco de asa de cesta se asemeja a la de una semielipse [ 3] , presentando una curvatura continua que varía desde las extremidades del eje largo hasta el vértice del eje corto. También se lo conoce como arco deprimido o arco de cesta [4] , lo que resalta su curvatura distintiva y su función estructural. [5]
Historia

Desde la época romana, las bóvedas de los puentes se construyen con arcos de medio punto , formando una media circunferencia completa. A partir de la Alta Edad Media , el arco rebajado , una media circunferencia incompleta, se utilizó para construir bóvedas que tenían una altura inferior a la mitad de su vano. [6]
El arco apuntado , que enfatiza la altura al elevarse por encima de la mitad de la abertura, no se utilizó en la construcción de puentes hasta la Edad Media. [6]
El arco de medio punto apareció a principios del Renacimiento , ofreciendo ventajas estéticas sobre las bóvedas rebajadas, en particular porque sus arcos finales estaban tangenciales verticalmente a los soportes. [6]

Las primeras aplicaciones de los arcos con asas de cesta en Francia se pueden ver en el Pont-Neuf de Toulouse, construido en el siglo XVI, y en el Pont Royal en el siglo siguiente. [7]
En el siglo XVIII, el uso de arcos de medio punto se hizo frecuente, particularmente con tres centros, como lo ejemplifican los puentes de Vizille , Lavaur, Gignac , [8] Blois (1716-1724), Orleans (1750-1760), Moulins (1756-1764) y Saumur (1756-1770). [7]
El notable arquitecto Jean-Rodolphe Perronet diseñó puentes con once centros durante la segunda mitad del siglo XVIII, incluidos los de Mantes (1757-1765), Nogent (1766-1769) y Neuilly (1766-1774). El puente de Tours (1764-1777) también tenía once centros. Otros arcos se redujeron generalmente a un tercio o un poco más, [7] excepto el de Neuilly , que se redujo a un cuarto.
En el siglo XIX, los arcos de medio punto se utilizaron en los primeros grandes puentes ferroviarios de Francia, entre ellos el puente Cinq-Mars (1846-1847), el puente Port-de-Piles (1846-1848), los puentes Morandière: Montlouis (1843-1845) y Plessis-les-Tours (1855-1857).
En Inglaterra, mientras que el Puente de Gloucester (1826-1827) [9] y el Puente de Londres (1824-1831) [10] eran elípticos, el Puente de Waterloo en Londres (1816-1818) mantuvo la forma de arco de asa de canasta. [7]
Se siguieron construyendo varios arcos de asa de cesta hasta finales del siglo XIX y principios del XX. Entre los ejemplos más notables se incluyen el puente de la Avenida Edmonson en Baltimore (1908-1909) con tres centros, [11] el puente Annibal (1868-1870) [12] y el puente del Diablo (1870-1872) [13] con cinco centros, el puente del Emperador Francisco en Praga (1898-1901) con siete centros, [14] y el puente Signac (1871-1872) con diecinueve centros. [15]
En los Estados Unidos, el viaducto Thomas , que presenta un arco en forma de canasta, se construyó entre 1833 y 1835. [16] Ahora es propiedad de CSX Transportation y sigue siendo uno de los puentes ferroviarios más antiguos que aún se encuentran en servicio.
Comparación entre el arco del asa de la cesta y la elipse
Estética
Los arquitectos antiguos daban mucha importancia a los métodos empleados para definir el contorno del arco carpanel. La flexibilidad inherente a estos procesos permitía una amplia variedad de configuraciones, lo que llevó a muchos arquitectos a preferir este tipo de curva frente a la elipse, cuyo contorno está determinado rígidamente por principios geométricos. [17]
En el caso de una elipse, la apertura de la bóveda y la altura en el centro (que corresponde a los ejes mayor y menor) dan como resultado puntos fijos a lo largo de la curva del intradós , sin dejar espacio para modificaciones arquitectónicas. Por el contrario, la curva multicentro ofrece una mayor libertad de diseño, permitiendo a los arquitectos ajustar la base y el vértice de la curva según sus preferencias, dependiendo de la disposición de los centros. Esta adaptabilidad hizo del arco carpanel una opción atractiva para quienes buscaban flexibilidad estética. [17]
Ventajas y desventajas
Las ventajas de este enfoque de diseño fueron significativas: el establecimiento de ranuras a escala real se percibió como más fácil y preciso, lo que permitió el diseño inmediato en el sitio de las normales y las juntas de los segmentos. [18]
El número de formas de dovelas estaba limitado por el número de radios distintos empleados, mientras que para los arcos elípticos, este número era típicamente igual a la mitad del número de dovelas más uno. [18]
Sin embargo, la discontinuidad del trazado dio lugar a la aparición de dovelas antiestéticas, que no siempre pudieron eliminarse durante los trabajos de restauración. [18]
Trazado de curvas con tres centros
El antiguo óvalo
Aunque el arco de asa de cesta no se utilizó para las bóvedas de puentes en la antigüedad, encontró aplicación en la construcción de otros tipos de bóvedas. Herón de Alejandría , autor de tratados matemáticos más de un siglo antes de la era común, describió un método sencillo para trazar este arco. [19]
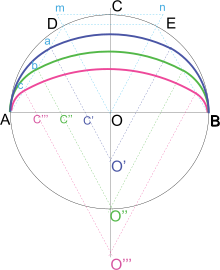
En el método de Heron, si AB representa el ancho de la bóveda prevista y la altura (o elevación) es indeterminada, se describe una media circunferencia sobre AB. Se traza una línea vertical OC a través del punto C sobre este arco, y se construye una tangente mn en el punto C. Las longitudes Cm y Cn se toman como iguales a la mitad del radio del arco. Al conectar los puntos mO y nO, se establecen los puntos D y E. Luego se traza un triángulo isósceles DOE, con su base igual a la altura del arco. A continuación, el segmento de línea DA se divide en cuatro partes iguales, y se trazan paralelas a DO a través de estos puntos de división (a, b, c). Las intersecciones de estas paralelas con el eje horizontal AB y el eje vertical extendido CO producen los centros necesarios para trazar varias curvas con tres centros a lo largo de AB, a menudo denominadas el óvalo antiguo. [19]

A medida que el arco de asa de cesta se hizo más común en la construcción de puentes, surgieron numerosos procedimientos para trazarlo, lo que llevó a un aumento en el número de centros utilizados. [20] El objetivo era crear curvas perfectamente continuas con un contorno estéticamente agradable. Dada la naturaleza indeterminada del problema, a menudo se imponían ciertas condiciones de manera arbitraria para lograr el resultado deseado.
Por ejemplo, a veces se aceptaba que los arcos de círculo que componían la curva debían corresponder a ángulos iguales en el centro, mientras que en otras ocasiones se exigía que estos arcos tuvieran la misma longitud. Además, se permitía que la amplitud de los ángulos o las longitudes de los radios sucesivos variaran según proporciones específicas.
También se estableció una relación constante entre la reducción del arco y el número de centros utilizados para trazar la curva del intradós. Esta reducción se mide por la relación entre la elevación (b) y el ancho del arco (2a), expresada como b/2a. Las relaciones aceptables pueden incluir un tercio, un cuarto o un quinto; sin embargo, si la relación cae por debajo de un quinto, generalmente se prefiere un arco circular en lugar del arco en asa o la elipse. Para pendientes más pronunciadas, es aconsejable emplear al menos cinco centros, y algunos diseños utilizan hasta once centros, como se ve en la curva del puente Neuilly, o incluso hasta diecinueve para el puente Signac. Como uno de los centros siempre debe estar ubicado en el eje vertical, los centros restantes se disponen simétricamente, lo que da como resultado un número total de centros impar.
El método Huygens

Para construir curvas con tres centros, Huyghens describe un método que implica trazar arcos de radios variables correspondientes a ángulos iguales, específicamente ángulos de 60 grados. [21]
Para comenzar, se supone que AB representa la abertura y OE la flecha de la bóveda. Desde el punto central O, se traza un arco AMF utilizando el radio OA. El arco AM se toma entonces como un sexto de la circunferencia, lo que significa que su cuerda es igual al radio OA. Se trazan las cuerdas AM y MF, seguidas de una línea Em que pasa por el punto E, que es el punto final del eje menor, paralela a MF.
La intersección de las cuerdas AM y Em determina el punto m, límite del primer arco. Al trazar la línea mP paralela a MO, se establecen los puntos n y P como los dos centros necesarios para la construcción. El tercer centro n se sitúa a una distancia n'O del eje OE, igual a nO.
El análisis de la figura revela que los tres arcos (Am, mEm' y m'B) componen la curva y corresponden a ángulos iguales en los centros Anm, mPm' y m'n'B, todos de 60 grados. [21]
El método Bossut

Charles Bossut propuso un método más eficiente para trazar una curva de tres centros, que simplifica el proceso.
En este método, AB representa la abertura y OE denota la flecha de la bóveda, que sirven como los ejes largo y corto de la curva. Para comenzar, se dibuja el segmento de línea AE. Desde el punto E, se toma un segmento EF', igual a la diferencia entre OA y OE. Luego se dibuja una línea perpendicular desde el punto medio m de AF'. Los puntos n y P, donde esta perpendicular interseca el eje mayor y la prolongación del eje menor, sirven como los dos centros necesarios para la construcción. [22]
Al utilizar la misma apertura y elevación, la curva producida por este método exhibe una desviación mínima de las generadas por técnicas anteriores.
Curvas con más de tres centros
Para las curvas con más de tres centros, los métodos indicados por Bérard, Jean-Rodolphe Perronet , Émiland Gauthey y otros consistían, como para el puente de Neuilly , en proceder por ensayo y error.
Trazar una primera curva aproximada según datos arbitrarios, cuyos elementos fueron luego rectificados, mediante fórmulas más o menos ciertas, de modo que pasaran exactamente por los extremos de los ejes mayor y menor.
El método Michal

En un artículo publicado en 1831, el matemático Michal abordó el problema de la construcción de curvas con un enfoque científico. Desarrolló tablas que contenían los datos necesarios para dibujar curvas con 5, 7 y 9 centros, logrando resultados precisos sin necesidad de ensayo y error.
El método de cálculo de Michal es aplicable a curvas con cualquier número de centros. Observó que las condiciones necesarias para resolver el problema pueden ser algo arbitrarias. Para abordar esto, propuso que las curvas se construyeran utilizando arcos de un círculo que subtendieran ángulos iguales o arcos de igual longitud. Sin embargo, para determinar completamente los radios de estos arcos, también postuló que los radios deberían corresponder a los radios de curvatura de una elipse centrada en el punto medio de cada arco, donde la abertura sirve como eje mayor y el ascenso funciona como eje menor. [23]
A medida que aumenta el número de centros, la curva resultante se aproxima a la forma de una elipse con la misma apertura y pendiente.
La siguiente tabla ilustra la construcción de un arco carpanel, caracterizado por ángulos iguales subtendidos por los distintos arcos que lo componen. Los valores proporcionales para los radios iniciales se calculan utilizando como unidad de medida la mitad del vano. Además, el voladizo se define como la relación entre la flecha (distancia vertical desde el punto más alto del arco hasta la línea que une sus extremos) y el vano total. [23]
| 5 centros | 7 centros | 9 centros | ||||||
|---|---|---|---|---|---|---|---|---|
| Gota | 1er radio | Gota | 1er radio | 2do radio | Gota | 1er radio | 2do radio | 3er radio |
| 0,36 | 0,556 | 0,33 | 0,455 | 0,63 | 0,25 | 0,259 | 0,341 | 0,597 |
| 0,35 | 0,53 | 0,32 | 0,431 | 0,604 | 0,24 | 0,24 | 0,318 | 0,556 |
| 0,34 | 0,504 | 0,31 | 0,406 | 0,578 | 0,23 | 0,222 | 0,296 | 0,535 |
| 0,33 | 0,477 | 0,3 | 0,383 | 0,551 | 0,22 | 0,203 | 0,276 | 0,504 |
| 0,32 | 0,45 | 0,29 | 0,359 | 0,525 | 0,21 | 0,185 | 0,251 | 0,474 |
| 0,31 | 0,423 | 0,28 | 0,346 | 0,498 | 0,2 | 0,166 | 0,228 | 0,443 |
| 0,3 | 0,396 | 0,27 | 0,312 | 0,472 | ||||
| 0,26 | 0,289 | 0,445 | ||||||
| 0,25 | 0,265 | 0,419 | ||||||
La tabla que se proporciona permite la construcción sencilla de un arco con asa de cesta con cualquier abertura especificada utilizando cinco, siete o nueve centros, lo que elimina la necesidad de cálculos extensos. La única condición es que la caída debe coincidir con uno de los valores propuestos por Michal.
Por ejemplo, para dibujar una curva con siete centros, una abertura de 12 metros y una pendiente de 3 metros correspondiente a una caída de un cuarto (o 0,25), el primer y segundo radio se pueden calcular de la siguiente manera: 6×0,265 y 6×0,419, dando como resultado valores de 1,594 metros y 2,514 metros, respectivamente.
Para inscribir la curva dentro de un rectángulo denominado ABCD, se empezaría por describir un semicírculo en el segmento AB, que sirve de diámetro, y se dividiría en siete partes iguales. A continuación se trazarían las cuerdas Aa, ab, bc y cd, siendo la cuerda cd una semidivisión.
Sobre el eje AB, desde el punto A, se mide una longitud de 1,590 metros para establecer el primer centro, denominado m 1 . Por este punto se traza una paralela de radio O a que intersecta la cuerda Aa en el punto n, marcando el punto final del primer arco. Desde el punto n, se mide una longitud nm 2 igual a 2,514 metros para identificar el segundo centro, m 2 . Desde el punto m 2 se traza una paralela de radio O b , mientras que desde el punto n se traza una paralela a la cuerda ab . La intersección de estas dos paralelas en el punto n′ define el punto final del segundo arco. [24]
Continuando con este proceso, se traza una paralela a través del punto n′ hasta la cuerda bc, y desde el punto E, se traza una paralela hasta la cuerda cd. La intersección de estas dos líneas en el punto n′′ se utiliza para trazar una paralela al radio O c . Los puntos m 3 y m 4 , donde esta línea interseca las extensiones de radio n′m 2 y el eje vertical, se convierten en el tercer y cuarto centros. Los tres centros finales, m 5 , m 6 y m 7 , se posicionan simétricamente en relación con los primeros tres centros m 1 , m 2 y m 3 . [25]
Como se ilustra en la figura, los arcos An, nn′, n′n′′, etc., subtienden ángulos iguales en sus centros, específicamente 51° 34' 17" 14'. Además, la construcción de una semielipse con AB como eje mayor y OE como eje menor revela que los arcos de la semielipse, contenidos dentro de los mismos ángulos que los arcos circulares, poseen un radio de curvatura igual al de los arcos mismos.
Este método demuestra la facilidad con que se pueden construir curvas con cinco, siete o nueve centros.
El método Lerouge
Tras las aportaciones de Michal, el ingeniero jefe de Ponts et Chaussées, Lerouge, profundizó en el tema y elaboró tablas para construir curvas con tres, cinco, siete e incluso hasta quince centros.
Su planteamiento se aparta de la metodología de Michal al estipular que los radios sucesivos deben aumentar según una progresión aritmética. Este requisito implica que los ángulos formados entre los radios no tienen por qué ser necesariamente iguales, lo que permite una mayor flexibilidad en el diseño de las curvas.
Referencias
- ^ Hourihane 2012, pag. 130, Cesta.
- ^ Sociedad Técnica Americana 1920, pág. 395, Arco con asa de cesta.
- ^ Baker 1889, pág. 441.
- ^ Woodman y Bloom 2003, Deprimido.
- ^ Woodman & Bloom 2003, Cesta.
- ^ a b C Degrand & Resal (1887, pág. 363)
- ^ abcd Séjourné (1913c, pág.327)
- ^ Séjourné (1913a, págs.93, 97, 103)
- ^ Séjourné (1913a, pág. 107)
- ^ Séjourné (1913a, pág. 147)
- ^ Séjourné (1913a, pág. 122)
- ^ Séjourné (1913a, pág. 112)
- ^ Séjourné (1913a, pág. 110)
- ^ Séjourné (1913a, pág. 168)
- ^ Séjourné (1913a, pág. 103)
- ^ BENJAMIN LATROBE y el VIADUCTO THOMAS , The Maryland Surveyor, septiembre de 2000, págs. 20-28, [www.marylandsurveyor.org], consultado el 6 de abril de 2024 citando a Dilts, James D. (1996). The Great Road: The Building of the Baltimore and Ohio, the Nation's First Railroad, 1828–1853 . Palo Alto, CA: Stanford University Press. ISBN 978-0-8047-2629-0.Página 162.
- ^ ab Degrand y Resal (1887, pág. 364)
- ^ abc Prade (1986, pág. 11)
- ^ ab Degrand y Resal (1887, pág. 365)
- ^ Degrand y Resal (1887, pág.366)
- ^ ab Degrand y Resal (1887, pág. 367)
- ^ Degrand y Resal (1887, pág.368)
- ^ ab Degrand y Resal (1887, pág. 369)
- ^ Degrand y Resal (1887, pág.370)
- ^ Degrand y Resal (1887, pág.371)
Bibliografía
- "Aviso sur les courbes en anse de panier empleaées dans la construcción des ponts". Annales des ponts et chaussées. Mémoires et documents relatifs à l'art des Constructions et au service de l'ingénieur (en francés). Zoroastro Alexis Michal. París: Carilian-Goeury. 1831. 49-61.
{{cite book}}: CS1 maint: others (link) - "Mémoire sur les voûtes en anse de panier". Annales des ponts et chaussées. Mémoires et documents relatifs à l'art des Constructions et au service de l'ingénieur (en francés). Pierre-Jacques Lerouge. París: Carilian-Goeury. 1839, págs. 335–362.
{{cite book}}: CS1 maint: others (link) - Degrand, Eugenio; Resal, Jean (1887). Ponts en maçonnerie (en francés). vol. 2. París: Baudry.
- Séjourné, Paul (1913). Grandes Voûtes: Partie 1 - voûtes inarticulées (en francés). vol. 1. Bourges: Imprimerie Vve Tardy-Pigelet et fils.
- Séjourné, Paul (1913). Grandes Voûtes: voûtes inarticulées (suite) (en francés). vol. 3. Bourges: Imprimerie Vve Tardy-Pigelet et fils.
- Ministère des Transports, Dirección de rutas (1982). Les ponts en maçonnerie (PDF) (PDF) (en francés). Bagneux.
- Prade, Marcel (1986). Les Ponts, Monuments historiques: inventaire, descripción, histoire des ponts et ponts-aqueducs de France protégés au titre des monuments historiques (en francés). Brissaud. ISBN 978-2902170548.
- Prade, Marcel (1988). Ponts et Viaducs au xixe siècle (en francés). Brissaud. ISBN 978-2902170593.
- Prade, Marcel (1990). Los Grandes Puentes del Mundo. Ponts Remarquable d'Europe (en francés). Brissaud. ISBN 9782902170654.
- Woodman, Francis; Bloom, Jonathan M. (2003). "Arco". Oxford Art Online . Oxford University Press. doi :10.1093/gao/9781884446054.article.t003657. ISBN 978-1-884446-05-4.
- Sociedad Técnica Estadounidense (1920). «Arco con asa de cesta». Enciclopedia de ingeniería civil . Consultado el 5 de abril de 2024 .
- Baker, IO (1889). "Arco con asa de cesta". Tratado sobre construcción con mampostería . J. Wiley & sons . Consultado el 5 de abril de 2024 .
- Hourihane, C. (2012). "Arco". The Grove Encyclopedia of Medieval Art and Architecture . Vol. 1. Oxford University Press. págs. 129–134. ISBN 978-0-19-539536-5. Recuperado el 24 de diciembre de 2024 .