Vuelo de insectos

Los insectos son el único grupo de invertebrados que han desarrollado alas y capacidad de vuelo . Los insectos volaron por primera vez en el Carbonífero , hace unos 300 a 350 millones de años, lo que los convierte en los primeros animales en desarrollar el vuelo. Las alas pueden haber evolucionado a partir de apéndices en los lados de las extremidades existentes, que ya tenían nervios, articulaciones y músculos utilizados para otros fines. Es posible que inicialmente se hayan utilizado para navegar en el agua o para reducir la velocidad de descenso al planear.
Dos grupos de insectos, las libélulas y las efímeras , tienen músculos de vuelo unidos directamente a las alas. En otros insectos alados, los músculos de vuelo están unidos al tórax, lo que lo hace oscilar para inducir el batido de las alas. De estos insectos, algunos ( las moscas y algunos escarabajos ) alcanzan frecuencias de aleteo muy altas gracias a la evolución de un sistema nervioso "asincrónico", en el que el tórax oscila más rápido que la frecuencia de los impulsos nerviosos.
No todos los insectos son capaces de volar. Algunos insectos ápteros han perdido sus alas de forma secundaria a través de la evolución , mientras que otros insectos más basales , como los pececillos de plata, nunca desarrollaron alas. En algunos insectos eusociales , como las hormigas y las termitas , solo las castas reproductivas aladas desarrollan alas durante la temporada de apareamiento antes de perderlas después del apareamiento, mientras que los miembros de otras castas no tienen alas durante toda su vida.
Algunos insectos muy pequeños no utilizan la aerodinámica de estado estable , sino el mecanismo de aplauso y lanzamiento de Weis-Fogh, que genera grandes fuerzas de sustentación a costa del desgaste de las alas. Muchos insectos pueden flotar, manteniendo la altura y controlando su posición. Algunos insectos, como las polillas, tienen las alas delanteras acopladas a las traseras, de modo que pueden trabajar al unísono.
Mecanismos
Vuelo directo
A diferencia de otros insectos, los músculos de las alas de los efímeropteros (efímeras) y los odonatos (libélulas y caballitos del diablo) se insertan directamente en las bases de las alas, que están articuladas de modo que un pequeño movimiento hacia abajo de la base del ala eleva el ala hacia arriba, de manera muy similar a remar en el aire. Las libélulas y los caballitos del diablo tienen alas anteriores y posteriores de forma y tamaño similares. Cada una opera de manera independiente, lo que les otorga un grado de control fino y movilidad en términos de la brusquedad con la que pueden cambiar de dirección y velocidad, algo que no se observa en otros insectos voladores. Todos los odonatos son depredadores aéreos y siempre han cazado otros insectos aéreos. [1]
- Vuelo directo: músculos adheridos a las alas. Solo insectos grandes.
- Los odonatos (libélulas y caballitos del diablo) tienen musculatura de vuelo directa, al igual que las efímeras .
- Vuelo de libélula en cámara lenta
Vuelo indirecto
Aparte de los dos órdenes con músculos de vuelo directo, todos los demás insectos alados actuales vuelan utilizando un mecanismo diferente, que implica músculos de vuelo indirecto. Este mecanismo evolucionó una vez y es la característica definitoria ( sinapomorfia ) de la infraclase Neoptera ; corresponde, probablemente no por coincidencia, con la aparición de un mecanismo de plegado de las alas, que permite a los insectos Neoptera plegar las alas hacia atrás sobre el abdomen cuando están en reposo (aunque esta capacidad se ha perdido de forma secundaria en algunos grupos, como en las mariposas ). [1]
Sin embargo, lo que todos los Neoptera comparten es la forma en que funcionan los músculos del tórax : estos músculos, en lugar de unirse a las alas, se unen al tórax y lo deforman; dado que las alas son extensiones del exoesqueleto torácico , las deformaciones del tórax también hacen que las alas se muevan. Un conjunto de músculos longitudinales a lo largo de la espalda comprime el tórax de adelante hacia atrás, lo que hace que la superficie dorsal del tórax ( noto ) se arquee hacia arriba, haciendo que las alas se vuelquen hacia abajo. Otro conjunto de músculos desde el tergo hasta el esternón tira del noto hacia abajo nuevamente, lo que hace que las alas se vuelquen hacia arriba. [1] [2]
- Vuelo indirecto: los músculos hacen oscilar el tórax en la mayoría de los insectos
- Los neópteros , incluidas las mariposas y la mayoría de los demás insectos, tienen musculatura de vuelo indirecta.
Los insectos que baten sus alas menos de cien veces por segundo utilizan músculos sincrónicos, un tipo de músculo que se contrae una vez por cada impulso nervioso. Por lo general, esto produce menos potencia y es menos eficiente que el músculo asincrónico, lo que explica la evolución independiente de los músculos de vuelo asincrónicos en varios clados de insectos separados. [3]
Los insectos que baten sus alas más rápidamente, como el abejorro , utilizan músculos asincrónicos; se trata de un tipo de músculo que se contrae más de una vez por impulso nervioso. Esto se logra estimulando el músculo para que se contraiga nuevamente mediante una liberación de la tensión en el músculo, lo que puede suceder más rápidamente que mediante una simple estimulación nerviosa sola. [4] Esto permite que la frecuencia de los batidos de las alas supere la velocidad a la que el sistema nervioso puede enviar impulsos. El músculo asincrónico es uno de los refinamientos finales que ha aparecido en algunos de los neópteros superiores ( coleópteros , dípteros e himenópteros ). El efecto general es que muchos neópteros superiores pueden batir sus alas mucho más rápido que los insectos con músculos de vuelo directo. [1]
Por definición, los músculos asincrónicos están bajo un control relativamente burdo del sistema nervioso. Para equilibrar esta compensación evolutiva, los insectos que desarrollaron el vuelo indirecto también desarrollaron un sistema neuromuscular separado para el control de grano fino del movimiento de las alas. [5] Estos músculos, conocidos como "músculos directos", se adhieren directamente a los escleritos que forman la bisagra del ala y se contraen con impulsos 1:1 de las neuronas motoras. [6] Los trabajos recientes han comenzado a abordar la dinámica muscular no lineal compleja en la bisagra del ala y sus efectos en la trayectoria de la punta del ala. [7]
Aerodinámica
Hay dos modelos aerodinámicos básicos del vuelo de los insectos: la creación de un vórtice en el borde de ataque y el uso de aplausos y lanzamientos. [8] [9]
Vórtice de vanguardia
La mayoría de los insectos utilizan un método que crea un vórtice en espiral en el borde delantero . Estas alas batientes se mueven a través de dos semirrevoluciones básicas. La revoluciones descendentes comienzan hacia arriba y hacia atrás y se hunden hacia abajo y hacia adelante. Luego, el ala se voltea rápidamente ( supinación ) de modo que el borde delantero apunte hacia atrás. Luego, la revoluciones ascendentes empujan el ala hacia arriba y hacia atrás. Luego, el ala se voltea nuevamente ( pronación ) y puede ocurrir otra revoluciones descendentes. El rango de frecuencia en insectos con músculos de vuelo sincrónicos es típicamente de 5 a 200 hercios (Hz). En aquellos con músculos de vuelo asincrónicos, la frecuencia de batido de alas puede superar los 1000 Hz. Cuando el insecto está suspendido en el aire, las dos revoluciones duran la misma cantidad de tiempo. Sin embargo, una revoluciones descendentes más lentas proporciona empuje . [8] [9]
La identificación de las fuerzas principales es fundamental para comprender el vuelo de los insectos. Los primeros intentos de comprender el aleteo de las alas asumieron un estado cuasi estable. Esto significa que se supuso que el flujo de aire sobre el ala en un momento dado era el mismo que el flujo sobre un ala estable sin aleteo en el mismo ángulo de ataque. Al dividir el ala batiente en una gran cantidad de posiciones inmóviles y luego analizar cada posición, sería posible crear una línea de tiempo de las fuerzas instantáneas sobre el ala en cada momento. Se descubrió que la sustentación calculada era demasiado pequeña por un factor de tres, por lo que los investigadores se dieron cuenta de que debía haber fenómenos inestables que generaran fuerzas aerodinámicas. Hubo varios modelos analíticos en desarrollo que intentaban aproximarse al flujo cerca de un ala batiente. Algunos investigadores predijeron picos de fuerza en la supinación. Con un modelo a escala dinámica de una mosca de la fruta , estas fuerzas predichas se confirmaron más tarde. Otros argumentaron que los picos de fuerza durante la supinación y la pronación son causados por un efecto rotacional desconocido que es fundamentalmente diferente de los fenómenos de traslación. Existe cierto desacuerdo con este argumento. Algunos investigadores, a través de la dinámica de fluidos computacional , sostienen que no existe efecto rotacional y sostienen que las altas fuerzas son causadas por una interacción con la estela desprendida por el golpe anterior. [8] [9]
De manera similar al efecto rotacional mencionado anteriormente, los fenómenos asociados con el aleteo de alas no se comprenden completamente ni hay consenso al respecto. Debido a que cada modelo es una aproximación, diferentes modelos dejan de lado efectos que se presumen insignificantes. Por ejemplo, el efecto Wagner , propuesto por Herbert A. Wagner en 1925, [10] dice que la circulación aumenta lentamente hasta su estado estable debido a la viscosidad cuando un ala inclinada se acelera desde el reposo. Este fenómeno explicaría un valor de sustentación menor que el predicho. Por lo general, el caso ha sido encontrar fuentes para la sustentación adicional. Se ha argumentado que este efecto es insignificante para el flujo con un número de Reynolds que es típico del vuelo de los insectos. El número de Reynolds es una medida de turbulencia ; el flujo es laminar (suave) cuando el número de Reynolds es bajo y turbulento cuando es alto. [11] El efecto Wagner fue ignorado, conscientemente, en al menos un modelo. [9] Uno de los fenómenos más importantes que se producen durante el vuelo de los insectos es la succión del borde de ataque. Esta fuerza es significativa para el cálculo de la eficiencia. El concepto de succión del borde de ataque fue propuesto por primera vez por DG Ellis y JL Stollery en 1988 para describir la sustentación del vórtice en alas delta de bordes afilados . [12] En ángulos de ataque altos, el flujo se separa sobre el borde de ataque, pero se vuelve a unir antes de alcanzar el borde de salida. Dentro de esta burbuja de flujo separado hay un vórtice. Debido a que el ángulo de ataque es tan alto, se transfiere mucho impulso hacia abajo en el flujo. Estas dos características crean una gran cantidad de fuerza de sustentación, así como algo de resistencia adicional. Sin embargo, la característica importante es la sustentación. Debido a que el flujo se ha separado, pero aún proporciona grandes cantidades de sustentación, este fenómeno se llama retraso de pérdida , observado por primera vez en las hélices de los aviones por H. Himmelskamp en 1945. [13] Este efecto se observó en el vuelo de insectos aleteando y se demostró que era capaz de proporcionar suficiente sustentación para explicar la deficiencia en los modelos de estado cuasi-estacionario. Este efecto es utilizado por los piragüistas en una palada de remo . [8] [9]
Todos los efectos sobre un ala batiente pueden reducirse a tres fuentes principales de fenómenos aerodinámicos: el vórtice del borde de ataque, las fuerzas aerodinámicas de estado estable sobre el ala y el contacto del ala con su estela de aleteos anteriores. El tamaño de los insectos voladores varía de unos 20 microgramos a unos 3 gramos. A medida que aumenta la masa corporal del insecto, aumenta el área del ala y disminuye la frecuencia de aleteo. Para los insectos más grandes, el número de Reynolds (Re) puede ser tan alto como 10000, donde el flujo comienza a volverse turbulento. Para los insectos más pequeños, puede ser tan bajo como 10. Esto significa que los efectos viscosos son mucho más importantes para los insectos más pequeños. [9] [14] [15]
Otra característica interesante del vuelo de los insectos es la inclinación del cuerpo. A medida que aumenta la velocidad de vuelo, el cuerpo del insecto tiende a inclinarse hacia abajo y volverse más horizontal. Esto reduce el área frontal y, por lo tanto, la resistencia del cuerpo. Dado que la resistencia también aumenta a medida que aumenta la velocidad hacia adelante, el insecto hace que su vuelo sea más eficiente, ya que esta eficiencia se vuelve más necesaria. Además, al cambiar el ángulo geométrico de ataque en la carrera descendente, el insecto puede mantener su vuelo con una eficiencia óptima a través de tantas maniobras como sea posible. El desarrollo del empuje general es relativamente pequeño en comparación con las fuerzas de sustentación. Las fuerzas de sustentación pueden ser más de tres veces el peso del insecto, mientras que el empuje incluso a las velocidades más altas puede ser tan bajo como el 20% del peso. Esta fuerza se desarrolla principalmente a través de la carrera ascendente menos potente del movimiento de aleteo. [9] [16]
Aplaudir y lanzar
El mecanismo Weis-Fogh, descubierto por el zoólogo danés Torkel Weis-Fogh , es un método de generación de sustentación utilizado durante el vuelo de insectos pequeños. [17] A medida que el tamaño de los insectos se vuelve inferior a 1 mm, las fuerzas viscosas se vuelven dominantes y la eficacia de la generación de sustentación de un perfil aerodinámico disminuye drásticamente. Partiendo de la posición de aplauso, las dos alas se separan y giran sobre el borde de salida. Luego, las alas se separan y barren horizontalmente hasta el final de la carrera descendente. A continuación, las alas se pronan y utilizan el borde de ataque durante un movimiento de remo ascendente. A medida que comienza el movimiento de aplauso, los bordes de ataque se encuentran y giran juntos hasta que el espacio desaparece. Inicialmente, se pensó que las alas se tocaban, pero varios incidentes indican un espacio entre las alas y sugieren que proporciona un beneficio aerodinámico. [18] [19]
La generación de sustentación a partir del mecanismo de aplauso y lanzamiento ocurre durante varios procesos a lo largo del movimiento. Primero, el mecanismo se basa en una interacción ala-ala, ya que un solo movimiento de ala no produce suficiente sustentación. [20] [21] [22] A medida que las alas giran sobre el borde de salida en el movimiento de lanzamiento, el aire se precipita hacia el espacio creado y genera un fuerte vórtice en el borde de entrada y un segundo vórtice que se desarrolla en las puntas de las alas. Un tercer vórtice, más débil, se desarrolla en el borde de salida. [19] La fuerza de los vórtices en desarrollo depende, en parte, del espacio inicial de la separación entre alas al comienzo del movimiento de lanzamiento. Con un espacio entre alas reducido, se indica una mayor generación de sustentación, a costa de mayores fuerzas de arrastre. Se descubrió que la implementación de un movimiento de levantamiento durante el lanzamiento, [23] alas flexibles, [21] y un mecanismo de pérdida retardada refuerzan la estabilidad y la unión del vórtice. [24] Finalmente, para compensar la menor producción de sustentación general durante el vuelo con bajo número de Reynolds (con flujo laminar ), los insectos diminutos a menudo tienen una frecuencia de golpe más alta para generar velocidades en la punta del ala que son comparables a las de los insectos más grandes. [24]
Las mayores fuerzas de arrastre previstas se producen durante el movimiento de lanzamiento dorsal, ya que las alas necesitan separarse y rotar. [22] La atenuación de las grandes fuerzas de arrastre se produce a través de varios mecanismos. Se ha descubierto que las alas flexibles reducen la resistencia en el movimiento de lanzamiento hasta en un 50% y reducen aún más la resistencia general durante todo el recorrido del ala en comparación con las alas rígidas. [21] Las cerdas en los bordes de las alas, como se ve en Encarsia formosa , provocan una porosidad en el flujo que aumenta y reduce las fuerzas de arrastre, a costa de una menor generación de sustentación. [25] Además, la separación entre alas antes del lanzamiento juega un papel importante en el efecto general de la resistencia. A medida que aumenta la distancia entre las alas, la resistencia general disminuye. [18]
El mecanismo de aplauso y lanzamiento también lo emplea el molusco marino Limacina helicina , una mariposa marina. [26] [27] Algunos insectos, como el minador de hojas vegetales Liriomyza sativae (una mosca), explotan un aplauso y lanzamiento parcial, usando el mecanismo solo en la parte exterior del ala para aumentar la sustentación en un 7% aproximadamente cuando se ciernen. [24]
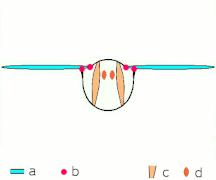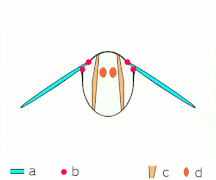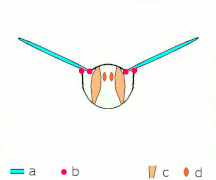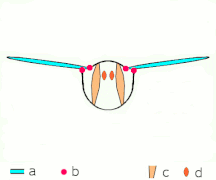
- Mecanismo de vuelo de aplausos y lanzamientos según Sane 2003
- Aplaudir 1: las alas se cierran sobre la espalda
- Aplaudir 2: los bordes de ataque se tocan, el ala gira alrededor del borde de ataque , se forman vórtices
- Aplaudir 3: los bordes de salida se cierran, los vórtices se desprenden, las alas se cierran dando empuje
- Flechas negras (curvas): flujo; Flechas azules: velocidad inducida; Flechas naranjas: fuerza neta sobre el ala
- Lanzamiento 1: las alas giran alrededor del borde posterior para separarse.
- Lanzamiento 2: el borde de ataque se aleja, el aire entra rápidamente y aumenta la sustentación.
- Fling 3: se forman nuevos vórtices en el borde de ataque, los vórtices del borde de salida se cancelan entre sí, lo que tal vez ayude a que el flujo crezca más rápido ( Weis-Fogh 1973)
Ecuaciones de gobierno
Un ala que se mueve en fluidos experimenta una fuerza de fluido , que sigue las convenciones que se encuentran en la aerodinámica. El componente de fuerza normal a la dirección del flujo en relación con el ala se llama sustentación ( L ), y el componente de fuerza en la dirección opuesta del flujo es resistencia ( D ). En los números de Reynolds considerados aquí, una unidad de fuerza apropiada es 1/2(ρU 2 S), donde ρ es la densidad del fluido, S el área del ala y U la velocidad del ala. Las fuerzas adimensionales se denominan coeficientes de sustentación ( C L ) y resistencia ( C D ), es decir: [8]
C L y C D son constantes sólo si el flujo es constante. Una clase especial de objetos como los perfiles aerodinámicos pueden alcanzar un estado constante cuando atraviesan el fluido con un ángulo de ataque pequeño. En este caso, el flujo no viscoso alrededor de un perfil aerodinámico puede aproximarse mediante un flujo potencial que satisface la condición de contorno de no penetración. El teorema de Kutta-Joukowski de un perfil aerodinámico 2D supone además que el flujo sale del borde de salida afilado de forma suave, y esto determina la circulación total alrededor de un perfil aerodinámico. La sustentación correspondiente viene dada por el principio de Bernoulli ( teorema de Blasius ): [8]
Los flujos alrededor de aves e insectos pueden considerarse incompresibles : el número de Mach , o velocidad relativa a la velocidad del sonido en el aire, es típicamente 1/300 y la frecuencia del ala es de aproximadamente 10–103 Hz. Usando la ecuación gobernante como la ecuación de Navier-Stokes sujeta a la condición de contorno sin deslizamiento, la ecuación es: [8]
Donde u (x, t) es el campo de flujo, p la presión, ρ la densidad del fluido, ν la viscosidad cinemática, u bd la velocidad en el límite y u s la velocidad del sólido. Al elegir una escala de longitud, L, y una escala de velocidad, U, la ecuación se puede expresar en forma adimensional que contiene el número de Reynolds, R e = uL/ν . Hay dos diferencias obvias entre el ala de un insecto y un perfil aerodinámico: el ala de un insecto es mucho más pequeña y aletea. Usando una libélula como ejemplo, su cuerda (c) es de aproximadamente 1 cm (0,39 pulgadas), su longitud de ala (l) de aproximadamente 4 cm (1,6 pulgadas) y su frecuencia de ala (f) de aproximadamente 40 Hz. La velocidad de la punta (u) es de aproximadamente 1 m/s (3,3 pies/s), y el número de Reynolds correspondiente es de aproximadamente 103. En el extremo más pequeño, una avispa calcidoide típica tiene una longitud de ala de aproximadamente 0,5–0,7 mm (0,020–0,028 pulgadas) y bate sus alas a aproximadamente 400 Hz. Su número de Reynolds es de aproximadamente 25. El rango del número de Reynolds en el vuelo de los insectos es de aproximadamente 10 a 10 4 , que se encuentra entre los dos límites que son convenientes para las teorías: flujos constantes no viscosos alrededor de un perfil aerodinámico y flujo de Stokes experimentado por una bacteria nadadora. Por esta razón, este rango intermedio no se entiende bien. Por otro lado, es quizás el régimen más ubicuo entre las cosas que vemos. Las hojas y semillas que caen, los peces y los pájaros se encuentran con flujos inestables similares al que se ve alrededor de un insecto. [8] El número de Reynolds en el sentido de la cuerda se puede describir por:
y
Donde es la longitud media de la cuerda, es la velocidad de la punta del ala, es la amplitud de la carrera, es la frecuencia de batido, es el radio de giro, es el área del ala y es la longitud del ala, incluida la punta del ala.
Además del número de Reynolds, hay al menos otros dos parámetros adimensionales relevantes. Un ala tiene tres escalas de velocidad: la velocidad de aleteo con respecto al cuerpo ( u ), la velocidad de avance del cuerpo ( U 0 ) y la velocidad de cabeceo (Ω c ). Las relaciones entre ellas forman dos variables adimensionales, U 0 / u y Ωc/ u , la primera se suele denominar relación de avance, y también está relacionada con la frecuencia reducida, fc / U 0 . [8]
Si el ala de un insecto es rígida, por ejemplo, el ala de una Drosophila lo es aproximadamente, su movimiento relativo a un cuerpo fijo se puede describir mediante tres variables: la posición de la punta en coordenadas esféricas , (Θ(t),Φ(t)), y el ángulo de inclinación ψ(t), sobre el eje que conecta la raíz y la punta. Para estimar las fuerzas aerodinámicas basadas en el análisis de elementos de la pala, también es necesario determinar el ángulo de ataque (α). El ángulo de ataque típico con una envergadura del 70% varía de 25° a 45° en insectos que flotan (15° en colibríes). A pesar de la gran cantidad de datos disponibles para muchos insectos, relativamente pocos experimentos informan sobre la variación temporal de α durante un vuelo. Entre ellos se encuentran experimentos en túnel de viento de una langosta atada y una mosca atada, y el vuelo libre en vuelo de una mosca de la fruta. [8]
Debido a que son relativamente fáciles de medir, las trayectorias de las puntas de las alas se han reportado con mayor frecuencia. Por ejemplo, al seleccionar solo secuencias de vuelo que produjeron suficiente sustentación para soportar un peso, se mostrará que la punta del ala sigue una forma elíptica. También se reportaron formas que no se cruzan para otros insectos. Independientemente de sus formas exactas, el movimiento de caída indica que los insectos pueden usar la resistencia aerodinámica además de la sustentación para soportar su peso. [8]
Flotando
| Parámetros de vuelo [28] | Velocidad (m/s) | Latidos/s |
|---|---|---|
| Libélula Aeshnid | 7.0 | 38 |
| Avispón | 5.7 | 100 |
| Polilla halcón colibrí | 5.0 | 85 |
| Tábano | 3.9 | 96 |
| Mosca sírfida | 3.5 | 120 |
| Abejorro | 2.9 | 130 |
| Abeja melífera | 2.5 | 250 |
| Mosca doméstica | 2.0 | 190 |
| Caballito del diablo | 1.5 | 16 |
| Mosca escorpión | 0,49 | 28 |
| Mariposa blanca grande [29] | 2.5 | 12 |
| Trips (aplauden y lanzan) [24] | 0.3 | 254 |
.jpg/440px-Hoverfly_September_2007-7_(cropped).jpg)
Muchos insectos pueden flotar o permanecer en un punto en el aire batiendo rápidamente sus alas. Para ello es necesario estabilizarse lateralmente y generar sustentación. La fuerza de sustentación se produce principalmente mediante el movimiento descendente. A medida que las alas empujan hacia abajo el aire circundante, la fuerza de reacción resultante del aire sobre las alas empuja al insecto hacia arriba. Las alas de la mayoría de los insectos están diseñadas de manera que, durante el movimiento ascendente, la fuerza sobre el ala es pequeña. Dado que el movimiento descendente y el movimiento de retorno fuerzan al insecto hacia arriba y hacia abajo respectivamente, el insecto oscila y termina permaneciendo en la misma posición. [14]
La distancia que recorre el insecto entre aleteos depende de la velocidad con la que bate las alas: cuanto más lento aletea, más largo es el intervalo en el que cae y más lejos cae entre cada aleteo. Se puede calcular la frecuencia de aleteo necesaria para que el insecto mantenga una estabilidad dada en su amplitud. Para simplificar los cálculos, hay que suponer que la fuerza de sustentación tiene un valor constante finito mientras las alas se mueven hacia abajo y que es cero mientras las alas se mueven hacia arriba. Durante el intervalo de tiempo Δ t del aleteo ascendente, el insecto cae una distancia h bajo la influencia de la gravedad. [14]
El movimiento ascendente devuelve al insecto a su posición original. Normalmente, puede ser necesario que la posición vertical del insecto no cambie más de 0,1 mm (es decir, h = 0,1 mm). El tiempo máximo permitido para la caída libre es entonces [14]
Dado que los movimientos ascendentes y descendentes de las alas tienen una duración aproximadamente igual, el período T para un ala completa hacia arriba y hacia abajo es el doble de Δ r , es decir, [14]
La frecuencia de los batidos, f, es decir, el número de aleteos por segundo, se representa mediante la ecuación: [14]
En los ejemplos utilizados, la frecuencia utilizada es de 110 pulsaciones/s, que es la frecuencia típica que se encuentra en los insectos. Las mariposas tienen una frecuencia mucho más lenta, de aproximadamente 10 pulsaciones/s, lo que significa que no pueden flotar. Otros insectos pueden ser capaces de producir una frecuencia de 1000 pulsaciones/s. Para devolver al insecto a su posición vertical original, la fuerza ascendente media durante el movimiento descendente, F av , debe ser igual al doble del peso del insecto. Nótese que, dado que la fuerza ascendente sobre el cuerpo del insecto se aplica solo durante la mitad del tiempo, la fuerza ascendente media sobre el insecto es simplemente su peso. [14]
Entrada de potencia
Ahora se puede calcular la potencia necesaria para mantener el vuelo, considerando de nuevo un insecto con masa m 0,1 g, la fuerza media, F av , aplicada por las dos alas durante el movimiento descendente es dos veces el peso. Debido a que la presión aplicada por las alas se distribuye uniformemente sobre el área total del ala, eso significa que se puede suponer que la fuerza generada por cada ala actúa a través de un único punto en la sección media de las alas. Durante el movimiento descendente, el centro de las alas recorre una distancia vertical d . [14] El trabajo total realizado por el insecto durante cada movimiento descendente es el producto de la fuerza y la distancia; es decir,
Si las alas oscilan durante el movimiento de aleteo en un ángulo de 70°, entonces, en el caso presentado para el insecto con alas de 1 cm de largo, d es 0,57 cm. Por lo tanto, el trabajo realizado durante cada movimiento de aleteo por las dos alas es: [14]
La energía se utiliza para elevar el insecto contra la gravedad. La energía E necesaria para elevar la masa del insecto 0,1 mm durante cada carrera descendente es: [14]
Esta es una fracción insignificante de la energía total gastada, que claramente, la mayor parte de la energía se gasta en otros procesos. Un análisis más detallado del problema muestra que el trabajo realizado por las alas se convierte principalmente en energía cinética del aire que se acelera por el movimiento descendente de las alas. La potencia es la cantidad de trabajo realizado en 1 s; en el insecto utilizado como ejemplo, realiza 110 movimientos descendentes por segundo. Por lo tanto, su potencia de salida P es de movimientos por segundo, y eso significa que su potencia de salida P es: [14]
Potencia de salida
En el cálculo de la potencia empleada para mantenerse en el aire, los ejemplos utilizados no tuvieron en cuenta la energía cinética de las alas en movimiento. Las alas de los insectos, por ligeras que sean, tienen una masa finita; por lo tanto, al moverse poseen energía cinética. Como las alas están en movimiento rotatorio, la energía cinética máxima durante cada aleteo es: [14]
Aquí I es el momento de inercia del ala y ω max es la velocidad angular máxima durante el movimiento del ala. Para obtener el momento de inercia del ala, supondremos que el ala puede aproximarse mediante una varilla delgada pivotada en un extremo. El momento de inercia del ala es entonces: [14]
Donde l es la longitud del ala (1 cm) y m es la masa de las dos alas, que normalmente puede ser de 10 −3 g. La velocidad angular máxima, ω max , se puede calcular a partir de la velocidad lineal máxima , ν max , en el centro del ala: [14]
Durante cada carrera, el centro de las alas se mueve con una velocidad lineal media ν av dada por la distancia d recorrida por el centro del ala dividida por la duración Δt de la carrera del ala. De nuestro ejemplo anterior, d = 0,57 cm y Δt = 4,5×10 −3 s. Por lo tanto: [14]
La velocidad de las alas es cero tanto al principio como al final de la carrera del ala, lo que significa que la velocidad lineal máxima es mayor que la velocidad media. Si suponemos que la velocidad oscila ( sinusoidalmente ) a lo largo de la trayectoria del ala, la velocidad máxima es el doble de alta que la velocidad media. Por lo tanto, la velocidad angular máxima es: [14]
Y por lo tanto la energía cinética es: [14]
Como en cada ciclo del movimiento del ala hay dos movimientos (ascendente y descendente), la energía cinética es 2×43 = 86 erg . Esta es aproximadamente la misma energía que se consume en el propio vuelo estacionario. [14]
Elasticidad

Los insectos obtienen energía cinética, proporcionada por los músculos, cuando las alas aceleran . Cuando las alas comienzan a desacelerar hacia el final del movimiento, esta energía debe disiparse. Durante el movimiento descendente, la energía cinética es disipada por los propios músculos y se convierte en calor (este calor a veces se utiliza para mantener la temperatura corporal central). Algunos insectos pueden utilizar la energía cinética en el movimiento ascendente de las alas para ayudar en su vuelo. Las articulaciones de las alas de estos insectos contienen una almohadilla de proteína elástica, similar al caucho, llamada resilina . Durante el movimiento ascendente del ala, la resilina se estira. La energía cinética del ala se convierte en energía potencial en la resilina estirada, que almacena la energía de manera muy similar a un resorte. Cuando el ala se mueve hacia abajo, esta energía se libera y ayuda en el movimiento descendente. [14]
Utilizando algunas suposiciones simplificadoras, podemos calcular la cantidad de energía almacenada en la resilina estirada. Aunque la resilina se dobla en una forma compleja, el ejemplo dado muestra el cálculo como una varilla recta de área A y longitud. Además, supondremos que durante todo el estiramiento la resilina obedece la ley de Hooke . Esto no es estrictamente cierto ya que la resilina se estira en una cantidad considerable y, por lo tanto, tanto el área como el módulo de Young cambian en el proceso de estiramiento. La energía potencial U almacenada en la resilina estirada es: [14]
Aquí E es el módulo de Young para la resilina, que se ha medido como 1,8×10 7 dyn /cm 2 . Normalmente, en un insecto del tamaño de una abeja, el volumen de la resilina puede ser equivalente a un cilindro de 2×10 −2 cm de largo y 4×10 −4 cm 2 de área. En el ejemplo dado, la longitud de la varilla de resilina aumenta en un 50% cuando se estira. Es decir, Δℓ es 10 −2 cm. Por lo tanto, en este caso la energía potencial almacenada en la resilina de cada ala es: [14]
La energía almacenada en las dos alas de un insecto del tamaño de una abeja es de 36 erg, lo que es comparable a la energía cinética del movimiento ascendente de las alas. Los experimentos muestran que hasta el 80% de la energía cinética del ala puede almacenarse en la resilina. [14]
Acoplamiento de ala

Algunos órdenes de insectos de cuatro alas, como los lepidópteros, han desarrollado mecanismos morfológicos de acoplamiento de alas en el imago que hacen que estos taxones sean funcionalmente de dos alas. [30] Todas las formas, excepto las más basales, exhiben este acoplamiento de alas. [31]
Los mecanismos son de tres tipos diferentes: yugal, frenulo-retinacular y amplexiforme: [32]
- Los grupos más primitivos tienen un área agrandada similar a un lóbulo cerca del margen posterior basal, es decir, en la base del ala anterior, unjugum , que se pliega debajo del ala trasera durante el vuelo. [31] [33]
- Otros grupos tienen un frenillo en el ala trasera que se engancha debajo de un retináculo en el ala delantera. [33]
- En casi todas las mariposas y en los Bombycoidea (excepto los Sphingidae ), no existe una disposición de frenillo y retináculo para acoplar las alas. En cambio, una zona humeral agrandada del ala posterior se superpone ampliamente con el ala anterior. A pesar de la ausencia de una conexión mecánica específica, las alas se superponen y operan en fase. El golpe de potencia del ala anterior empuja hacia abajo el ala posterior al unísono. Este tipo de acoplamiento es una variación del tipo frenético pero donde el frenillo y el retináculo se pierden por completo. [30] [34]
Bioquímica
La bioquímica del vuelo de los insectos ha sido objeto de numerosos estudios. Si bien muchos insectos utilizan carbohidratos y lípidos como fuente de energía para volar, muchos escarabajos y moscas utilizan el aminoácido prolina como fuente de energía. [35] Algunas especies también utilizan una combinación de fuentes y las polillas como Manduca sexta utilizan carbohidratos para calentarse antes del vuelo. [36]
Retroalimentación sensorial
Los insectos utilizan la retroalimentación sensorial para mantener y controlar el vuelo. Los insectos controlan la postura de vuelo, la amplitud y la frecuencia del aleteo utilizando información de sus antenas [37] , halterios [38] y alas [39].
Evolución y adaptación

En algún momento del Período Carbonífero , hace unos 350 a 300 millones de años, cuando solo había dos grandes masas de tierra, los insectos comenzaron a volar. [40] Entre los fósiles de insectos alados más antiguos se encuentra Delitzschala , un paleodictióptero del Carbonífero Inferior; [41] Rhyniognatha es más antiguo, del Devónico Temprano , pero no se sabe con certeza si tenía alas o si era un insecto. [42] [43]
No se entiende bien cómo y por qué se desarrollaron las alas de los insectos, en gran parte debido a la escasez de fósiles apropiados del período de su desarrollo en el Carbonífero Inferior. Históricamente ha habido tres teorías principales sobre los orígenes del vuelo de los insectos. La primera fue que son modificaciones de las branquias abdominales móviles , como las que se encuentran en las náyades acuáticas de las efímeras . El análisis filogenómico sugiere que los polineópteros , el grupo de insectos alados que incluye a los saltamontes, evolucionaron a partir de un ancestro terrestre, lo que hace poco probable la evolución de las alas a partir de las branquias. [44] Un estudio adicional del comportamiento de salto de las larvas de efímera ha determinado que las branquias traqueales no juegan ningún papel en la guía del descenso de los insectos, lo que proporciona más evidencia en contra de esta hipótesis evolutiva. [45] Esto deja dos teorías históricas principales: que las alas se desarrollaron a partir de lóbulos paranotales, extensiones de los terga torácicos ; o que surgieron de modificaciones de los segmentos de las patas, que ya contenían músculos. [46]
Hipótesis de la epicoxal (branquias abdominales)
.JPG/440px-Mayfly_nymph_dorsal_view_wing_buds_paired_gills_(rotated).JPG)
Numerosos entomólogos, entre ellos Landois en 1871, Lubbock en 1873, Graber en 1877 y Osborn en 1905, han sugerido que un posible origen de las alas de los insectos podrían haber sido las branquias abdominales móviles que se encuentran en muchos insectos acuáticos, como las náyades de las efímeras. Según esta teoría, estas branquias traqueales , que en un principio eran salidas del sistema respiratorio y con el tiempo se modificaron para funciones locomotoras, acabaron convirtiéndose en alas. Las branquias traqueales están equipadas con pequeñas aletas que vibran permanentemente y tienen sus propios músculos rectos diminutos. [48]
Hipótesis paranotal (tergal)
La hipótesis del lóbulo paranotal o tergal (pared dorsal del cuerpo), propuesta por Fritz Müller en 1875 [49] y reelaborada por G. Crampton en 1916, [47] Jarmila Kukalova-Peck en 1978 [50] y Alexander P. Rasnitsyn en 1981 entre otros, [51] sugiere que las alas del insecto se desarrollaron a partir de lóbulos paranotales, una preadaptación encontrada en fósiles de insectos que habría ayudado a la estabilización durante los saltos o las caídas. A favor de esta hipótesis está la tendencia de la mayoría de los insectos, cuando se asustan mientras trepan por las ramas, a escapar dejándose caer al suelo. Estos lóbulos habrían servido como paracaídas y habrían permitido al insecto aterrizar más suavemente. La teoría sugiere que estos lóbulos gradualmente se hicieron más grandes y en una etapa posterior desarrollaron una articulación con el tórax. Incluso más tarde aparecerían los músculos para mover estas rudimentarias alas. Este modelo implica un aumento progresivo de la eficacia de las alas, comenzando con el paracaidismo , luego el planeo y finalmente el vuelo activo . Aun así, la falta de evidencia fósil sustancial del desarrollo de las articulaciones y músculos de las alas plantea una gran dificultad a la teoría, al igual que el desarrollo aparentemente espontáneo de la articulación y la venación, y ha sido ampliamente rechazada por los expertos en el campo. [48]
Hipótesis de endite-exite (pleural)

En 1990, JWH Trueman propuso que el ala era una adaptación de los endites y los exites , apéndices en los respectivos aspectos internos y externos de la extremidad primitiva del artrópodo , también llamada hipótesis pleural. Esto se basó en un estudio de Goldschmidt en 1945 sobre Drosophila melanogaster , en el que una variación llamada "pod" (por podómeros, segmentos de las extremidades) mostró una mutación que transformó las alas normales. El resultado se interpretó como una disposición de patas de triple articulación con algunos apéndices adicionales pero sin el tarso, donde normalmente estaría la superficie costal del ala. Esta mutación se reinterpretó como una fuerte evidencia de una fusión de exite dorsal y endite, en lugar de una pata, con los apéndices encajando mucho mejor con esta hipótesis. La inervación, la articulación y la musculatura necesarias para la evolución de las alas ya están presentes en los segmentos de las extremidades. [46]
Otras hipótesis
Otras hipótesis incluyen la sugerencia de Vincent Wigglesworth de 1973 de que las alas se desarrollaron a partir de protuberancias torácicas utilizadas como radiadores . [48]
Adrian Thomas y Åke Norberg sugirieron en 2003 que las alas pueden haber evolucionado inicialmente para navegar en la superficie del agua como se ve en algunas moscas de piedra . [52] [53]
Stephen P. Yanoviak y sus colegas propusieron en 2009 que el ala se deriva del descenso aéreo planeado dirigido, un fenómeno previo al vuelo que se encuentra en algunos apterygota , un taxón hermano sin alas de los insectos alados. [54]
Origen dual
Biólogos como Averof, [55] Niwa, [56] Elias-Neto [57] y sus colegas han comenzado a explorar el origen del ala de los insectos utilizando evo-devo además de evidencia paleontológica. Esto sugiere que las alas son homólogas en serie con las estructuras tergales y pleurales, lo que potencialmente resuelve el debate de siglos de antigüedad. [58] Jakub Prokop y sus colegas encontraron en 2017 evidencia paleontológica de las almohadillas de las alas de las ninfas del Paleozoico de que las alas efectivamente tenían ese origen dual. [59]
Véase también
Referencias
- ^ abcd Chapman, AD (2006). Número de especies vivas en Australia y el mundo. Canberra: Estudio de los recursos biológicos de Australia . pp. 60pp. ISBN 978-0-642-56850-2Archivado desde el original el 19 de mayo de 2009. Consultado el 15 de septiembre de 2015 .
- ^ Smith, DS (1965). "Músculos de vuelo de los insectos". Scientific American . 212 (6): 76–88. Bibcode :1965SciAm.212f..76S. doi :10.1038/scientificamerican0665-76. PMID 14327957.
- ^ Josephson, Robert K.; Malamud, Jean G.; Stokes, Darrell R. (2001). "La eficiencia de un músculo de vuelo asincrónico de un escarabajo". The Journal of Experimental Biology . 204 (23): 4125–4139. doi :10.1242/jeb.204.23.4125. PMID 11809787.
- ^ "Definición de músculo asincrónico en el glosario de entomólogos". Departamento de Entomología, Universidad Estatal de Carolina del Norte . Consultado el 21 de marzo de 2011 .
- ^ Deora, Tanvi; Gundiah, Namrata; Sane, Sanjay P. (15 de abril de 2017). "Mecánica del tórax en moscas". Revista de biología experimental . 220 (8): 1382–1395. doi : 10.1242/jeb.128363 . PMID 28424311. S2CID 207172023.
- ^ Heide, GG (1983). "Mecanismos neuronales de control de vuelo en Diptera". En Nachtigall, Werner (ed.). Informe BIONA . vol. 2: Vuelo de insectos II. Stuttgart: Gustav Fischer. págs. 33–52.
- ^ Melis, Johan M.; Dickinson, Michael H. (30 de junio de 2023). "El aprendizaje automático revela la mecánica de control de la bisagra del ala de los insectos". BioRxiv: El servidor de preimpresiones para la biología . doi :10.1101/2023.06.29.547116. PMC 10327165. PMID 37425804. Consultado el 23 de agosto de 2023 .
- ^ abcdefghijk Wang, Z. Jane (2005). "Disección del vuelo de los insectos" (PDF) . Revisión anual de mecánica de fluidos . 37 (1): 183–210. Código Bibliográfico :2005AnRFM..37..183W. doi :10.1146/annurev.fluid.36.050802.121940.
- ^ abcdefg Sane, Sanjay P. (2003). "La aerodinámica del vuelo de los insectos" (PDF) . The Journal of Experimental Biology . 206 (23): 4191–4208. doi : 10.1242/jeb.00663 . PMID 14581590. S2CID 17453426.
- ^ Wagner, Herbert (1925). "Über die Entstehung des dynamischen Auftriebes von Tragflügeln" [Sobre el origen de la sustentación dinámica de los perfiles aerodinámicos]. Zeitschrift für Angewandte Mathematik und Mechanik (en alemán). 5 (1): 17–35. Código Bib : 1925ZaMM....5...17W. doi :10.1002/zamm.19250050103.
- ^ "Transición y turbulencia". Universidad de Princeton . Consultado el 8 de julio de 2021 .
- ^ Ellis, DG; Stollery, JL (1988). "El comportamiento y el rendimiento de los flaps de vórtice de borde de ataque" (PDF) . ICAS 1988 Jerusalén . 1988 . Consejo Internacional de Ciencias Aeronáuticas: 758–765 . Consultado el 8 de julio de 2021 .
- ^ Himmelskamp, H. (1945) "Investigaciones de perfil en una hélice rotatoria". Tesis doctoral, Universidad de Göttingen .
- ^ abcdefghijklmnopqrstu v Davidovits, Paul (2008). Física en biología y medicina. Academic Press . págs. 78-79. ISBN 978-0-12-369411-9.
- ^ Hope, Daniel K; DeLuca, Anthony M.; O'Hara, Ryan P (3 de enero de 2018). "Investigación sobre los efectos del número de Reynolds en un ala batiente biomimética". Revista internacional de microvehículos aéreos . 10 (1): 106–122. doi : 10.1177/1756829317745319 .
- ^ "Capturando la estela". Scientific American . 28 de junio de 1999.
- ^ Weis-Fogh, Torkel (1973). "Estimaciones rápidas de la aptitud para el vuelo en animales que planean, incluidos nuevos mecanismos de producción de sustentación". Journal of Experimental Biology . 59 : 169–230. doi :10.1242/jeb.59.1.169.
- ^ ab Santhanakrishnan, A.; Robinson, A.; Jones, S.; Low, A.; Gadi, S.; Hendrick, T.; Miller, L. (2014). "Mecanismo de aplauso y lanzamiento con alas porosas interactuantes en el vuelo de insectos diminutos". The Journal of Experimental Biology . 217 (Pt 21): 3898–4709. doi : 10.1242/jeb.084897 . PMID 25189374.
- ^ ab Kolomenskiy, D; Moffatt, H.; Farge, M.; Schneider, K. (2011). "Simulaciones numéricas bidimensionales y tridimensionales del aplauso-lanzamiento-barrido de insectos en vuelo". Journal of Fluids and Structures . 27 (5): 784. Bibcode :2011JFS....27..784K. doi :10.1016/j.jfluidstructs.2011.05.002.
- ^ Bennett, L. (1977). "Aerodinámica de aplausos y lanzamientos: una evaluación experimental". Revista de biología experimental . 69 : 261–272. doi :10.1242/jeb.69.1.261.
- ^ abc Miller, L.; Peskin, S. (2009). "Aplausos y lanzamientos flexibles en el vuelo de insectos diminutos". Revista de biología experimental . 212 (19): 3076–3090. doi : 10.1242/jeb.028662 . PMID 19749100. S2CID 29711043.
- ^ ab Lehmann, F.-O.; Sane, S.; Dickinson, M. (2005). "Los efectos aerodinámicos de la interacción ala-ala en el aleteo de las alas de los insectos". Journal of Experimental Biology . 208 (Pt 16): 3075–3092. doi : 10.1242/jeb.01744 . PMID 16081606. S2CID 7750411.
- ^ Lehmann, F.-O.; Pick, S. (2007). "El beneficio aerodinámico de la interacción ala-ala depende de la trayectoria del aleteo en los insectos". Journal of Experimental Biology . 210 (Pt 8): 1362–1377. doi : 10.1242/jeb.02746 . PMID 17401119. S2CID 23330782.
- ^ abcd Cheng, Xin; Sun, Mao (11 de mayo de 2016). "Medición de la cinemática del ala y aerodinámica en un pequeño insecto en vuelo estacionario". Scientific Reports . 6 (1): 25706. Bibcode :2016NatSR...625706C. doi :10.1038/srep25706. PMC 4863373 . PMID 27168523.
- ^ Kasoju, V.; Santhanakrishnan, A. (2021). "Interacción aerodinámica de pares de alas erizadas en vuelo". Física de fluidos . 33 (3): 031901. arXiv : 2011.00939 . Código Bibliográfico :2021PhFl...33c1901K. doi :10.1063/5.0036018. S2CID 226227261.
- ^ Weisberger, Mindy (19 de febrero de 2016). «¿Nadar como una mariposa? El caracol marino "vuela" por el agua». Scientific American . Consultado el 20 de febrero de 2016 .
- ^ Murphy, D.; Adhikari, D.; Webster, D.; Yen, J. (2016). "Vuelo submarino de la mariposa marina planctónica". Revista de biología experimental . 219 (4): 535–543. doi : 10.1242/jeb.129205 . PMID 26889002.
- ^ "Alas de insectos en general". Aerodinámica de insectos . Cislunar Aerospace. 1997. Consultado el 28 de marzo de 2011 .
- ^ "Mariposas de la familia Pieridae (blancas)". Bumblebee.org . Consultado el 18 de marzo de 2018 .
- ^ ab Dudley, Robert (2000). La biomecánica del vuelo de los insectos: forma, función, evolución . Princeton, Nueva Jersey: Princeton University Press . pág. 69. JSTOR j.ctv301g2x.
- ^ ab Stocks, Ian. (2008). Sección Acoplamiento de alas en capineras (Ed.) (2008) "Encyc. Entom.", vol. 4, pág. 4266
- ^ Scoble, Malcolm J. (1995). Los lepidópteros: forma, función y diversidad. Museo de Historia Natural . pp. 56–60. ISBN 978-0-19-854952-9.
- ^ ab Powell, Jerry A. Ch. Lepidoptera (págs. 631-664) en Resh y Cardé (Eds). "Enciclopedia de insectos". 2003.
- ^ Gorb, S. (2001) Cap. 4.1.5 "Entrelazamiento de partes del cuerpo". págs. 46-50.
- ^ Woiwod, IP; Reynolds, DR; Thomas, CD (Eds) 2001. Movimiento de insectos: mecanismos y consecuencias. CAB International.
- ^ Joos, B. (1987). "Uso de carbohidratos en los músculos de vuelo de Manduca sexta durante el calentamiento previo al vuelo". Journal of Experimental Biology . 133 : 317–327. doi :10.1242/jeb.133.1.317.
- ^ Sane, Sanjay P., Alexandre Dieudonné, Mark A. Willis y Thomas L. Daniel. "Los mecanosensores antenales median el control del vuelo en las polillas". Science 315, núm. 5813 (2007): 863-866.
- ^ Dickerson, Bradley H., Alysha M. de Souza, Ainul Huda y Michael H. Dickinson. "Las moscas regulan el movimiento de las alas mediante el control activo de un giroscopio de doble función". Current Biology 29, núm. 20 (2019): 3517-3524.
- ^ Wolf, Harald. "La langosta tegula: importancia para la generación del ritmo de vuelo, el control del movimiento de las alas y la producción de fuerza aerodinámica". Journal of Experimental Biology 182, no. 1 (1993): 229-253.
- ^ Misof, B.; Liu, S.; Meusemann, K.; Peters, RS; Donath, A.; et al. (2014). "La filogenómica resuelve el tiempo y el patrón de la evolución de los insectos". Science . 346 (6210): 763–767. Bibcode :2014Sci...346..763M. doi :10.1126/science.1257570. PMID 25378627. S2CID 36008925.
- ^ Brauckmann, Carsten; Schneider, Jörg (1996). "Ein unter-karbonisches Insekt aus dem Raum Bitterfeld/Delitzsch (Pterygota, Arnsbergium, Deutschland)" [Un insecto del Carbonífero Inferior del área de Bitterfeld/Delitzsch (Pterygota, Arnsbergian, Alemania)]. Neues Jahrbuch für Geologie und Paläontologie - Monatshefte (en alemán). 1996 (1): 17–30. doi :10.1127/njgpm/1996/1996/17.
- ^ Tillyard, RJ (2009). "Algunas observaciones sobre los insectos fósiles del Devónico de los yacimientos de sílex de Rhynie, Old Red Sandstone". Transactions of the Royal Entomological Society of London . 76 (1): 65–71. doi :10.1111/j.1365-2311.1928.tb01188.x.
- ^ Haug, Carolin; Haug, Joachim (2017). "El insecto volador más antiguo que se presume: ¿es más probable que sea un miriápodo?". PeerJ . 5 : e3402. doi : 10.7717/peerj.3402 . PMC 5452959 . PMID 28584727.
- ^ Wipfler, Benjamin; et al. (19 de febrero de 2019). "Historia evolutiva de los polineópteros y sus implicaciones para nuestra comprensión de los primeros insectos alados". Actas de la Academia Nacional de Ciencias . 116 (8): 3024–3029. Bibcode :2019PNAS..116.3024W. doi : 10.1073/pnas.1817794116 . PMC 6386694 . PMID 30642969.
- ^ Yanoviak, Stephen P.; Dudley, Robert (julio de 2018). "Saltos y comportamiento aéreo de larvas de efímeras acuáticas (Myobaetis ellenae, Baetidae)". Estructura y desarrollo de los artrópodos . 47 (4): 370–374. Bibcode :2018ArtSD..47..370Y. doi : 10.1016/j.asd.2017.06.005 . PMID 28684306. S2CID 205697025.
- ^ ab Trueman, JWH (1990), Comentario: evolución de las alas de los insectos: un modelo de extremidades extáticas más enditas. Revista Canadiense de Zoología .
- ^ ab Crampton, G. (1916). "El origen filogenético y la naturaleza de las alas de los insectos según la teoría paranotal". Revista de la Sociedad Entomológica de Nueva York . 24 (1): 1–39. JSTOR 25003692.
- ^ abc Grimaldi, David; Engel, Michael S. (2005). Los insectos surcan los cielos . Nueva York: Cambridge University Press . págs. 155–159.
{{cite book}}:|work=ignorado ( ayuda ) - ^ Müller, Fritz (1875) Jena. Zeitung Naturwissenschaften , 9, 241.
- ^ Kukalova-Peck, Jarmila (1978). "Origen y evolución de las alas de los insectos y su relación con la metamorfosis, tal como se documenta en el registro fósil". Revista de morfología . 156 (1). Wiley: 53–125. doi :10.1002/jmor.1051560104. PMID 30231597. S2CID 52301138.
- ^ Rasnitsyn, Alexander P. (1981). "Una teoría paranotal modificada del origen de las alas de los insectos". Journal of Morphology . 168 (3): 331–338. doi :10.1002/jmor.1051680309. PMID 30110990. S2CID 52010764.
- ^ Thomas, Adrian LR ; Norberg, R. Åke (1996). "Rozando la superficie: ¿el origen del vuelo en los insectos?". Tendencias en ecología y evolución . 11 (5): 187–188. Bibcode :1996TEcoE..11..187T. doi :10.1016/0169-5347(96)30022-0. PMID 21237803.
- ^ Marden, James (2003). "La hipótesis del roce de la superficie para la evolución del vuelo de los insectos". Acta Zoologica Cracoviensia . 46 : 73–84.
- ^ Yanoviak, Stephen P.; Kaspari, M.; Dudley, R. (2009). "Hexápodos planeadores y los orígenes del comportamiento aéreo de los insectos". Biology Letters . 5 (4): 510–2. doi :10.1098/rsbl.2009.0029. PMC 2781901 . PMID 19324632.
- ^ Averof, Michalis; Cohen, Stephen M. (1997). "Origen evolutivo de las alas de los insectos a partir de branquias ancestrales". Nature . 385 (6617). Springer Science and Business Media: 627–630. Bibcode :1997Natur.385..627A. doi :10.1038/385627a0. PMID 9024659. S2CID 4257270.
- ^ Niwa, Nao; Akimoto-Kato, Ai; Niimi, Teruyuki; Tojo, Koji; Machida, Ryuichiro; Hayashi, Shigeo (17 de marzo de 2010). "Origen evolutivo del ala de los insectos a través de la integración de dos módulos de desarrollo". Evolution & Development . 12 (2): 168–176. doi :10.1111/j.1525-142x.2010.00402.x. PMID 20433457. S2CID 15838166.
- ^ Elias-Neto, Moysés; Belles, Xavier (2016). "Las estructuras tergales y pleurales contribuyen a la formación de alas protorácicas ectópicas en cucarachas". Royal Society Open Science . 3 (8). The Royal Society: 160347. Bibcode :2016RSOS....360347E. doi :10.1098/rsos.160347. PMC 5108966 . PMID 27853616.
- ^ Tomoyasu, Yoshinori; Ohde, Takahiro; Clark-Hachtel, Courtney (14 de marzo de 2017). "Lo que los homólogos seriales pueden decirnos sobre el origen de las alas de los insectos". F1000Research . 6 : 268. doi : 10.12688/f1000research.10285.1 . PMC 5357031 . PMID 28357056.
- ^ Prokop, Jakub; Pecharová, Martina; Nel, André; Hörnschemeyer, Thomas; Krzemińska, Ewa; Krzemiński, Wiesław; Engel, Michael S. (2017). "Las almohadillas de las alas de ninfa paleozoica apoyan el modelo dual de los orígenes de las alas de los insectos". Biología actual . 27 (2): 263–269. Código Bib : 2017CBio...27..263P. doi : 10.1016/j.cub.2016.11.021 . PMID 28089512.
Lectura adicional
- Dickinson, MH; Lehmann, FO; Sane, SP (1999). "Rotación de alas y base aerodinámica del vuelo de los insectos". Science . 284 (5422): 1954–60. doi :10.1126/science.284.5422.1954. PMID 10373107.
- Ellington, Charles P.; Van Den Berg, Coen; Willmott, Alexander P.; Thomas, Adrian LR (1996). "Vórtices de vanguardia en el vuelo de los insectos". Nature . 384 (6610): 626–630. Bibcode :1996Natur.384..626E. doi :10.1038/384626a0. S2CID 4358428.
- Ellington, CP (1984). "La aerodinámica del vuelo de los insectos en suspensión. I. El análisis cuasi-estacionario". Philosophical Transactions of the Royal Society B : Biological Sciences . 305 (1122): 1–15. Bibcode :1984RSPTB.305....1E. doi :10.1098/rstb.1984.0049.
- Ellington, CP (1999). "La nueva aerodinámica del vuelo de los insectos: aplicaciones a los microvehículos aéreos". The Journal of Experimental Biology . 202 (Pt 23): 3439–3448. doi :10.1242/jeb.202.23.3439. PMID 10562527.
- Lewin, GC; Haj-Hariri, H. (2003). "Modelado de la generación de empuje de un perfil aerodinámico bidimensional en un flujo viscoso". Journal of Fluid Mechanics . 492 : 339–362. Bibcode :2003JFM...492..339L. doi :10.1017/S0022112003005743. S2CID 122077834.
- Pringle, JWS (1975). Vuelo de insectos . Oxford Biology Readers. Vol. 52.
- Sane, SP (2003). "La aerodinámica del vuelo de los insectos". Revista de biología experimental . 206 (parte 23): 4191–208. doi :10.1242/jeb.00663. PMID 14581590. S2CID 17453426.
- Savage, SB; Newman, BG; Wong, DTM (1979). "El papel de los vórtices y los efectos inestables durante el vuelo estacionario de las libélulas". The Journal of Experimental Biology . 83 (1): 59–77. doi :10.1242/jeb.83.1.59.
- Smyth, T. Jr. (1985). "Sistemas musculares". En Blum, MS Blum (ed.). Fundamentos de la fisiología de los insectos . John Wiley and Sons . págs. 227–286.
- Sotavalta, O. (1953). "Registros de alta frecuencia de aleteo y vibración torácica en algunos mosquitos". Boletín biológico de Woods Hole . 104 (3): 439–444. doi :10.2307/1538496. JSTOR 1538496.
- Van Den Berg, C.; Ellington, CP (1997). "La estela de vórtice de un modelo de polilla halcón 'flotante'". Philosophical Transactions of the Royal Society B . 352 (1351): 317–328. Bibcode :1997RSPTB.352..317V. doi :10.1098/rstb.1997.0023. PMC 1691928 .
- Walker, JA (septiembre de 2002). "Elevación rotacional: ¿algo diferente o más de lo mismo?". The Journal of Experimental Biology . 205 (Pt 24): 3783–3792. doi :10.1242/jeb.205.24.3783. PMID 12432002.
- Zbikowski, R. (2002). "Sobre el modelado aerodinámico de un ala batiente similar a la de un insecto en vuelo estacionario para microvehículos aéreos". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences . 360 (1791): 273–290. Bibcode :2002RSPTA.360..273Z. doi :10.1098/rsta.2001.0930. PMID 16210181. S2CID 2430367.
Enlaces externos
- El papel de un insecto en el desarrollo de microvehículos aéreos
- Microvehículos aéreos con alas batientes similares a insectos
- La novedosa aerodinámica del vuelo de los insectos: aplicaciones a los microvehículos aéreos
- La aerodinámica del vuelo de los insectos
- Músculos del vuelo Archivado el 22 de agosto de 2004 en Wayback Machine.
- Visualización del flujo de los mecanismos aerodinámicos de la mariposa
- El vuelo del abejorro
- Vuelo de insectos