Altura de la escala
En las ciencias atmosféricas , de la tierra y planetarias , una altura de escala , usualmente denotada por la letra mayúscula H , es una distancia ( vertical o radial ) sobre la cual una cantidad física disminuye por un factor de e (la base de los logaritmos naturales , aproximadamente 2,718).
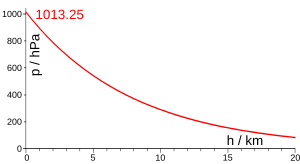
Altura de escala utilizada en un modelo simple de presión atmosférica
En el caso de las atmósferas planetarias, la altura de escala es el aumento de altitud para el cual la presión atmosférica disminuye en un factor e . La altura de escala permanece constante para una temperatura particular. Puede calcularse mediante [1] [2]
o equivalentemente donde:
- k B = constante de Boltzmann =1.381 × 10 −23 J⋅K −1 [ 3]
- R = constante molar del gas
- T = temperatura atmosférica media en kelvin = 250 K [4] para la Tierra
- m = masa media de una molécula
- M = masa molar media de partículas atmosféricas = 0,029 kg/mol para la Tierra
- g = aceleración debida a la gravedad en la ubicación actual
La presión (fuerza por unidad de área) a una altitud dada es el resultado del peso de la atmósfera suprayacente. Si a una altura z la atmósfera tiene una densidad ρ y una presión P , entonces al ascender una altura infinitesimalmente pequeña dz la presión disminuirá en una cantidad dP , igual al peso de una capa de atmósfera de espesor dz .
Por lo tanto: donde g es la aceleración debida a la gravedad. Para dz pequeño es posible suponer que g es constante; el signo menos indica que a medida que aumenta la altura, la presión disminuye. Por lo tanto, utilizando la ecuación de estado para un gas ideal de masa molecular media M a temperatura T , la densidad se puede expresar como
Combinando estas ecuaciones se obtiene que luego se puede incorporar con la ecuación para H dada anteriormente para obtener: que no cambiará a menos que lo haga la temperatura. Integrando lo anterior y suponiendo que P 0 es la presión a la altura z = 0 (presión al nivel del mar ), la presión a la altura z se puede escribir como:
Esto se traduce como que la presión disminuye exponencialmente con la altura. [5]
En la atmósfera de la Tierra , la presión a nivel del mar P 0 promedia aproximadamente1,01 × 10 5 Pa , la masa molecular media del aire seco es28,964 Da y por lo tanto m =28.964 Da ×1,660 × 10 −27 kg/Da =4,808 × 10 −26 kg . En función de la temperatura, la altura de escala de la atmósfera terrestre es, por tanto, H / T = k / mg =1.381 × 10 −23 J⋅K −1 / (4,808 × 10 −26 kg ×9,81 m⋅s −2 ) =29,28 m/K . Esto produce las siguientes alturas de escala para temperaturas del aire representativas.
- Temperatura = 290 K, Altitud = 8500 m
- Temperatura = 273 K, Altitud = 8000 m
- Temperatura = 260 K, Altitud = 7610 m
- Temperatura = 210 K, Altitud = 6000 m
Estas cifras deben compararse con la temperatura y la densidad de la atmósfera de la Tierra representadas en NRLMSISE-00 , que muestra que la densidad del aire cae de 1200 g/m 3 a nivel del mar a 0,125 g/m 3 a 70 km, un factor de 9600, lo que indica una altura de escala promedio de 70 / ln(9600) = 7,64 km, consistente con la temperatura media del aire indicada en ese rango de cerca de 260 K.
Nota:
- La densidad está relacionada con la presión por las leyes de los gases ideales . Por lo tanto, la densidad también disminuirá exponencialmente con la altura a partir de un valor de ρ 0 a nivel del mar aproximadamente igual a1,2 kg⋅m −3 .
- A una altitud superior a 100 km, la atmósfera ya no está bien mezclada y cada especie química tiene su propia escala de altura.
- Aquí se supuso que la temperatura y la aceleración gravitacional eran constantes, pero ambas pueden variar en grandes distancias.
Ejemplos planetarios
Alturas aproximadas a escala atmosférica para cuerpos seleccionados del Sistema Solar:
Altura de escala para un disco delgado

Para un disco de gas alrededor de un objeto central condensado, como, por ejemplo, una protoestrella, se puede derivar una altura de escala del disco que es algo análoga a la altura de escala planetaria. Comenzamos con un disco de gas que tiene una masa que es pequeña en relación con el objeto central. Suponemos que el disco está en equilibrio hidrostático con el componente z de la gravedad de la estrella, donde el componente de gravedad apunta al plano medio del disco: donde:
- G = Constante gravitacional ≈6,674 × 10 −11 m 3 ⋅ kg −1 ⋅ s −2 [ 15]
- r = la coordenada cilíndrica radial para la distancia desde el centro de la estrella o del objeto centralmente condensado
- z = la coordenada cilíndrica de altura/altitud para la distancia desde el plano medio del disco (o centro de la estrella)
- M * = la masa de la estrella/objeto centralmente condensado
- P = la presión del gas en el disco
- = la densidad de masa del gas en el disco
En la aproximación del disco delgado, la ecuación de equilibrio hidrostático es
Para determinar la presión del gas, se puede utilizar la ley de los gases ideales : con:
- T = la temperatura del gas en el disco, donde la temperatura es una función de r , pero independiente de z
- = la masa molecular media del gas
Usando la ley de los gases ideales y la ecuación de equilibrio hidrostático, se obtiene: que tiene como solución donde es la densidad de masa del gas en el plano medio del disco a una distancia r del centro de la estrella y es la altura de escala del disco con la masa solar , la unidad astronómica y la unidad de masa atómica .
Como aproximación ilustrativa, si ignoramos la variación radial de la temperatura, , vemos que y que el disco aumenta en altitud a medida que uno se aleja radialmente del objeto central.
Debido al supuesto de que la temperatura del gas en el disco, T , es independiente de z , a veces se conoce como la altura de escala del disco isotérmico.
Altura de la escala del disco en un campo magnético
Un campo magnético en un disco de gas delgado alrededor de un objeto central puede cambiar la altura de escala del disco. [16] [17] [18] Por ejemplo, si un disco no perfectamente conductor está girando a través de un campo magnético poloidal (es decir, el campo magnético inicial es perpendicular al plano del disco), entonces se producirá un campo magnético toroidal (es decir, paralelo al plano del disco) dentro del disco, que apretará y comprimirá el disco. En este caso, la densidad del gas del disco es: [18]
donde la densidad de corte tiene la forma donde
- es la permeabilidad del espacio libre
- es la conductividad eléctrica del disco
- es la densidad de flujo magnético del campo poloidal en la dirección
- es la velocidad angular rotacional del objeto central (si el campo magnético poloidal es independiente del objeto central, entonces se puede establecer en cero)
- es la velocidad angular kepleriana del disco a una distancia del objeto central.
Estas fórmulas dan la altura máxima, , del disco magnetizado mientras que la altura de la escala magnética de plegado electrónico, , es
Véase también
Referencias
- ^ "Glosario de meteorología - altura de escala". Sociedad Meteorológica Americana (AMS).
- ^ "Altura de la escala de presión". Wolfram Research .
- ^ "Valor CODATA 2022: constante de Boltzmann". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
- ^ "Daniel J. Jacob: "Introducción a la química atmosférica", Princeton University Press, 1999". Archivado desde el original el 10 de abril de 2013. Consultado el 18 de abril de 2013 .
- ^ "Ejemplo: La altura de escala de la atmósfera terrestre" (PDF) . Archivado desde el original (PDF) el 16 de julio de 2011.
- ^ "Hoja informativa sobre Venus". NASA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre la Tierra". NASA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Marte". NASA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Júpiter". NASA. Archivado desde el original el 13 de octubre de 2011. Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Saturno". NASA. Archivado desde el original el 18 de agosto de 2011. Consultado el 28 de septiembre de 2013 .
- ^ Justus, CG; Aleta Duvall; Vernon W. Keller (1 de agosto de 2003). "Engineering-Level Model Atmospheres For Titan and Mars". Taller internacional sobre análisis y ciencia de trayectorias atmosféricas de entrada y descenso de sondas planetarias, Lisboa, Portugal, 6-9 de octubre de 2003, Actas: ESA SP-544 . ESA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Urano". NASA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Neptuno". NASA . Consultado el 28 de septiembre de 2013 .
- ^ "Hoja informativa sobre Plutón". NASA . Consultado el 28 de septiembre de 2020 .
- ^ "Valor CODATA 2022: constante de gravitación newtoniana". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
- ^ Lovelace, RVE; Mehanian, C.; Mobarry, CM; Sulkanen, ME (septiembre de 1986). "Teoría de flujos magnetohidrodinámicos axisimétricos: discos". Suplemento de la revista Astrophysical Journal . 62 : 1. Bibcode :1986ApJS...62....1L. doi : 10.1086/191132 . Consultado el 26 de enero de 2022 .
- ^ Campbell, CG; Heptinstall, PM (agosto de 1998). "Estructura del disco alrededor de acretores fuertemente magnéticos: una solución de disco completo con difusividad turbulenta". Monthly Notices of the Royal Astronomical Society . 299 (1): 31. Bibcode :1998MNRAS.299...31C. doi : 10.1046/j.1365-8711.1998.01576.x .
- ^ ab Liffman, Kurt; Bardou, Anne (octubre de 1999). "Una escala magnética: el efecto de los campos magnéticos toroidales en el espesor de los discos de acreción". Monthly Notices of the Royal Astronomical Society . 309 (2): 443. Bibcode :1999MNRAS.309..443L. doi : 10.1046/j.1365-8711.1999.02852.x .























![{\displaystyle \rho (r,z)=\rho _{0}(r)\exp \left(-\left({\frac {z}{h_{D}}}\right)^{2}\right)-\rho _{\text{corte}}(r)\left[1-\exp \left(-\left({\frac {z}{h_{D}}}\right)^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eae0fe3f516452dae19437709fc39ffcc6c76b3)












