Ápside
Este artículo necesita citas adicionales para su verificación . ( diciembre de 2020 ) |
Un ábside (del griego antiguo ἁψίς ( hapsís ) 'arco, bóveda'; pl. ábsides / ˈæ p s ɪ ˌ d iː z / AP -sih-deez ) [1] [2] es el punto más lejano o más cercano en la órbita de un cuerpo planetario alrededor de su cuerpo primario . La línea de ábsides (también llamada apogeo) es la línea que conecta los dos valores extremos .
Los ábsides pertenecientes a órbitas alrededor del Sol tienen nombres distintos para diferenciarse de otros ábsides; estos nombres son afelio para el punto más lejano y perihelio para el punto más cercano en la órbita solar. [3] Los dos ábsides de la Luna son el punto más lejano, apogeo , y el punto más cercano, perigeo , de su órbita alrededor de la Tierra anfitriona . Los dos ábsides de la Tierra son el punto más lejano, afelio , y el punto más cercano, perihelio , de su órbita alrededor del Sol anfitrión. Los términos afelio y perihelio se aplican de la misma manera a las órbitas de Júpiter y los otros planetas , los cometas y los asteroides del Sistema Solar .
| Parte de una serie sobre |
| Astrodinámica |
|---|
Descripción general

∗Periapsis y apoapsis como distancias: las distancias más pequeña y más grande entre el orbitador y su cuerpo anfitrión.
En cualquier órbita elíptica hay dos ábsides . El nombre de cada ábside se crea a partir de los prefijos ap- , apo- (de ἀπ(ό) , (ap(o)-) 'lejos de') para el más lejano o peri- (de περί (peri-) 'cerca') para el punto más cercano al cuerpo primario , con un sufijo que describe el cuerpo primario. El sufijo para la Tierra es -gee , por lo que los nombres de los ábsides son apogeo y perigeo . Para el Sol, el sufijo es -helion , por lo que los nombres son afelio y perihelio .
Según las leyes de movimiento de Newton , todas las órbitas periódicas son elipses. El baricentro de los dos cuerpos puede estar perfectamente dentro del cuerpo más grande (por ejemplo, el baricentro Tierra-Luna está aproximadamente a un 75 % del camino desde el centro de la Tierra hasta su superficie). [4] Si, en comparación con la masa más grande, la masa más pequeña es despreciable (por ejemplo, para los satélites), entonces los parámetros orbitales son independientes de la masa más pequeña.
Cuando se utiliza como sufijo (es decir, -apsis ), el término puede referirse a las dos distancias desde el cuerpo primario hasta el cuerpo en órbita cuando este último se encuentra: 1) en el punto de periapsis , o 2) en el punto de apoapsis (compárense ambos gráficos, segunda figura). La línea de ápsides denota la distancia de la línea que une los puntos más cercanos y más lejanos a través de una órbita; también se refiere simplemente al rango extremo de un objeto que orbita alrededor de un cuerpo anfitrión (ver figura superior; ver tercera figura).
En mecánica orbital , los ábsides se refieren técnicamente a la distancia medida entre el baricentro del sistema de dos cuerpos y el centro de masa del cuerpo en órbita. Sin embargo, en el caso de una nave espacial , los términos se usan comúnmente para referirse a la altitud orbital de la nave espacial sobre la superficie del cuerpo central (asumiendo un radio de referencia estándar constante).

Terminología
A menudo se utilizan las palabras "pericentro" y "apocentro", aunque en el uso técnico se prefiere periapsis/apoapsis.
- Para situaciones genéricas donde no se especifica el primario, se utilizan los términos pericentro y apocentro para nombrar los puntos extremos de las órbitas (ver tabla, figura superior); periapsis y apoapsis (o apapsis ) son alternativas equivalentes, pero estos términos también se refieren con frecuencia a distancias, es decir, las distancias más pequeñas y más grandes entre el orbitador y su cuerpo anfitrión (ver segunda figura).
- Para un cuerpo que orbita alrededor del Sol , el punto de menor distancia es el perihelio ( / ˌ p ɛr ɪ ˈ h iː l i ə n / ), y el punto de mayor distancia es el afelio ( / æ p ˈ h iː l i ə n / ) ; [5] cuando se habla de órbitas alrededor de otras estrellas, los términos se convierten en periastrón y apastrón .
- Cuando se habla de un satélite de la Tierra , incluida la Luna , el punto de menor distancia es el perigeo ( / ˈp ɛr ɪ dʒ iː / ), y el de mayor distancia, el apogeo (del griego antiguo : Γῆ ( Gē ), "tierra" o "tierra"). [6]
- Para los objetos en órbita lunar , el punto de menor distancia se llama pericinthion ( / ˌ p ɛr ɪ ˈ s ɪ n θ i ə n / ) y la distancia mayor, apocynthion ( / ˌ æ p ə ˈ s ɪ n θ i ə n / ). También se utilizan los términos periluno y apoluno , así como periseleno y aposeleno . [7] Dado que la Luna no tiene satélites naturales, esto solo se aplica a los objetos creados por el hombre.
Etimología
Las palabras perihelio y afelio fueron acuñadas por Johannes Kepler [8] para describir los movimientos orbitales de los planetas alrededor del Sol. Las palabras se forman a partir de los prefijos peri- (griego: περί , cerca) y apo- (griego: ἀπό , lejos de), añadidos a la palabra griega para el Sol, ( ἥλιος , o hēlíos ). [5]
Se utilizan varios términos relacionados para otros objetos celestes . Los sufijos -gee , -helion , -astron y -galacticon se utilizan con frecuencia en la literatura astronómica para referirse a la Tierra, el Sol, las estrellas y el centro galáctico respectivamente. El sufijo -jove se utiliza ocasionalmente para Júpiter, pero -saturnium se ha utilizado muy raramente en los últimos 50 años para Saturno. La forma -gee también se utiliza como un término genérico de aproximación más cercana a "cualquier planeta", en lugar de aplicarse solo a la Tierra.
Durante el programa Apolo , se utilizaron los términos pericynthion y apocynthion para referirse a la órbita de la Luna ; hacen referencia a Cynthia, un nombre alternativo para la diosa griega de la Luna, Artemisa . [9] Más recientemente, durante el programa Artemisa , se han utilizado los términos perilune y apolune . [10]
En relación con los agujeros negros, el término peribotron fue utilizado por primera vez en un artículo de 1976 de J. Frank y MJ Rees, [11] quienes atribuyen a WR Stoeger la sugerencia de crear un término utilizando la palabra griega para pozo: "bothron".
Los términos perimelasma y apomelasma (de una raíz griega) fueron utilizados por el físico y autor de ciencia ficción Geoffrey A. Landis en una historia publicada en 1998, [12] apareciendo así antes de perinigricon y aponigricon (del latín) en la literatura científica en 2002. [13]
Resumen de terminología
Los sufijos que se muestran a continuación pueden añadirse a los prefijos peri- o apo- para formar nombres únicos de ápsides para los cuerpos en órbita del sistema anfitrión/ (primario) indicado . Sin embargo, solo para los sistemas Tierra, Luna y Sol se utilizan comúnmente los sufijos únicos. Los estudios de exoplanetas suelen utilizar -astron , pero por lo general, para otros sistemas anfitriones se utiliza en su lugar el sufijo genérico, -apsis . [14] [ verificación fallida ]
Objeto anfitrión astronómico | Sufijo | Origen del nombre |
|---|---|---|
| Sol | -helio | Helios |
| Mercurio | -hermión | Hermes |
| Venus | -guadaña | Citereo |
| Tierra | -Caramba | Gea |
| Luna | -luna [7] -cinthion -selene [7] | Luna Cynthia Selene |
| Marte | -areión | Ares |
| Ceres | -demeter [15] | Deméter |
| Júpiter | -Júpiter | Zeus Júpiter |
| Saturno | -chron [7] -kronos -saturnio -corona [16] | Cronos Saturn |
| Urano | -uranión | Urano |
| Neptuno | -poseideo [17] -poseidón | Poseidón |
Objeto anfitrión astronómico | Sufijo | Origen del nombre |
|---|---|---|
| Estrella | -astron | Lat: astra ; estrellas |
| Galaxia | -galacticon | Gr: galaxias; galaxia |
| Baricentro | -centro -foco -ápside | |
| Agujero negro | -melasma -bothron -nigricon | Gr: melos; negro Gr: bothros ; agujero Lat: niger ; negro |
Perihelio y afelio

El perihelio (q) y el afelio (Q) son los puntos más cercanos y más lejanos respectivamente de la órbita directa de un cuerpo alrededor del Sol .
La comparación de los elementos osculadores en una época específica con los de una época diferente generará diferencias. El tiempo de paso por el perihelio como uno de los seis elementos osculadores no es una predicción exacta (salvo para un modelo genérico de dos cuerpos ) de la distancia mínima real al Sol utilizando el modelo dinámico completo . Las predicciones precisas del paso por el perihelio requieren integración numérica .
Planetas interiores y planetas exteriores
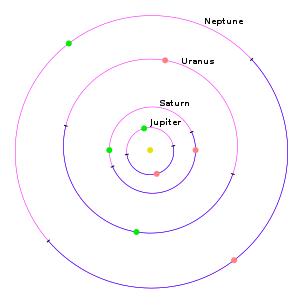
Las dos imágenes siguientes muestran las órbitas, los nodos orbitales y las posiciones del perihelio (q) y el afelio (Q) de los planetas del Sistema Solar [18] vistos desde arriba del polo norte del plano eclíptico de la Tierra , que es coplanar con el plano orbital de la Tierra . Los planetas viajan en sentido antihorario alrededor del Sol y, para cada planeta, la parte azul de su órbita viaja al norte del plano eclíptico, la parte rosa viaja al sur y los puntos marcan el perihelio (verde) y el afelio (naranja).
La primera imagen (abajo a la izquierda) muestra los planetas interiores , situados más allá del Sol, como Mercurio, Venus, la Tierra y Marte. La órbita terrestre de referencia está coloreada en amarillo y representa el plano orbital de referencia . En el momento del equinoccio de primavera, la Tierra se encuentra en la parte inferior de la figura. La segunda imagen (abajo a la derecha) muestra los planetas exteriores , que son Júpiter, Saturno, Urano y Neptuno.
Los nodos orbitales son los dos puntos finales de la "línea de nodos" donde la órbita inclinada de un planeta intersecta el plano de referencia; [19] aquí pueden "verse" como los puntos donde la sección azul de una órbita se encuentra con la rosa.
- Los puntos del perihelio (verde) y del afelio (naranja) de los planetas interiores del Sistema Solar
- Los puntos del perihelio (verde) y del afelio (naranja) de los planetas exteriores del Sistema Solar
Líneas de ábsides
El gráfico muestra el rango extremo (desde el punto de aproximación más cercano (perihelio) hasta el punto más lejano (afelio)) de varios cuerpos celestes en órbita alrededor del Sistema Solar : los planetas, los planetas enanos conocidos, incluido Ceres , y el cometa Halley . La longitud de las barras horizontales corresponde al rango extremo de la órbita del cuerpo indicado alrededor del Sol. Estas distancias extremas (entre el perihelio y el afelio) son las líneas de ábsides de las órbitas de varios objetos alrededor de un cuerpo anfitrión.

Distancias de cuerpos seleccionados del Sistema Solar al Sol. Los bordes izquierdo y derecho de cada barra corresponden al perihelio y al afelio del cuerpo, respectivamente, por lo que las barras largas denotan una excentricidad orbital alta . El radio del Sol es de 0,7 millones de km y el radio de Júpiter (el planeta más grande) es de 0,07 millones de km, ambos demasiado pequeños para resolverse en esta imagen.
Perihelio y afelio de la Tierra
Actualmente, la Tierra alcanza el perihelio a principios de enero, aproximadamente 14 días después del solsticio de diciembre . En el perihelio, el centro de la Tierra se encuentra aproximadamente0,983 29 unidades astronómicas (UA) o 147.098.070 km (91.402.500 mi) desde el centro del Sol. En contraste, la Tierra alcanza el afelio actualmente a principios de julio, aproximadamente 14 días después del solsticio de junio . La distancia del afelio entre los centros de la Tierra y el Sol es actualmente de aproximadamente1.016 71 AU o 152.097.700 km (94.509.100 mi).
Las fechas del perihelio y del afelio cambian con el tiempo debido a la precesión y otros factores orbitales, que siguen patrones cíclicos conocidos como ciclos de Milankovitch . A corto plazo, dichas fechas pueden variar hasta 2 días de un año a otro. [20] Esta variación significativa se debe a la presencia de la Luna: mientras que el baricentro Tierra-Luna se mueve en una órbita estable alrededor del Sol, la posición del centro de la Tierra, que está en promedio a unos 4.700 kilómetros (2.900 millas) del baricentro, podría desplazarse en cualquier dirección con respecto a él, y esto afecta el momento del acercamiento real más cercano entre los centros del Sol y la Tierra (que a su vez define el momento del perihelio en un año determinado). [21]
Debido a la mayor distancia en el afelio, solo el 93,55% de la radiación del Sol cae sobre un área dada de la superficie de la Tierra como lo hace en el perihelio, pero esto no explica las estaciones , que resultan en cambio de la inclinación del eje de la Tierra de 23,4° con respecto a la perpendicular al plano de la órbita terrestre. [22] De hecho, tanto en el perihelio como en el afelio es verano en un hemisferio mientras que es invierno en el otro. El invierno cae en el hemisferio donde la luz solar llega menos directamente, y el verano cae donde la luz solar llega más directamente, independientemente de la distancia de la Tierra al Sol.
En el hemisferio norte, el verano coincide con el afelio, cuando la radiación solar es más baja. A pesar de ello, los veranos en el hemisferio norte son, en promedio, 2,3 °C (4 °F) más cálidos que en el hemisferio sur, porque el hemisferio norte contiene mayores masas de tierra, que son más fáciles de calentar que los mares. [23]
Sin embargo, el perihelio y el afelio tienen un efecto indirecto sobre las estaciones: como la velocidad orbital de la Tierra es mínima en el afelio y máxima en el perihelio, el planeta tarda más en orbitar desde el solsticio de junio hasta el equinoccio de septiembre que desde el solsticio de diciembre hasta el equinoccio de marzo. Por lo tanto, el verano en el hemisferio norte dura un poco más (93 días) que el verano en el hemisferio sur (89 días). [24]
Los astrónomos suelen expresar el momento del perihelio en relación con el Primer Punto de Aries no en términos de días y horas, sino como un ángulo de desplazamiento orbital, la llamada longitud del periapsis (también llamada longitud del pericentro). Para la órbita de la Tierra, esto se llama longitud del perihelio , y en 2000 era de aproximadamente 282,895°; para 2010, había avanzado una pequeña fracción de grado a aproximadamente 283,067°, [25] es decir, un aumento medio de 62" por año.
En el caso de la órbita de la Tierra alrededor del Sol, el tiempo de ábside se expresa a menudo en términos de tiempo relativo a las estaciones, ya que esto determina la contribución de la órbita elíptica a las variaciones estacionales. La variación de las estaciones está controlada principalmente por el ciclo anual del ángulo de elevación del Sol, que es el resultado de la inclinación del eje de la Tierra medido desde el plano de la eclíptica . La excentricidad de la Tierra y otros elementos orbitales no son constantes, sino que varían lentamente debido a los efectos perturbadores de los planetas y otros objetos del sistema solar (ciclos de Milankovitch).
En una escala temporal muy larga, las fechas del perihelio y del afelio progresan a lo largo de las estaciones y forman un ciclo completo en 22.000 a 26.000 años. Existe un movimiento correspondiente de la posición de las estrellas vistas desde la Tierra, llamado precesión absidal (está estrechamente relacionada con la precesión de los ejes ). Las fechas y horas de los perihelios y afelios de varios años pasados y futuros se enumeran en la siguiente tabla: [26]
| Año | Perihelio | Afelio | ||
|---|---|---|---|---|
| Fecha | Hora ( UT ) | Fecha | Hora ( UT ) | |
| 2010 | 3 de enero | 00:09 | 6 de julio | 11:30 |
| 2011 | 3 de enero | 18:32 | 4 de julio | 14:54 |
| 2012 | 5 de enero | 00:32 | 5 de julio | 03:32 |
| 2013 | 2 de enero | 04:38 | 5 de julio | 14:44 |
| 2014 | 4 de enero | 11:59 | 4 de julio | 00:13 |
| 2015 | 4 de enero | 06:36 | 6 de julio | 19:40 |
| 2016 | 2 de enero | 22:49 | 4 de julio | 16:24 |
| 2017 | 4 de enero | 14:18 | 3 de julio | 20:11 |
| 2018 | 3 de enero | 05:35 | 6 de julio | 16:47 |
| 2019 | 3 de enero | 05:20 | 4 de julio | 22:11 |
| 2020 | 5 de enero | 07:48 | 4 de julio | 11:35 |
| 2021 | 2 de enero | 13:51 | 5 de julio | 22:27 |
| 2022 | 4 de enero | 06:55 | 4 de julio | 07:11 |
| 2023 | 4 de enero | 16:17 | 6 de julio | 20:07 |
| 2024 | 3 de enero | 00:39 | 5 de julio | 05:06 |
| 2025 | 4 de enero | 13:28 | 3 de julio | 19:55 |
| 2026 | 3 de enero | 17:16 | 6 de julio | 17:31 |
| 2027 | 3 de enero | 02:33 | 5 de julio | 05:06 |
| 2028 | 5 de enero | 12:28 | 3 de julio | 22:18 |
| 2029 | 2 de enero | 18:13 | 6 de julio | 05:12 |
Otros planetas
La siguiente tabla muestra las distancias de los planetas y planetas enanos al Sol en su perihelio y afelio. [27]
| Tipo de cuerpo | Cuerpo | Distancia del Sol en el perihelio | Distancia del Sol en el afelio | diferencia (%) | diferencia de insolación (%) |
|---|---|---|---|---|---|
| Planeta | Mercurio | 46.001.009 kilómetros (28.583.702 millas) | 69.817.445 kilómetros (43.382.549 millas) | 34% | 57% |
| Venus | 107.476.170 kilómetros (66.782.600 millas) | 108.942.780 kilómetros (67.693.910 millas) | 1,3% | 2,8% | |
| Tierra | 147.098.291 kilómetros (91.402.640 millas) | 152.098.233 kilómetros (94.509.460 millas) | 3,3% | 6,5% | |
| Marte | 206.655.215 kilómetros (128.409.597 millas) | 249.232.432 kilómetros (154.865.853 millas) | 17% | 31% | |
| Júpiter | 740.679.835 kilómetros (460.237.112 millas) | 816.001.807 kilómetros (507.040.016 millas) | 9,2% | 18% | |
| Saturno | 1.349.823.615 kilómetros (838.741.509 millas) | 1.503.509.229 kilómetros (934.237.322 millas) | 10% | 19% | |
| Urano | 2.734.998.229 km (1,699449110 × 10 9 millas) | 3.006.318.143 km (1,868039489 × 10 9 millas) | 9.0% | 17% | |
| Neptuno | 4.459.753.056 km (2,771162073 × 10 9 millas) | 4.537.039.826 km (2,819185846 × 10 9 millas) | 1,7% | 3,4% | |
| Planeta enano | Ceres | 380.951.528 kilómetros (236.712.305 millas) | 446.428.973 kilómetros (277.398.103 millas) | 15% | 27% |
| Plutón | 4.436.756.954 km (2,756872958 × 10 9 millas) | 7.376.124.302 kilometros (4,583311152 × 10 9 millas) | 40% | 64% | |
| Haumea | 5.157.623.774 km (3,204798834 × 10 9 millas) | 7.706.399.149 km (4,788534427 × 10 9 millas) | 33% | 55% | |
| Hacerhacer | 5.671.928.586 km (3,524373028 × 10 9 millas) | 7.894.762.625 km (4,905578065 × 10 9 millas) | 28% | 48% | |
| Eris | 5.765.732.799 km (3,582660263 × 10 9 millas) | 14.594.512.904 km (9,068609883 × 10 9 millas) | 60% | 84% |
Fórmulas matemáticas
Estas fórmulas caracterizan el pericentro y el apocentro de una órbita:
- Pericentro
- Velocidad máxima, , a la distancia mínima (pericentro), .
- Apocentro
- Velocidad mínima, , a la distancia máxima (apocentro), .
Mientras que, de acuerdo con las leyes de Kepler del movimiento planetario (basadas en la conservación del momento angular ) y la conservación de la energía, estas dos cantidades son constantes para una órbita dada:
dónde:
- es la distancia desde el apocentro al foco primario
- es la distancia desde el pericentro hasta el foco primario
- a es el semieje mayor :
- μ es el parámetro gravitacional estándar
- e es la excentricidad , definida como
Téngase en cuenta que para convertir las alturas sobre la superficie en distancias entre una órbita y su principal, debe sumarse el radio del cuerpo central, y viceversa.
La media aritmética de las dos distancias límite es la longitud del semieje mayor a . La media geométrica de las dos distancias es la longitud del semieje menor b .
La media geométrica de las dos velocidades límite es
cual es la velocidad de un cuerpo en una órbita circular cuyo radio es .
Tiempo del perihelio
Los elementos orbitales, como el momento del paso por el perihelio, se definen en la época elegida utilizando una solución de dos cuerpos no perturbada que no tiene en cuenta el problema de n cuerpos . Para obtener un momento preciso del paso por el perihelio, es necesario utilizar una época cercana al paso por el perihelio. Por ejemplo, utilizando una época de 1996, el cometa Hale–Bopp muestra el perihelio el 1 de abril de 1997. [28] Utilizando una época de 2008 se muestra una fecha de perihelio menos precisa del 30 de marzo de 1997. [29] Los cometas de período corto pueden ser incluso más sensibles a la época seleccionada. Utilizando una época de 2005 se muestra que 101P/Chernykh llega al perihelio el 25 de diciembre de 2005, [30] pero utilizando una época de 2012 se produce una fecha de perihelio no perturbada menos precisa del 20 de enero de 2006. [31]
| Época | Fecha del perihelio (tp) |
|---|---|
| 2010 | 19.892 de abril de 2024 |
| n-cuerpo [32] | 21 de abril de 2024.139 |
| 2018 | 23 de abril de 2024.069 |
La integración numérica muestra que el planeta enano Eris llegará al perihelio alrededor de diciembre de 2257. [33] El uso de una época de 2021, que es 236 años antes, muestra con menor precisión que Eris llegará al perihelio en 2260. [34]
4 Vesta llegó al perihelio el 26 de diciembre de 2021, [35] pero el uso de una solución de dos cuerpos en una época de julio de 2021 muestra con menor precisión que Vesta llegó al perihelio el 25 de diciembre de 2021. [36]
Arcos cortos
Los objetos transneptunianos descubiertos a más de 80 UA del Sol necesitan decenas de observaciones a lo largo de varios años para delimitar bien sus órbitas porque se mueven muy lentamente en relación con las estrellas de fondo. Debido a las estadísticas de números pequeños, los objetos transneptunianos como 2015 TH 367 , cuando solo tuvo 8 observaciones a lo largo de un arco de observación de 1 año, que no han llegado o no llegarán al perihelio durante aproximadamente 100 años, pueden tener una incertidumbre de 1 sigma de 77,3 años (28 220 días) en la fecha del perihelio. [37]
Véase también
- Distancia de aproximación más cercana
- Anomalía excéntrica
- Vuelo espacial
- Trayectoria hiperbólica § Aproximación más cercana
- Anomalía media
- Sistema de coordenadas perifocales
- Verdadera anomalía
Referencias
- ^ "ápside". Dictionary.com Unabridged (en línea). nd
- ^ "ápside". Diccionario American Heritage de la lengua inglesa (quinta edición). HarperCollins.
- ^ Joe Rao (6 de julio de 2023). "¡Feliz Día del Afelio! Hoy la Tierra se encuentra en su punto más alejado del Sol en 2023". Space.com . Consultado el 22 de abril de 2024 .
- ^ "Baricentro Tierra-Luna - SkyMarvels.com" www.skymarvels.com . Consultado el 23 de abril de 2024 .
- ^ ab Dado que el Sol, Ἥλιος en griego, comienza con una vocal (H es la vocal ē larga en griego), la o final en "apo" se omite del prefijo. =La pronunciación "Ap-helion" se da en muchos diccionarios [1] Archivado el 22 de diciembre de 2015 en Wayback Machine , pronunciando la "p" y la "h" en sílabas separadas. Sin embargo, la pronunciación / ə ˈ f iː l i ə n / [2] Archivado el 29 de julio de 2017 en Wayback Machine también es común ( por ejemplo, McGraw Hill Dictionary of Scientific and Technical Terms, 5.ª edición, 1994, pág. 114), ya que en griego tardío, 'p' de ἀπό seguida de la 'h' de ἥλιος se convierte en phi; Por lo tanto, la palabra griega es αφήλιον. (ver, por ejemplo, Walker, John, A Key to the Classical Pronunciation of Greek, Latin, and Scripture Proper Names , Townsend Young 1859 [3] Archivado el 21 de septiembre de 2019 en Wayback Machine , página 26). Muchos [4] diccionarios dan ambas pronunciaciones.
- ^ Chisholm, Hugh , ed. (1911). . Encyclopædia Britannica . Vol. 21 (11.ª ed.). Cambridge University Press. pág. 149.
- ^ abcd «Conceptos básicos de los vuelos espaciales». NASA. Archivado desde el original el 30 de septiembre de 2019. Consultado el 30 de mayo de 2017 .
- ^ Klein, Ernest, A Comprehensive Etymological Dictionary of the English Language , Elsevier, Ámsterdam, 1965. (Versión archivada)
- ^ "Informe de la misión Apolo 15". Glosario . Archivado desde el original el 19 de marzo de 2010 . Consultado el 16 de octubre de 2009 .
- ^ R. Dendy; D. Zeleznikar; M. Zemba (27 de septiembre de 2021). Enlaces de comunicaciones de elementos de propulsión y potencia de la NASA Lunar Exploration – Gateway. 38.ª Conferencia Internacional de Sistemas de Comunicaciones por Satélite (ICSSC). Arlington, VA. Archivado desde el original el 29 de marzo de 2022. Consultado el 18 de julio de 2022 .
- ^ Frank, J.; Rees, MJ (1 de septiembre de 1976). "Efectos de agujeros negros masivos en sistemas estelares densos". MNRAS . 176 (6908): 633–646. Bibcode :1976MNRAS.176..633F. doi : 10.1093/mnras/176.3.633 .
- ^ Perimelasma Archivado el 25 de febrero de 2019 en Wayback Machine , por Geoffrey Landis, publicado por primera vez en Asimov's Science Fiction , enero de 1998, republicado en Infinity Plus
- ^ R. Schödel; T. Ott; R. Genzel; R. Hofmann; M. Lehnert; A. Eckart; N. Mouawad; T. Alexander; MJ Reid; R. Lenzen; M. Hartung; F. Lacombe; D. Rouan; E. Gendron; G. Rousset; A.-M. Lagrange; W. Brandner; N. Ageorges; C. Lidman; AFM Moorwood; J. Spyromilio; N. Hubin; KM Menten (17 de octubre de 2002). "Una estrella en una órbita de 15,2 años alrededor del agujero negro supermasivo en el centro de la Vía Láctea". Nature . 419 (6908): 694–696. arXiv : astro-ph/0210426 . Código Bibliográfico :2002Natur.419..694S. : Nature01121. PMID 12384690. S2CID 4302128.
- ^ "MAVEN » Science Orbit". Archivado desde el original el 8 de noviembre de 2018 . Consultado el 7 de noviembre de 2018 .
- ^ "Dawn Journal: 11 años en el espacio". www.planetary.org . Archivado desde el original el 24 de octubre de 2018. Consultado el 24 de octubre de 2018 .
- ^ Cecconi, B.; Lamy, L.; Zarka, P.; Prangé, R.; Kurth, WS; Louarn, P. (4 de marzo de 2009). «Estudio goniopolarimétrico de la pericrona de revolución 29 utilizando el receptor de radio de alta frecuencia del instrumento Cassini Radio and Plasma Wave Science». Journal of Geophysical Research: Space Physics . 114 (A3): A03215. Bibcode :2009JGRA..114.3215C. doi :10.1029/2008JA013830. Archivado desde el original el 9 de diciembre de 2019 . Consultado el 9 de diciembre de 2019 en ui.adsabs.harvard.edu.
- ^ Ejemplo de uso: McKevitt, James; Bulla, Sophie; Dixon, Tom; Criscola, Franco; Parkinson-Swift, Jonathan; Bornberg, Christina; Singh, Jaspreet; Patel, Kuren; Laad, Aryan; Forder, Ethan; Ayin-Walsh, Louis; Beegadhur, Shayne; Wedde, Paul; Pappula, Bharath Simha Reddy; McDougall, Thomas; Foghis, Madalin; Kent, Jack; Morgan, James; Raj, Utkarsh; Heinreichsberger, Carina (18 de junio de 2021). "Un observatorio multifunción y plataforma científica de clase L para Neptuno". Actas de la Conferencia Mundial de Exploración Espacial de 2021 . arXiv : 2106.09409 .
- ^ "la definición de ábside". Dictionary.com . Archivado desde el original el 8 de diciembre de 2015. Consultado el 28 de noviembre de 2015 .
- ^ Darling, David. «Línea de nodos». The Encyclopedia of Astrobiology, Astronomy, and Spaceflight . Archivado desde el original el 23 de agosto de 2019. Consultado el 17 de mayo de 2007 .
- ^ "Perihelio, afelio y solsticios". timeanddate.com. Archivado desde el original el 3 de enero de 2018. Consultado el 10 de enero de 2018 .
- ^ "Variación en los tiempos de perihelio y afelio". Departamento de Aplicaciones Astronómicas del Observatorio Naval de los Estados Unidos. 11 de agosto de 2011. Archivado desde el original el 11 de enero de 2018 . Consultado el 10 de enero de 2018 .
- ^ "Exploración del Sistema Solar: Ciencia y Tecnología: Características científicas: ¿Tiempo, tiempo, en todas partes?". NASA . Archivado desde el original el 29 de septiembre de 2015. Consultado el 19 de septiembre de 2015 .
- ^ "La Tierra en el afelio". Clima espacial. Julio de 2008. Archivado desde el original el 17 de julio de 2015 . Consultado el 7 de julio de 2015 .
- ^ Rockport, Steve C. "¿Cuánto afecta el afelio a nuestro clima? Estamos en el afelio en verano. ¿Serían nuestros veranos más cálidos si estuviéramos en el perihelio?". Planetario . Universidad del Sur de Maine . Archivado desde el original el 6 de julio de 2020 . Consultado el 4 de julio de 2020 .
- ^ "Data.GISS: Parámetros orbitales de la Tierra". data.giss.nasa.gov . Archivado desde el original el 2 de octubre de 2015.
- ^ Espenak, Fred. «La Tierra en el perihelio y el afelio: 2001 a 2100». astropixels . Archivado desde el original el 13 de julio de 2021 . Consultado el 24 de junio de 2021 .
- ^ "Cuadro comparativo planetario de la NASA". Archivado desde el original el 4 de agosto de 2016 . Consultado el 4 de agosto de 2016 .
- ^ "JPL SBDB: Hale-Bopp (época 1996)". Archivado desde el original el 16 de julio de 2020 . Consultado el 16 de julio de 2020 .
- ^ "JPL SBDB: Hale-Bopp". Archivado desde el original el 17 de julio de 2020 . Consultado el 16 de julio de 2020 .
- ^ "101P/Chernykh - A (NK 1293) de Syuichi Nakano". Archivado desde el original el 3 de octubre de 2020 . Consultado el 17 de julio de 2020 .
- ^ JPL SBDB: 101P/Chernykh (época 2012)
- ^ "Lote de Horizons para 12P/Pons-Brooks (90000223) a las 03:20 del 21 de abril de 2024" (El perihelio se produce cuando el rdot cambia de negativo a positivo). JPL Horizons . Archivado desde el original el 12 de febrero de 2023 . Consultado el 11 de febrero de 2023 .(Fecha de resolución del JPL#K242/3: 24 de octubre de 2022)
- ^ "Lote de datos de Horizons para Eris en el perihelio alrededor del 7 de diciembre de 2257 ±2 semanas". JPL Horizons (El perihelio ocurre cuando rdot cambia de negativo a positivo. La base de datos SBDB del JPL enumera de manera genérica (incorrecta) una fecha de perihelio de dos cuerpos no perturbado en 2260). Laboratorio de Propulsión a Chorro. Archivado desde el original el 13 de septiembre de 2021 . Consultado el 13 de septiembre de 2021 .
- ^ "JPL SBDB: Eris (Epoch 2021)". Archivado desde el original el 31 de enero de 2018. Consultado el 5 de enero de 2021 .
- ^ "Lote de Horizons para 4 Vesta el 26 de diciembre de 2021" (El perihelio se produce cuando el rdot cambia de negativo a positivo). JPL Horizons . Archivado desde el original el 26 de septiembre de 2021. Consultado el 26 de septiembre de 2021 .(Época 01-Jul-2021/Fecha sol.: 13-Abr-2021)
- ^ JPL SBDB: 4 Vesta (época 2021)
- ^ "JPL SBDB: 2015 TH367". Archivado desde el original el 14 de marzo de 2018. Consultado el 23 de septiembre de 2021 .
{{cite web}}: CS1 maint: bot: original URL status unknown (link)
Enlaces externos
- Comparación de tamaños fotográficos entre apogeo y perigeo, perseus.gr
- Comparación fotográfica del tamaño del afelio y el perihelio, perseus.gr
- Estaciones de la Tierra: equinoccios, solsticios, perihelio y afelio, 2000-2020 Archivado el 13 de octubre de 2007 en Wayback Machine , usno.navy.mil
- Fechas y horas del perihelio y afelio de la Tierra, 2000-2025 Archivado el 13 de octubre de 2007 en Wayback Machine desde el Observatorio Naval de los Estados Unidos
- Lista de asteroides actualmente más cercanos al Sol que Mercurio (Estos objetos estarán cerca del perihelio)
- Lista SBDB del JPL de asteroides del cinturón principal (H<8) ordenados por fecha de perihelio