Apertura numérica

En óptica , la apertura numérica ( NA ) de un sistema óptico es un número adimensional que caracteriza el rango de ángulos en los que el sistema puede aceptar o emitir luz. Al incorporar el índice de refracción en su definición, NA tiene la propiedad de que es constante para un haz a medida que pasa de un material a otro, siempre que no haya poder refractivo en la interfaz. La definición exacta del término varía ligeramente entre diferentes áreas de la óptica. La apertura numérica se usa comúnmente en microscopía para describir el cono de aceptación de un objetivo (y, por lo tanto, su capacidad de captación de luz y resolución ), y en fibra óptica , en la que describe el rango de ángulos dentro de los cuales la luz que incide sobre la fibra se transmitirá a lo largo de ella.

En la mayoría de las áreas de la óptica, y especialmente en microscopía , la apertura numérica de un sistema óptico como una lente objetivo se define por

$${\displaystyle \mathrm {NA} =n\sin \theta,}$$

donde n es el índice de refracción del medio en el que trabaja la lente (1,00 para aire , 1,33 para agua pura y, típicamente, 1,52 para aceite de inmersión ; ^[1] véase también la lista de índices de refracción ), y θ es el semiángulo del cono máximo de luz que puede entrar o salir de la lente. En general, este es el ángulo del rayo marginal real en el sistema. Debido a que se incluye el índice de refracción, la NA de un haz de rayos es invariante a medida que un haz de rayos pasa de un material a otro a través de una superficie plana. Esto se demuestra fácilmente reordenando la ley de Snell para encontrar que n sen θ es constante a través de una interfaz.

En el aire, la apertura angular de la lente es aproximadamente el doble de este valor (dentro de la aproximación paraxial ). La apertura angular generalmente se mide con respecto a un objeto o punto de imagen en particular y variará a medida que se mueva ese punto. En microscopía, la apertura angular generalmente se refiere a la apertura numérica del espacio del objeto a menos que se indique lo contrario.

En microscopía, la apertura numérica es importante porque indica el poder de resolución de una lente. El tamaño del detalle más fino que se puede resolver (la resolución ) es proporcional a ⁠la/2NA⁠ , donde λ es la longitud de onda de la luz. Una lente con una apertura numérica mayor podrá visualizar detalles más finos que una lente con una apertura numérica menor. Suponiendo una óptica de calidad ( limitada por difracción ), las lentes con aperturas numéricas mayores recolectan más luz y generalmente proporcionarán una imagen más brillante, pero proporcionarán una profundidad de campo menor .

La apertura numérica se utiliza para definir el "tamaño del hoyo" en los formatos de discos ópticos . ^[2]

Aumentando el aumento y la apertura numérica del objetivo se reduce la distancia de trabajo, es decir, la distancia entre la lente frontal y la muestra.

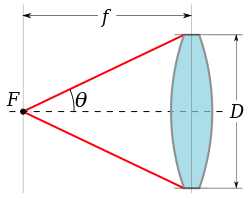
La apertura numérica no se utiliza normalmente en fotografía . En cambio, la apertura angular de una lente (o de un espejo de imagen) se expresa mediante el número f , escritoF / N, donde N es el número f dado por la relación entre la distancia focal f y el diámetro de la pupila de entrada D :

$${\displaystyle N={\frac {f}{D}}.}$$

Esta relación está relacionada con la apertura numérica del espacio de la imagen cuando la lente está enfocada al infinito. ^[3] Según el diagrama de la derecha, la apertura numérica del espacio de la imagen de la lente es:

$${\displaystyle {\text{NA}}_{\text{i}}=n\sin \theta =n\sin \left[\arctan \left({\frac {D}{2f}}\right)\right]\approx n{\frac {D}{2f}},}$$

por lo tanto N ≈ ⁠1/2NA _yo⁠ , asumiendo un uso normal en el aire ( n = 1 ).

La aproximación se mantiene cuando la apertura numérica es pequeña, pero resulta que para sistemas ópticos bien corregidos como lentes de cámara, un análisis más detallado muestra que N es casi exactamente igual a 1/(2NA _i ) incluso en grandes aperturas numéricas. Como explica Rudolf Kingslake, "Es un error común suponer que la relación [ D /2 ​​f ] es en realidad igual a tan θ , y no sen θ ... La tangente, por supuesto, sería correcta si los planos principales fueran realmente planos. Sin embargo, la teoría completa de la condición del seno de Abbe muestra que si una lente se corrige por coma y aberración esférica , como deben ser todos los buenos objetivos fotográficos, el segundo plano principal se convierte en una porción de una esfera de radio f centrada alrededor del punto focal". ^[4] En este sentido, la definición e ilustración tradicional de lentes delgadas del número f es engañosa, y definirlo en términos de apertura numérica puede ser más significativo.

El número f describe la capacidad de captación de luz del objetivo en el caso en que los rayos marginales del lado del objeto sean paralelos al eje del objetivo. Este caso se da con frecuencia en fotografía, donde los objetos que se fotografían suelen estar lejos de la cámara. Sin embargo, cuando el objeto no está alejado del objetivo, la imagen ya no se forma en el plano focal del objetivo y el número f ya no describe con precisión la capacidad de captación de luz del objetivo ni la apertura numérica del lado de la imagen. En este caso, la apertura numérica está relacionada con lo que a veces se denomina " número f de trabajo " o "número f efectivo".

El número f de trabajo se define modificando la relación anterior, teniendo en cuenta la ampliación del objeto a la imagen:

$${\displaystyle {\frac {1}{2{\text{NA}}_{\text{i}}}}=N_{\text{w}}=\left(1-{\frac {m}{P}}\right)N,}$$

donde N _w es el número f de trabajo, m es el aumento de la lente para un objeto a una distancia particular, P es el aumento de la pupila y la NA se define en términos del ángulo del rayo marginal como antes. ^{[3] [5]} El aumento aquí es típicamente negativo, y la mayoría de las veces se supone que el aumento de la pupila es 1 —como explica Allen R. Greenleaf, "La iluminancia varía inversamente al cuadrado de la distancia entre la pupila de salida de la lente y la posición de la placa o película. Debido a que la posición de la pupila de salida generalmente es desconocida para el usuario de una lente, se usa en su lugar la distancia focal conjugada trasera; el error teórico resultante así introducido es insignificante con la mayoría de los tipos de lentes fotográficas". ^[6]

En fotografía, el factor se escribe a veces como 1 + m , donde m representa el valor absoluto del aumento; en cualquier caso, el factor de corrección es 1 o mayor. Las dos igualdades de la ecuación anterior son tomadas por varios autores como la definición del número f de trabajo, como lo ilustran las fuentes citadas. No son necesariamente exactas, pero a menudo se las trata como si lo fueran.

Por el contrario, la apertura numérica del lado del objeto está relacionada con el número f a través del aumento (que tiende a cero para un objeto distante):

$${\displaystyle {\frac {1}{2{\text{NA}}_{\text{o}}}}={\frac {mP}{mP}}N.}$$

En física láser , la apertura numérica se define de forma ligeramente diferente. Los rayos láser se dispersan a medida que se propagan, pero lentamente. Lejos de la parte más estrecha del rayo, la dispersión es aproximadamente lineal con la distancia: el rayo láser forma un cono de luz en el "campo lejano". La relación utilizada para definir la apertura numérica del rayo láser es la misma que la utilizada para un sistema óptico.

$${\displaystyle {\text{NA}}=n\sin \theta,}$$

pero θ se define de manera diferente. Los rayos láser normalmente no tienen bordes afilados como el cono de luz que pasa a través de la abertura de una lente. En cambio, la irradiancia cae gradualmente alejándose del centro del rayo. Es muy común que el rayo tenga un perfil gaussiano . Los físicos láser normalmente optan por hacer que θ sea la divergencia del rayo: el ángulo de campo lejano entre el eje del rayo y la distancia desde el eje en la que la irradiancia cae a e ⁻² veces la irradiancia en el eje. La NA de un rayo láser gaussiano se relaciona entonces con su tamaño de punto mínimo ("cintura del rayo") mediante

$${\displaystyle {\text{NA}}\simeq {\frac {\lambda _ {0}}{\pi w_{0}}},}$$

donde λ ₀ es la longitud de onda de vacío de la luz, y 2 w ₀ es el diámetro del haz en su punto más estrecho, medido entre los puntos de irradiancia e ⁻² ("Ancho total en el máximo e ⁻² de la intensidad"). Esto significa que un haz láser que se enfoca en un punto pequeño se dispersará rápidamente a medida que se aleja del foco, mientras que un haz láser de gran diámetro puede permanecer aproximadamente del mismo tamaño a lo largo de una distancia muy larga. Véase también: Ancho del haz gaussiano .

Una fibra óptica multimodo solo propagará la luz que ingresa a la fibra dentro de un cierto rango de ángulos, conocido como el cono de aceptación de la fibra. El semiángulo de este cono se llama ángulo de aceptación , θ _max . Para la fibra multimodo de índice escalonado en un medio dado, el ángulo de aceptación está determinado solo por los índices de refracción del núcleo, el revestimiento y el medio: donde n es el índice de refracción del medio alrededor de la fibra, n _core es el índice de refracción del núcleo de la fibra y n _clad es el índice de refracción del revestimiento . Si bien el núcleo aceptará luz en ángulos más altos, esos rayos no se reflejarán totalmente en la interfaz núcleo-revestimiento y, por lo tanto, no se transmitirán al otro extremo de la fibra. La derivación de esta fórmula se proporciona a continuación.$${\displaystyle n\sin \theta _{\max }={\sqrt {n_{\text{núcleo}}^{2}-n_{\text{revestimiento}}^{2}}},}$$

Cuando un rayo de luz incide desde un medio de índice de refracción n al núcleo de índice _n en el ángulo de máxima aceptación, la ley de Snell en la interfaz medio-núcleo da$${\displaystyle n\sin \theta _{\max }=n_{\text{núcleo}}\sin \theta _{r}.\ }$$

De la geometría de la figura anterior tenemos:$${\displaystyle \sin \theta _ {r}=\sin \left({90^{\circ }}-\theta _ {c}\right)=\cos \theta _ {c}}$$

dónde$${\displaystyle \theta _{c}=\arcsin {\frac {n_{\text{revestido}}}{n_{\text{núcleo}}}}}$$

es el ángulo crítico para la reflexión interna total .

Sustituyendo cos θ _c por sen θ _r en la ley de Snell obtenemos:$${\displaystyle {\frac {n}{n_{\text{núcleo}}}}\sin \theta _{\max }=\cos \theta _{c}.}$$

Al cuadrar ambos lados$${\displaystyle {\frac {n^{2}}{n_{\text{núcleo}}^{2}}}\sin ^{2}\theta _{\max }=\cos ^{2}\theta _{c}=1-\sin ^{2}\theta _{c}=1-{\frac {n_{\text{revestido}}^{2}}{n_{\text{núcleo}}^{2}}}.}$$

Resolviendo, encontramos la fórmula enunciada anteriormente:

$${\displaystyle n\sin \theta _{\max }={\sqrt {n_{\text{núcleo}}^{2}-n_{\text{revestimiento}}^{2}}},}$$

Esta tiene la misma forma que la apertura numérica en otros sistemas ópticos, por lo que se ha vuelto común definir la NA de cualquier tipo de fibra como$${\displaystyle \mathrm {NA} ={\sqrt {n_{\text{núcleo}}^{2}-n_{\text{revestimiento}}^{2}}},}$$

donde n _núcleo es el índice de refracción a lo largo del eje central de la fibra. Nótese que cuando se utiliza esta definición, la conexión entre la apertura numérica y el ángulo de aceptación de la fibra se convierte solo en una aproximación. En particular, " NA " definido de esta manera no es relevante para la fibra monomodo . ^{[7] [8]} No se puede definir un ángulo de aceptación para la fibra monomodo basándose solo en los índices de refracción.

El número de modos ligados , el volumen del modo , está relacionado con la frecuencia normalizada y, por tanto, con la apertura numérica.

En las fibras multimodo, a veces se utiliza el término apertura numérica de equilibrio , que hace referencia a la apertura numérica con respecto al ángulo de salida extremo de un rayo que emerge de una fibra en la que se ha establecido una distribución modal de equilibrio .

• número f
• Apertura numérica de lanzamiento
• Rayo guiado , contexto de fibra óptica
• Ángulo de aceptación (concentrador solar) , contexto adicional

•  Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022. (en apoyo de MIL-STD-188 ).

• "Objetivos del microscopio: apertura numérica y resolución" por Mortimer Abramowitz y Michael W. Davidson, Molecular Expressions: Optical Microscopy Primer (sitio web), Florida State University , 22 de abril de 2004.
• "Conceptos básicos y fórmulas en microscopía: apertura numérica" ​​por Michael W. Davidson, Nikon MicroscopyU (sitio web).
• "Apertura numérica", Enciclopedia de Física y Tecnología Láser (sitio web).
• "Apertura numérica y resolución", Instalaciones centrales de microscopía del Instituto de investigación cerebral de la UCLA (sitio web), 2007.