Algoritmo de flujo máximo push-reetiquetado

En optimización matemática , el algoritmo push-relabel (alternativamente, algoritmo preflow-push ) es un algoritmo para calcular flujos máximos en una red de flujo . El nombre "push-relabel" proviene de las dos operaciones básicas utilizadas en el algoritmo. A lo largo de su ejecución, el algoritmo mantiene un "preflow" y lo convierte gradualmente en un flujo máximo moviendo el flujo localmente entre nodos vecinos utilizando operaciones push bajo la guía de una red admisible mantenida por operaciones de reetiquetado . En comparación, el algoritmo Ford-Fulkerson realiza aumentos globales que envían el flujo siguiendo caminos desde la fuente hasta el sumidero. ^[1]

El algoritmo push-relabel se considera uno de los algoritmos de flujo máximo más eficientes. El algoritmo genérico tiene una complejidad temporal O ( V  ² E ) fuertemente polinomial , que es asintóticamente más eficiente que el algoritmo O ( VE  ² ) de Edmonds–Karp . ^[2] Las variantes específicas de los algoritmos logran complejidades temporales incluso menores. La variante basada en la regla de selección de nodo de etiqueta más alta tiene una complejidad temporal O ( V  ² √ E ) y generalmente se considera como el punto de referencia para los algoritmos de flujo máximo. ^{[3] [4] La complejidad temporal} O ( VE log( V  ² / E )) subcúbica se puede lograr utilizando árboles dinámicos , aunque en la práctica es menos eficiente. ^[2]

El algoritmo push-relabel se ha ampliado para calcular flujos de costo mínimo . ^[5] La idea de las etiquetas de distancia ha llevado a un algoritmo de ruta de aumento más eficiente, que a su vez se puede incorporar nuevamente al algoritmo push-relabel para crear una variante con un rendimiento empírico aún mayor. ^{[4] [6]}

El concepto de preflujo fue diseñado originalmente por Alexander V. Karzanov y fue publicado en 1974 en Soviet Mathematical Dokladi 15. Este algoritmo de preflujo también utilizó una operación de empuje; sin embargo, utilizó distancias en la red auxiliar para determinar dónde empujar el flujo en lugar de un sistema de etiquetado. ^{[2] [7]}

El algoritmo push-relabel fue diseñado por Andrew V. Goldberg y Robert Tarjan . El algoritmo fue presentado inicialmente en noviembre de 1986 en STOC '86: Proceedings of the eightth annual ACM symposium on Theory of computing, y luego oficialmente en octubre de 1988 como un artículo en el Journal of the ACM. Ambos artículos detallan una forma genérica del algoritmo que termina en O ( V  ² E ) junto con una implementación secuencial O ( V  ³ ) , una implementación O ( VE  log( V  ² / E )) utilizando árboles dinámicos y una implementación paralela/distribuida. ^{[2] [8]} Como se explica en, ^[9] Goldberg-Tarjan introdujo las etiquetas de distancia incorporándolas al algoritmo de flujo máximo paralelo de Yossi Shiloach y Uzi Vishkin . ^[10]

Dejar:

• G = ( V , E ) sea una red con función de capacidad c : V × V → _∞${\displaystyle \mathbb {R}}$ ,
• F = ( G , c , s , t ) una red de flujo , donde s ∈ V y t ∈ V son los vértices fuente y sumidero elegidosrespectivamente,
• f  : V × V →${\displaystyle \mathbb {R}}$ denota un preflujo en F ,
• x _f  : V →${\displaystyle \mathbb {R}}$ denota la función de exceso con respecto al flujo f , definida por x _f ( u ) = Σ _{v ∈ V} f ( v , u ) − Σ _{v ∈ V} f ( u , v ) ,
• c _f  : V × V → _∞${\displaystyle \mathbb {R}}$ denota la función de capacidad residual con respecto al flujo f , definida por c _f  ( e ) = c ( e ) − f  ( e ) ,
• E _f ⊂ E siendo las aristas donde f < c ,

y

• G _f ( V , E _f  ) denota la red residual de G con respecto al flujo f .

El algoritmo push-relabel utiliza una función de etiquetado válida de número entero no negativo que hace uso de etiquetas de distancia o alturas en los nodos para determinar qué arcos se deben seleccionar para la operación push. Esta función de etiquetado se denota por 𝓁 : V →${\displaystyle \mathbb {N}}$ . Esta función debe satisfacer las siguientes condiciones para ser considerada válida:

Etiquetado válido :

𝓁( u ) ≤ 𝓁( v ) + 1 para todo ( u , v ) ∈ E _f

Condición de la fuente :

𝓁( s ) = |  V  |

Conservación del fregadero :

𝓁( t ) = 0

En el algoritmo, los valores de etiqueta de s y t son fijos. 𝓁( u ) es un límite inferior de la distancia no ponderada de u a t en G _f   si t es alcanzable desde u . Si u ha sido desconectado de t , entonces 𝓁( u ) − |  V  | es un límite inferior de la distancia no ponderada de u a s . Como resultado, si existe una función de etiquetado válida, no hay caminos s - t en G _f   porque ningún camino de ese tipo puede ser más largo que |  V  | − 1 .

Un arco ( u , v ) ∈ E _f   se llama admisible si 𝓁( u ) = 𝓁( v ) + 1 . La red admisible G̃ _f ( V , Ẽ _f  ) está compuesta por el conjunto de arcos e ∈ E _f   que son admisibles. La red admisible es acíclica.

Para un flujo fijo f , un vértice v ∉ { s, t } se llama activo si tiene exceso positivo con respecto a f , es decir, x _f ( u ) > 0 .

El algoritmo comienza creando un gráfico residual, inicializando los valores de preflujo a cero y realizando un conjunto de operaciones de inserción de saturación en los arcos residuales ( s , v ) que salen de la fuente, donde v ∈ V \ { s } . De manera similar, las etiquetas se inicializan de modo que la etiqueta en la fuente sea el número de nodos en el gráfico, 𝓁( s ) = |  V  | , y a todos los demás nodos se les asigna una etiqueta de cero. Una vez que se completa la inicialización, el algoritmo realiza repetidamente las operaciones de inserción o reetiquetado contra los nodos activos hasta que no se pueda realizar ninguna operación aplicable.

La operación de empuje se aplica sobre un arco de salida admisible ( u , v ) de un nodo activo u en G _f . Mueve min{ x _f ( u ), c _​​f ( u , v )} unidades de flujo desde u hasta v .

empujar(u, v): afirmar x f [u] > 0 y 𝓁[u] == 𝓁[v] + 1 Δ = mín(x f [u], c[u][v] - f[u][v]) f[u][v] += Δ f[v][u] -= Δ x f [u] -= Δ x f [v] += Δ

Una operación de empuje que hace que f  ( u , v ) alcance c ( u , v ) se denomina empuje saturante , ya que utiliza toda la capacidad disponible del arco residual. De lo contrario, todo el exceso en el nodo se empuja a través del arco residual. Esto se denomina empuje no saturado o no saturado .

La operación de reetiquetado se aplica a un nodo activo u que no es ni la fuente ni el sumidero sin ningún arco de salida admisible en G _f . Modifica 𝓁( u ) para que sea el valor mínimo de modo que se cree un arco de salida admisible. Nótese que esto siempre aumenta 𝓁( u ) y nunca crea un arco empinado, que es un arco ( u , v ) tal que c _f  ( u , v ) > 0 , y 𝓁( u ) > 𝓁( v ) + 1 .

reetiquetar(u): afirmar x f [u] > 0 y 𝓁[u] <= 𝓁[v] para todo v tal que c f [u][v] > 0 𝓁[u] = 1 + min(𝓁[v] para todo v tal que c f [u][v] > 0)

Después de una operación de inserción o reetiquetado, 𝓁 sigue siendo una función de etiquetado válida con respecto a f .

Para una operación de empuje sobre un arco admisible ( u , v ) , puede agregar un arco ( v , u ) a E _f , donde 𝓁( v ) = 𝓁( u ) − 1 ≤ 𝓁( u ) + 1 ; también puede eliminar el arco ( u , v ) de E _f , donde efectivamente elimina la restricción 𝓁( u ) ≤ 𝓁( v ) + 1 .

Para ver que una operación de reetiquetado en el nodo u preserva la validez de 𝓁( u ) , observe que esto está trivialmente garantizado por definición para los arcos exteriores de u en G _f . Para los arcos interiores de u en G _f , el 𝓁( u ) aumentado solo puede satisfacer las restricciones de manera menos estricta, no violarlas.

El algoritmo genérico de inserción y reetiquetado se utiliza solo como prueba de concepto y no contiene detalles de implementación sobre cómo seleccionar un nodo activo para las operaciones de inserción y reetiquetado. Esta versión genérica del algoritmo terminará en O ( V ² E ) .

Dado que 𝓁( s ) = |  V  | , 𝓁( t ) = 0 , y no hay caminos más largos que |  V  | − 1 en G _f , para que 𝓁( s ) satisfaga la condición de etiquetado válido , s debe estar desconectado de t . En la inicialización, el algoritmo cumple este requisito creando un preflujo f que satura todos los arcos de salida de s , después de lo cual 𝓁( v ) = 0 es trivialmente válido para todos los v ∈ V \ { s , t } . Después de la inicialización, el algoritmo ejecuta repetidamente una operación de inserción o reetiquetado aplicable hasta que no se apliquen tales operaciones, momento en el que el preflujo se ha convertido en un flujo máximo.

genérico-push-relabel(G, c, s, t): Crea un flujo previo f que sature todos los arcos de salida de s sea ​​𝓁[s] = |V| sea 𝓁[v] = 0 para todo v ∈ V \ {s} mientras haya una operación de inserción o reetiquetado aplicable ejecutar la operación

El algoritmo mantiene la condición de que 𝓁 es un etiquetado válido durante su ejecución. Esto se puede probar como cierto examinando los efectos de las operaciones de inserción y reetiquetado en la función de etiqueta 𝓁 . La operación de reetiquetado aumenta el valor de la etiqueta por el mínimo asociado más uno, lo que siempre satisfará la restricción 𝓁( u ) ≤ 𝓁( v ) + 1 . La operación de inserción puede enviar flujo de u a v si 𝓁( u ) = 𝓁( v ) + 1 . Esto puede agregar ( v , u ) a G _f  y puede eliminar ( u , v ) de G _f  . La adición de ( v , u ) a G _f  no afectará el etiquetado válido ya que 𝓁( v ) = 𝓁( u ) − 1 . La eliminación de ( u , v ) de G _f  elimina la restricción correspondiente ya que la propiedad de etiquetado válida 𝓁( u ) ≤ 𝓁( v ) + 1 solo se aplica a arcos residuales en G _f  . ^[8]

Si existe un preflujo f y un etiquetado válido 𝓁 para f , entonces no hay un camino de aumento de s a t en el grafo residual G _f  . Esto se puede demostrar por contradicción basada en desigualdades que surgen en la función de etiquetado al suponer que existe un camino de aumento. Si el algoritmo termina, entonces todos los nodos en V \ { s , t } no están activos. Esto significa que todos los v ∈ V \ { s , t } no tienen exceso de flujo, y sin exceso el preflujo f obedece la restricción de conservación de flujo y puede considerarse un flujo normal. Este flujo es el flujo máximo según el teorema de corte mínimo de flujo máximo ya que no hay un camino de aumento de s a t . ^[8]

Por lo tanto, el algoritmo devolverá el flujo máximo al finalizar.

Para limitar la complejidad temporal del algoritmo, debemos analizar la cantidad de operaciones de inserción y reetiquetado que ocurren dentro del bucle principal. La cantidad de operaciones de reetiquetado, inserción con saturación y no saturación se analizan por separado.

En el algoritmo, la operación de reetiquetado se puede realizar como máximo (2|  V  | − 1)(|  V  | − 2) < 2|  V  | ² veces. Esto se debe a que el valor de etiquetado 𝓁( u ) para cualquier nodo u nunca puede disminuir, y el valor máximo de la etiqueta es como máximo 2|  V  | − 1 para todos los nodos. Esto significa que la operación de reetiquetado podría realizarse potencialmente 2|  V  | − 1 veces para todos los nodos V \ { s , t } (es decir, |  V  | − 2 ). Esto da como resultado un límite de O ( V  ² ) para la operación de reetiquetado.

Cada empuje de saturación en un arco admisible ( u , v ) elimina el arco de G _f  . Para que el arco se vuelva a insertar en G _f  para otro empuje de saturación, v primero debe reetiquetarse, seguido de un empuje en el arco ( v , u ) , luego u debe reetiquetarse. En el proceso, 𝓁( u ) aumenta al menos en dos. Por lo tanto, hay O ( V ) empujes de saturación en ( u , v ) , y el número total de empujes de saturación es como máximo 2|  V  ||  E  | . Esto da como resultado un límite de tiempo de O ( VE ) para las operaciones de empuje de saturación.

La limitación del número de empujes no saturantes se puede lograr mediante un argumento potencial . Usamos la función potencial Φ = Σ _{[ u ∈ V ∧ x f  ( u ) > 0]} 𝓁( u ) (es decir, Φ es la suma de las etiquetas de todos los nodos activos). Es obvio que Φ es 0 inicialmente y permanece no negativo durante la ejecución del algoritmo. Tanto los reetiquetados como los empujes saturantes pueden aumentar Φ . Sin embargo, el valor de Φ debe ser igual a 0 al final, ya que no puede haber nodos activos restantes al final de la ejecución del algoritmo. Esto significa que durante la ejecución del algoritmo, los empujes no saturantes deben compensar la diferencia de las operaciones de reetiquetado y empuje saturante para que Φ termine con un valor de 0. La operación de reetiquetado puede aumentar Φ en como máximo (2|  V  | − 1)(|  V  | − 2) . Un empuje saturante sobre ( u , v ) activa v si estaba inactivo antes del empuje, aumentando Φ en como máximo 2|  V  | − 1 . Por lo tanto, la contribución total de todas las operaciones de empuje saturantes a Φ es como máximo (2|  V  | − 1)(2|  V  ||  E  |) . Un empuje no saturante sobre ( u , v ) siempre desactiva u , pero también puede activar v como en un empuje saturante. Como resultado, disminuye Φ en al menos 𝓁( u ) − 𝓁( v ) = 1 . Dado que los reetiquetados y los empujes de saturación aumentan Φ , la cantidad total de empujes no saturantes debe compensar la diferencia de (2|  V  | − 1)(|  V  | − 2) + (2|  V  | − 1)(2|  V  ||  E  |) ≤ 4|  V  | ² |  E  | . Esto da como resultado un límite de tiempo de O ( V  ² E ) para las operaciones de empuje no saturantes.

En resumen, el algoritmo ejecuta O ( V  ² ) reetiquetados, O ( VE ) inserciones saturadas y O ( V  ² E ) inserciones no saturantes. Las estructuras de datos se pueden diseñar para seleccionar y ejecutar una operación aplicable en tiempo O (1) . Por lo tanto, la complejidad temporal del algoritmo es O ( V  ² E ) . ^{[1] [8]}

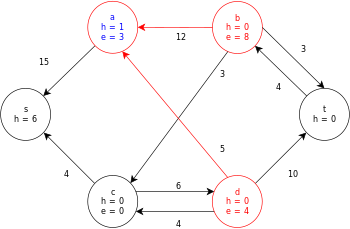
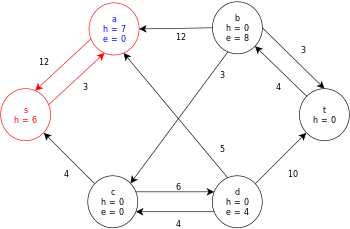
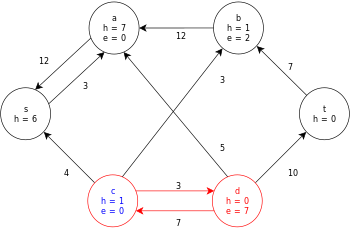
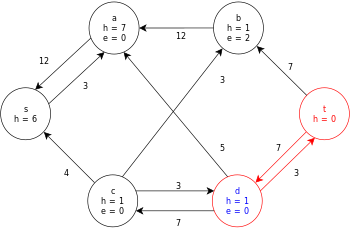
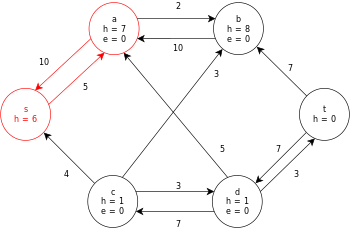
A continuación se muestra una ejecución de muestra del algoritmo genérico push-relabel, como se definió anteriormente, en el siguiente diagrama de gráfico de flujo de red simple.

En el ejemplo, los valores h y e denotan la etiqueta 𝓁 y el exceso x _f  , respectivamente, del nodo durante la ejecución del algoritmo. Cada gráfico residual en el ejemplo solo contiene los arcos residuales con una capacidad mayor que cero. Cada gráfico residual puede contener múltiples iteraciones del bucle de operación de ejecución .

Operación(es) del algoritmo	Gráfica de residuos
Inicialice el gráfico residual estableciendo el preflujo en valores 0 e inicializando el etiquetado.
El empuje de saturación inicial se realiza a través de todos los arcos de preflujo fuera de la fuente, s .
El nodo a se reetiqueta para empujar su exceso de flujo hacia el sumidero, t . El exceso en a se empuja luego hacia b y luego hacia d en dos empujes de saturación subsiguientes; lo que todavía deja a con algo de exceso.
Una vez más, a se vuelve a etiquetar para empujar su exceso a lo largo de su último residuo positivo restante (es decir, empujar el exceso nuevamente a s ). Luego, el nodo a se elimina del conjunto de nodos activos.
Reetiqueta b y luego empuja su exceso hacia t y c .
Vuelva a etiquetar c y luego empuje su exceso hacia d .
Reetiqueta d y luego empuja su exceso hacia t .
Esto deja al nodo b como el único nodo activo restante, pero no puede empujar su exceso de flujo hacia el sumidero. Reetiqueta b y luego empuja su exceso hacia la fuente, s , a través del nodo a .
Empuja el último bit de exceso hacia la fuente, s . No quedan nodos activos. El algoritmo finaliza y devuelve el flujo máximo del gráfico (como se ve arriba).

El ejemplo (pero con flujo inicial de 0) se puede ejecutar aquí de forma interactiva.

Si bien el algoritmo genérico de inserción y reetiquetado tiene una complejidad temporal de O ( V  ² E ) , las implementaciones eficientes logran una complejidad temporal de O ( V  ³ ) o menor al aplicar reglas apropiadas para seleccionar las operaciones de inserción y reetiquetado aplicables. El rendimiento empírico se puede mejorar aún más mediante heurística.

La estructura de datos de "arco actual" es un mecanismo para visitar los vecinos de entrada y salida de un nodo en la red de flujo en un orden circular estático. Si se crea una lista de vecinos enlazada individualmente para un nodo, la estructura de datos puede ser tan simple como un puntero a la lista que recorre la lista y retrocede hasta el principio cuando se sale del final.

En función de la estructura de datos "arco de corriente", se puede definir la operación de descarga. Una operación de descarga se aplica a un nodo activo y empuja repetidamente el flujo desde el nodo hasta que se vuelve inactivo, volviéndolo a etiquetar según sea necesario para crear arcos admisibles en el proceso.

descarga(u): mientras x f [u] > 0 hacer  si el arco actual[u] se ha ido al final de vecinos[u] entonces reetiquetar(u) rebobinar arco actual[u] de lo contrario,  sea (u, v) = arco-corriente[u] si (u, v) es admisible entonces empujar(u, v) deje que current-arc[u] apunte al próximo vecino de u

Encontrar el próximo borde admisible para empujar ha amortizado la complejidad . El puntero del arco actual solo se mueve al próximo vecino cuando el borde del vecino actual está saturado o no es admisible, y ninguna de estas dos propiedades puede cambiar hasta que se vuelva a etiquetar el nodo activo. Por lo tanto, cuando el puntero se va, no hay bordes no saturados admisibles y tenemos que volver a etiquetar el nodo activo , por lo que haber movido el puntero varias veces se paga con la operación de reetiquetado. ^[8]${\estilo de visualización O(1)}$ ${\estilo de visualización u}$${\estilo de visualización u}$${\displaystyle O(V)}$${\displaystyle O(V)}$

La definición de la operación de descarga reduce el algoritmo push-relabel a seleccionar repetidamente un nodo activo para descargar. Según la regla de selección, el algoritmo exhibe diferentes complejidades temporales. Por razones de brevedad, ignoramos s y t cuando hacemos referencia a los nodos en la siguiente discusión.

El algoritmo FIFO push-relabel ^[2] organiza los nodos activos en una cola. Los nodos activos iniciales se pueden insertar en cualquier orden. El algoritmo siempre elimina el nodo que está al frente de la cola para su descarga. Cuando un nodo inactivo se activa, se agrega al final de la cola.

El algoritmo tiene una complejidad temporal de O ( V  ³ ) .

El algoritmo push-relabel de reetiquetado al frente ^[1] organiza todos los nodos en una lista enlazada y mantiene invariable que la lista está ordenada topológicamente con respecto a la red admisible. El algoritmo escanea la lista de adelante hacia atrás y realiza una operación de descarga en el nodo actual si está activo. Si el nodo es reetiquetado, se mueve al frente de la lista y el escaneo se reinicia desde el frente.

El algoritmo también tiene una complejidad temporal O ( V  ³ ) .

El algoritmo push-reetiquetado de etiqueta más alta ^[11] organiza todos los nodos en contenedores indexados por sus etiquetas. El algoritmo siempre selecciona un nodo activo con la etiqueta más grande para descargar.

El algoritmo tiene una complejidad temporal de O ( V  ² √ E ) . Si se utiliza la regla de selección de etiqueta más baja, la complejidad temporal se convierte en O ( V  ² E ) . ^[3]

Aunque en la descripción del algoritmo genérico push-relabel anterior, 𝓁( u ) se establece en cero para cada nodo u excepto s y t al comienzo, es preferible realizar una búsqueda en amplitud hacia atrás desde t para calcular etiquetas exactas. ^[2]

El algoritmo se divide típicamente en dos fases. La fase uno calcula un preflujo máximo descargando solo los nodos activos cuyas etiquetas están por debajo de n . La fase dos convierte el preflujo máximo en un flujo máximo devolviendo el exceso de flujo que no puede alcanzar t a s . Se puede demostrar que la fase dos tiene una complejidad temporal de O ( VE ) independientemente del orden de las operaciones de inserción y reetiquetado y, por lo tanto, está dominada por la fase uno. Alternativamente, se puede implementar utilizando la descomposición del flujo. ^[9]

Las heurísticas son cruciales para mejorar el rendimiento empírico del algoritmo. ^[12] Dos heurísticas comúnmente utilizadas son la heurística de brecha y la heurística de reetiquetado global. ^{[2] [13]} La heurística de brecha detecta brechas en la función de etiquetado. Si hay una etiqueta 0 < 𝓁 ' < |  V  | para la cual no hay ningún nodo u tal que 𝓁( u ) = 𝓁 ' , entonces cualquier nodo u con 𝓁 ' < 𝓁( u ) < |  V  | ha sido desconectado de t y puede ser reetiquetado a (|  V  | + 1) inmediatamente. La heurística de reetiquetado global realiza periódicamente una búsqueda en amplitud hacia atrás desde t en G _f  para calcular las etiquetas exactas de los nodos. Ambas heurísticas omiten operaciones de reetiquetado inútiles, que son un cuello de botella del algoritmo y contribuyen a la ineficacia de los árboles dinámicos. ^[4]

#incluir <stdlib.h> #incluir <stdio.h>  #define NODOS 6 #define MIN(X,Y) ((X) < (Y) ? (X) : (Y)) #define INFINITO 10000000void push ( const int * const * C , int ** F , int * exceso , int u , int v ) { int enviar = MIN ( exceso [ u ], C [ u ][ v ] - F [ u ][ v ]); F [ u ][ v ] += enviar ; F [ v ][ u ] -= enviar ; exceso [ u ] -= enviar ; exceso [ v ] += enviar ; }                                   void relabeat ( const int * const * C , const int * const * F , int * altura , int u ) { int v ; int min_height = INFINITO ; para ( v = 0 ; v < NODOS ; v ++ ) { si ( C [ u ][ v ] - F [ u ][ v ] > 0 ) { min_height = MIN ( min_height , altura [ v ]); altura [ u ] = min_height + 1 ; } } };                                                  descarga nula ( const int * const * C , int ** F , int * exceso , int * altura , int * visto , int u ) { while ( exceso [ u ] > 0 ) { if ( visto [ u ] < NODOS ) { int v = visto [ u ]; if (( C [ u ][ v ] - F [ u ][ v ] > 0 ) && ( altura [ u ] > altura [ v ])) { push ( C , F , exceso , u , v ); } else { visto [ u ] += 1 ; } } else { reetiquetar ( C , F , altura , u ); visto [ u ] = 0 ; } } }                                                                   void moveToFront ( int i , int * A ) { int temp = A [ i ]; int n ; para ( n = i ; n > 0 ; n -- ) { A [ n ] = A [ n -1 ]; } A [ 0 ] = temp ; }                           int pushRelabel ( const int * const * C , int ** F , int fuente , int sumidero ) { int * exceso , * altura , * lista , * visto , i , p ;                      exceso = ( int * ) calloc ( NODOS , tamañode ( int )); altura = ( int * ) calloc ( NODOS , tamañode ( int )); visto = ( int * ) calloc ( NODOS , tamañode ( int ));                  lista = ( int * ) calloc (( NODOS -2 ), tamaño de ( int ));      para ( i = 0 , p = 0 ; i < NODOS ; i ++ ){ si (( i != fuente ) && ( i != sumidero )) { lista [ p ] = i ; p ++ ; } }                          altura [ fuente ] = NODOS ; exceso [ fuente ] = INFINITO ; para ( i = 0 ; i < NODOS ; i ++ ) empujar ( C , F , exceso , fuente , i );                   p = 0 ; mientras ( p < NODOS - 2 ) { int u = lista [ p ]; int altura_anterior = altura [ u ]; descarga ( C , F , exceso , altura , visto , u ); si ( altura [ u ] > altura_anterior ) { moverAlFrente ( p , lista ); p = 0 ; } de lo contrario { p += 1 ; } } int caudal_máximo = 0 ; para ( i = 0 ; i < NODOS ; i ++ ) caudal_máximo += F [ fuente ][ i ];                                                         libre ( lista ); libre ( visto ); libre ( altura ); libre ( exceso );   devolver flujo máximo ; } void printMatriz ( const int * const * M ) { int i , j ; para ( i = 0 ; i < NODOS ; i ++ ) { para ( j = 0 ; j < NODOS ; j ++ ) printf ( "%d \t " , M [ i ][ j ]); printf ( " \n " ); } }                              int main ( void ) { int ** flujo , ** capacidades , i ; flujo = ( int ** ) calloc ( NODOS , tamañode ( int * )); capacidades = ( int ** ) calloc ( NODOS , tamañode ( int * )); para ( i = 0 ; i < NODOS ; i ++ ) { flujo [ i ] = ( int * ) calloc ( NODOS , tamañode ( int )); capacidades [ i ] = ( int * ) calloc ( NODOS , tamañode ( int )); }                                         //Gráfico de muestra capacidades [ 0 ][ 1 ] = 2 ; capacidades [ 0 ][ 2 ] = 9 ; capacidades [ 1 ][ 2 ] = 1 ; capacidades [ 1 ][ 3 ] = 0 ; capacidades [ 1 ][ 4 ] = 0 ; capacidades [ 2 ][ 4 ] = 7 ; capacidades [ 3 ][ 5 ] = 7 ; capacidades [ 4 ][ 5 ] = 4 ;                         printf ( "Capacidad: \n " ); printMatriz ( capacidades );  printf ( "Flujo máximo: \n %d \n " , pushRelabel ( capacidades , flujo , 0 , 5 ));     printf ( "Flujos: \n " ); printMatrix ( flujo );  devuelve 0 ; } 

def  relabel_to_front ( C ,  source :  int ,  sink :  int )  ->  int :  n  =  len ( C )  # C es la matriz de capacidad  F  =  [[ 0 ]  *  n  para  _  en  rango ( n )]  # la capacidad residual de u a v es C[u][v] - F[u][v] altura  =  [ 0 ]  *  n  # altura del nodo  exceso  =  [ 0 ]  *  n  # flujo hacia el nodo menos flujo desde el nodo  visto  =  [ 0 ]  *  n  # vecinos vistos desde la última reetiqueta  # nodo "cola"  lista de nodos  =  [ i  para  i  en  rango ( n )  si  i  !=  origen  y  i  !=  sumidero ] def  push ( u ,  v ):  enviar  =  min ( exceso [ u ],  C [ u ][ v ]  -  F [ u ][ v ])  F [ u ][ v ]  +=  enviar  F [ v ][ u ]  -=  enviar  exceso [ u ]  -=  enviar  exceso [ v ]  +=  enviar def  relabel ( u ):  # Encuentra la nueva altura más pequeña que hace posible un empuje,  # si tal empuje es posible.  min_height  =  ∞  para  v  en  rango ( n ):  si  C [ u ][ v ]  -  F [ u ][ v ]  >  0 :  min_height  =  min ( min_height ,  height [ v ])  height [ u ]  =  min_height  +  1 def  descarga ( u ):  mientras  exceso [ u ]  >  0 :  si  visto [ u ]  <  n :  # comprobar el próximo vecino  v  =  visto [ u ]  si  C [ u ][ v ]  -  F [ u ][ v ]  >  0  y  altura [ u ]  >  altura [ v ]:  empujar ( u ,  v )  de lo contrario :  visto [ u ]  +=  1  de lo contrario :  # hemos comprobado todos los vecinos. debe volver a etiquetar  relabel ( u )  visto [ u ]  =  0 altura [ fuente ]  =  n  # la ruta más larga desde la fuente hasta el sumidero es menor que n largo  exceso [ fuente ]  =  ∞  # enviar tanto flujo como sea posible a los vecinos de la fuente  para  v  en  rango ( n ):  push ( fuente ,  v ) p  =  0  mientras  p  <  len ( lista_de_nodos ):  u  =  lista_de_nodos [ p ]  altura_anterior  =  altura [ u ]  descarga ( u )  si  altura [ u ]  >  altura_anterior :  lista_de_nodos . insert ( 0 ,  lista_de_nodos . pop ( p ))  # moverse al principio de la lista  p  =  0  # comenzar desde el principio de la lista  de lo contrario :  p  +=  1 devuelve  suma ( F [ fuente ])