Método de Duckworth-Lewis-Stern


El método Duckworth–Lewis–Stern ( DLS ) es una formulación matemática diseñada para calcular la puntuación objetivo (número de carreras necesarias para ganar) para el equipo que batea segundo en un partido de cricket de overs limitados interrumpido por el clima u otras circunstancias. El método fue ideado por dos estadísticos ingleses , Frank Duckworth y Tony Lewis , y anteriormente se conocía como el método Duckworth–Lewis ( D/L ). [1] Se introdujo en 1997 y fue adoptado oficialmente por el Consejo Internacional de Críquet (ICC) en 1999. Después del retiro de Duckworth y Lewis, el estadístico australiano Steven Stern se convirtió en el custodio del método, que fue renombrado a su título actual en noviembre de 2014. [2] [3] En 2014, refinó el modelo para que se ajustara mejor a las tendencias de puntuación modernas, especialmente en el cricket T20, lo que resultó en el método Duckworth-Lewis-Stern actualizado. [4] Este método refinado sigue siendo el estándar para manejar partidos afectados por la lluvia en el cricket internacional en la actualidad.
El objetivo de puntuación en los partidos de cricket sin interrupciones es uno más que el número de carreras anotadas por el equipo que bateó primero. Cuando se pierden overs , establecer un objetivo ajustado para el equipo que batea segundo no es tan simple como reducir el objetivo de carreras proporcionalmente a la pérdida de overs, porque un equipo con diez wickets en mano y 25 overs para batear puede jugar de manera más agresiva que si tuviera diez wickets y 50 overs completos, por ejemplo, y, en consecuencia, puede lograr una tasa de carreras más alta . El método DLS es un intento de establecer un objetivo estadísticamente justo para las entradas del segundo equipo, que es la misma dificultad que el objetivo original. El principio básico es que cada equipo en un partido de overs limitados tiene dos recursos disponibles con los que anotar carreras (overs para jugar y wickets restantes), y el objetivo se ajusta proporcionalmente al cambio en la combinación de estos dos recursos.
Historia y creación
Anteriormente se habían utilizado varios métodos diferentes para resolver partidos de cricket afectados por la lluvia, siendo el más común el método de tasa de carrera promedio y, más tarde, el método de overs más productivos .
Si bien estos métodos eran simples por naturaleza, tenían fallas intrínsecas y eran fácilmente explotables:
- El método de la tasa de carreras promedio no tenía en cuenta los wickets perdidos por el equipo que bateaba en segundo lugar, sino que simplemente reflejaba su tasa de puntuación cuando se interrumpía el partido. Si el equipo consideraba que era probable que se produjera una interrupción por lluvia, podía intentar forzar la tasa de puntuación sin tener en cuenta la pérdida de wickets, que era muy probable, lo que significa que cualquier comparación con el equipo que bateaba en primer lugar sería errónea.
- El método de Overs Más Productivos no solo no tuvo en cuenta los wickets perdidos por el equipo que bateó segundo, sino que también penalizó efectivamente al equipo que bateó segundo por un buen bowling al ignorar sus mejores overs al establecer el objetivo revisado.
- Ambos métodos también producían objetivos revisados que frecuentemente alteraban el equilibrio del partido y no tenían en cuenta la situación del partido en el momento de la interrupción.
El método D/L fue ideado por dos estadísticos británicos , Frank Duckworth y Tony Lewis , como resultado del resultado de la semifinal de la Copa del Mundo de 1992 entre Inglaterra y Sudáfrica , donde se utilizó el método de Overs Más Productivos. Cuando la lluvia detuvo el juego durante 12 minutos, Sudáfrica necesitaba 22 carreras de 13 bolas, pero cuando el juego se reanudó, el objetivo revisado dejó a Sudáfrica necesitando 21 carreras de una bola, una reducción de solo una carrera en comparación con una reducción de dos overs, y un objetivo virtualmente imposible dado que la puntuación máxima de una bola es generalmente de seis carreras. [5] Duckworth dijo: "Recuerdo haber escuchado a Christopher Martin-Jenkins en la radio diciendo 'seguramente alguien, en algún lugar, podría llegar a algo mejor' y pronto me di cuenta de que era un problema matemático que requería una solución matemática". [6] [7] El método D/L evita este defecto: en este partido, el objetivo D/L revisado de 236 habría dejado a Sudáfrica necesitando cuatro para empatar o cinco para ganar desde la última bola. [8] [nota 1]
El método D/L se utilizó por primera vez en el cricket internacional el 1 de enero de 1997 en el segundo partido de la serie ODI de Zimbabue contra Inglaterra , que Zimbabue ganó por siete carreras. [11] El método D/L fue adoptado formalmente por la ICC en 1999 como el método estándar para calcular las puntuaciones objetivo en partidos de un día acortados por la lluvia .
Teoría
Resumen del cálculo
La esencia del método D/L son los "recursos". Cada equipo tiene dos "recursos" que puede utilizar para anotar tantas carreras como sea posible: la cantidad de overs que debe recibir y la cantidad de wickets que tiene en la mano. En cualquier momento de cualquier entrada , la capacidad de un equipo para anotar más carreras depende de la combinación de estos dos recursos que le quedan. Si observamos los puntajes históricos, existe una correspondencia muy estrecha entre la disponibilidad de estos recursos y el puntaje final de un equipo, una correspondencia que D/L explota. [12]

El método D/L convierte todas las combinaciones posibles de overs (o, más precisamente, bolas) y wickets restantes en una cifra porcentual combinada de recursos restantes (con 50 overs y 10 wickets = 100 %), y todos estos se almacenan en una tabla publicada o en una computadora. El puntaje objetivo para el equipo que batea en segundo lugar ("Equipo 2") se puede ajustar hacia arriba o hacia abajo a partir del total que logró el equipo que batea primero ("Equipo 1") utilizando estos porcentajes de recursos, para reflejar la pérdida de recursos de uno o ambos equipos cuando un partido se acorta una o más veces.
En la versión de D/L que se usa con más frecuencia en partidos internacionales y de primera clase (la 'Edición Profesional'), el objetivo para el Equipo 2 se ajusta simplemente en proporción a los recursos de los dos equipos, es decir,
Si, como suele ocurrir, este "puntaje par" es un número de carreras no entero , entonces el objetivo del Equipo 2 para ganar es este número redondeado al entero superior, y el puntaje para empatar (también llamado puntaje par), es este número redondeado al entero anterior. Si el Equipo 2 alcanza o supera el puntaje objetivo, entonces habrá ganado el partido. Si el partido termina cuando el Equipo 2 ha alcanzado exactamente (pero no superado) el puntaje par, entonces el partido es un empate. Si el Equipo 2 no logra alcanzar el puntaje par, entonces habrá perdido.
Por ejemplo, si un retraso por lluvia significa que el Equipo 2 solo tiene el 90% de los recursos disponibles, y el Equipo 1 obtuvo 254 puntos con el 100% de los recursos disponibles, entonces 254 × 90% / 100% = 228,6, por lo que el objetivo del Equipo 2 es 229, y el puntaje para empatar es 228. Los valores de recursos reales utilizados en la Edición Profesional no están disponibles públicamente, [13] por lo que se debe utilizar una computadora que tenga este software cargado.
Si se trata de un partido de 50 overs y el Equipo 1 completó sus entradas sin interrupciones, entonces tuvo el 100 % de los recursos disponibles, por lo que la fórmula se simplifica a:
Resumen del impacto en el objetivo del Equipo 2
- Si hay un retraso antes de que comience la primera entrada, de modo que la cantidad de overs en las dos entradas se reduce pero sigue siendo la misma entre sí, entonces D/L no cambia el puntaje objetivo, porque ambos lados conocen la cantidad total de overs y wickets a lo largo de sus entradas, por lo tanto, tendrán los mismos recursos disponibles.
- La puntuación objetivo del Equipo 2 se calcula primero una vez finalizada la entrada del Equipo 1.
- Si hubo interrupción(es) durante las entradas del Equipo 1, o las entradas del Equipo 1 se acortaron, por lo que la cantidad de overs en las dos entradas se redujo (pero aún así fueron iguales entre sí), entonces D/L ajustará la puntuación objetivo del Equipo 2 como se describió anteriormente. El ajuste al objetivo del Equipo 2 después de las interrupciones en las entradas del Equipo 1 es a menudo un aumento, lo que implica que el Equipo 2 tiene más recursos disponibles que el Equipo 1. Aunque ambos equipos tienen 10 wickets y la misma cantidad (reducida) de overs disponibles, un aumento es justo ya que, para algunas de sus entradas, el Equipo 1 pensó que tendría más overs disponibles de los que realmente terminó teniendo. Si el Equipo 1 hubiera sabido que sus entradas iban a ser más cortas, habrían bateado de manera menos conservadora y habrían anotado más carreras (a expensas de más wickets). Ahorraron algunos recursos de wicket para utilizarlos en los overs que terminaron cancelándose, algo que el Equipo 2 no necesita hacer, por lo tanto, el Equipo 2 tiene más recursos para utilizar en la misma cantidad de overs. Por lo tanto, aumentar el puntaje objetivo del Equipo 2 compensa al Equipo 1 por la negación de algunos de los overs en los que pensaban que podrían batear. El objetivo aumentado es lo que D/L cree que el Equipo 1 habría anotado en los overs que terminó teniendo, si hubiera sabido desde el principio que las entradas serían tan largas como lo fueron.
- Por ejemplo, si el Equipo 1 bateó durante 20 overs antes de que llegara la lluvia, pensando que tendrían 50 overs en total, pero al reiniciarse solo hubo tiempo para que el Equipo 2 bateara durante 20 overs, claramente sería injusto darle al Equipo 2 el objetivo que logró el Equipo 1, ya que el Equipo 1 habría bateado de manera menos conservadora y anotado más carreras si hubiera sabido que solo tendría los 20 overs.
- Si hay interrupciones en las entradas del Equipo 2, ya sea antes de que comiencen, durante o si se interrumpen, entonces D/L reducirá el puntaje objetivo del Equipo 2 del objetivo inicial establecido al final de las entradas del Equipo 1, en proporción a la reducción de los recursos del Equipo 2. Si hay múltiples interrupciones en la segunda entrada, el objetivo se ajustará hacia abajo cada vez.
- Si hay interrupciones que aumentan y disminuyen el puntaje objetivo, entonces el efecto neto sobre el objetivo podría ser un aumento o una disminución, dependiendo de qué interrupciones fueron mayores.
Teoría matemática
El modelo D/L original comenzó asumiendo que la cantidad de carreras que aún se pueden anotar (llamado ), para una cantidad dada de overs restantes (llamado ) y wickets perdidos (llamado ), toma la siguiente relación de decaimiento exponencial : [14]
donde la constante es la puntuación total media asintótica en overs ilimitados (con reglas de un día), y es la constante de decaimiento exponencial. Ambas varían con (solamente). Los valores de estos dos parámetros para cada uno de 0 a 9 se estimaron a partir de puntuaciones de "cientos de partidos internacionales de un día" y "amplia investigación y experimentación", aunque no se divulgaron debido a "confidencialidad comercial". [14]
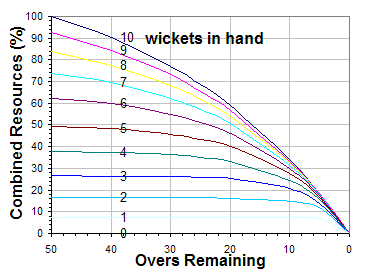
Encontrar el valor de para una combinación particular de y (poniendo y los valores de estas constantes para el ), y dividir esto por el puntaje alcanzable al comienzo de las entradas, es decir, encontrar
da la proporción de los recursos de puntuación de carreras combinados de las entradas restantes cuando quedan overs y los wickets están caídos. [14] Estas proporciones se pueden representar en un gráfico, como se muestra a la derecha, o mostrar en una sola tabla, como se muestra a continuación.
Esta se convirtió en la Edición Estándar. Cuando se introdujo, era necesario que D/L pudiera implementarse con una única tabla de porcentajes de recursos, ya que no se podía garantizar que las computadoras estuvieran presentes. Por lo tanto, se utilizó esta única fórmula que proporciona los recursos promedio. Este método se basa en el supuesto de que el rendimiento promedio es proporcional a la media, independientemente del puntaje real. Esto fue lo suficientemente bueno en el 95 por ciento de los partidos, pero en el 5 por ciento de los partidos con puntajes muy altos, el enfoque simple comenzó a fallar. [15] Para superar el problema, se propuso una fórmula mejorada con un parámetro adicional cuyo valor depende de las entradas del Equipo 1. [16] Esta se convirtió en la Edición Profesional.
Ejemplos
Paro en la primera entrada
Objetivo aumentado
En el cuarto ODI India-Inglaterra de la serie de 2008 , la primera entrada fue interrumpida por la lluvia en dos ocasiones, lo que redujo el partido a 22 overs cada una. India (bateando primero) hizo 166/4. El método D/L aumentó el objetivo de Inglaterra a 198 desde 22 overs. Como Inglaterra sabía que solo tenía 22 overs, la expectativa es que pudieran anotar más carreras de esos overs que India en sus entradas (interrumpidas). Inglaterra hizo 178/8 de 22 overs, por lo que el partido fue catalogado como "India ganó por 19 carreras (método D/L)". [17]
Durante el quinto ODI entre India y Sudáfrica en enero de 2011 , la lluvia detuvo el juego dos veces durante las primeras entradas. El partido se redujo a 46 overs cada uno. Sudáfrica anotó 250/9. El método D/L aumentó el objetivo de India a 268. Como el número de overs se redujo durante las entradas de Sudáfrica, este método tiene en cuenta lo que Sudáfrica probablemente hubiera anotado si hubiera sabido durante sus entradas que solo durarían 46 overs. El partido fue catalogado como "Sudáfrica ganó por 33 carreras (método D/L)". [18]
Objetivo disminuido
El 3 de diciembre de 2014, Sri Lanka jugó contra Inglaterra y bateó primero, pero el juego se interrumpió cuando Sri Lanka había anotado 6/1 en 2 overs. En el reinicio, ambas entradas se redujeron a 35 overs, y Sri Lanka terminó en 242/8. D/L redujo el objetivo de Inglaterra a 236 de 35 overs. [19] Aunque Sri Lanka tenía menos recursos restantes después de la interrupción de los que Inglaterra habría tenido durante todas sus entradas (alrededor de un 7% menos), habían utilizado el 8% de sus recursos (2 overs y 1 wicket) antes de la interrupción, por lo que el recurso total utilizado por Sri Lanka todavía era ligeramente mayor que el que Inglaterra tenía disponible, de ahí el objetivo ligeramente reducido para Inglaterra.
Detención en la segunda entrada
Un ejemplo sencillo de la aplicación del método D/L fue el primer ODI entre India y Pakistán en su serie ODI de 2006. [ 20] India bateó primero y quedó fuera por 328. Pakistán, bateando segundo, estaba 311/7 cuando la mala luz detuvo el juego después del 47.º over. El objetivo de Pakistán, si el partido hubiera continuado, era 18 carreras en 18 bolas, con tres wickets en la mano. Considerando la tasa de puntuación general durante todo el partido, este es un objetivo que la mayoría de los equipos estarían favorecidos a alcanzar. Y, de hecho, la aplicación del método D/L resultó en un puntaje objetivo retrospectivo de 305 (o puntaje par de 304) al final del 47.º over, con el resultado, por lo tanto, oficialmente listado como " Pakistán ganó por 7 carreras (Método D/L)".
El método D/L se utilizó en el partido de la fase de grupos entre Sri Lanka y Zimbabwe en la Copa del Mundo T20 de 2010. Sri Lanka anotó 173/7 en 20 overs bateando primero, y en respuesta Zimbabwe estaba 4/0 desde 1 over cuando la lluvia interrumpió el juego. En el reinicio, el objetivo de Zimbabwe se redujo a 108 desde 12 overs, pero la lluvia detuvo el partido cuando habían anotado 29/1 desde 5 overs. El objetivo D/L retrospectivo desde 5 overs fue una reducción adicional a 44, o un puntaje par de 43, y por lo tanto Sri Lanka ganó el partido por 14 carreras. [21] [22]
El método DLS también se utilizó después de la interrupción por lluvia en la final de la Indian Premier League de 2023 , cuando Chennai Super Kings había anotado 4/0 (0,3 overs) y los Gujarat Titans acababan de anotar 214/4 (20 overs). El objetivo se redujo a 171 carreras en 15 overs del objetivo anterior de 215 carreras en 20 overs para Chennai Super Kings. Chennai Super Kings ganó por 5 wickets con el método DLS. Esto se logró al llegar a 171/5 en 15 overs.
Un ejemplo de un partido empatado con empate a D/L fue el ODI entre Inglaterra e India el 11 de septiembre de 2011. Este partido fue interrumpido frecuentemente por la lluvia en los overs finales, y un cálculo bola por bola del puntaje "par" de Duckworth-Lewis jugó un papel clave en las decisiones tácticas durante esos overs. En un momento, India estaba liderando bajo D/L durante una demora por lluvia, y habría ganado si el juego no se hubiera reanudado. En un segundo intervalo por lluvia, Inglaterra, que había anotado algunas carreras rápidas (sabiendo que necesitaban ponerse por delante en términos de D/L) correspondientemente habría ganado si el juego no se hubiera reanudado. El juego finalmente se suspendió con solo 7 bolas restantes del partido y el puntaje de Inglaterra igual al puntaje "par" de Duckworth-Lewis, por lo tanto, resultó en un empate.
Este ejemplo muestra lo cruciales (y difíciles) que pueden ser las decisiones de los árbitros a la hora de evaluar cuándo la lluvia es lo suficientemente intensa como para justificar la interrupción del juego. Si los árbitros de ese partido hubieran detenido el juego una bola antes, Inglaterra habría estado por delante en D/L y, por lo tanto, habría ganado el partido. Del mismo modo, si el juego se hubiera detenido una bola más tarde, India podría haber ganado el partido con una bola sin efecto , lo que indica lo precisos que pueden ser los cálculos de D/L en tales situaciones.
Paros en ambas entradas
Durante la KFC Big Bash League 2012/13 , se utilizó D/L en la segunda semifinal jugada entre Melbourne Stars y Perth Scorchers . Después de que la lluvia retrasara el inicio del partido, interrumpió las entradas de Melbourne cuando habían anotado 159/1 en 15.2 overs, y ambas entradas se redujeron en 2 overs a 18, y Melbourne terminó en 183/2. Después de que una nueva demora por lluvia redujera las entradas de Perth a 17 overs, Perth regresó al campo para enfrentar 13 overs, con un objetivo revisado de 139. Perth ganó el juego por 8 wickets con un límite en la bola final. [23] [24]
Uso y actualizaciones
La tabla publicada que sustenta el método D/L se actualiza periódicamente, utilizando datos fuente de los partidos más recientes; esto se hace el 1 de julio de cada año. [25]
Para los partidos de 50 overs decididos por D/L, cada equipo debe enfrentar al menos 20 overs para que el resultado sea válido, y para los juegos Twenty20 decididos por D/L, cada lado debe enfrentar al menos cinco overs, a menos que uno o ambos equipos sean eliminados y/o el segundo equipo alcance su objetivo en menos overs.
Si las condiciones impiden que un partido alcance esta duración mínima, se declara sin resultado .
1996–2003 – Versión individual
Hasta 2003, se utilizó una única versión de D/L. Esta utilizaba una única tabla de referencia publicada de porcentajes totales de recursos restantes para todas las combinaciones posibles de overs y wickets [26] y algunos cálculos matemáticos simples , y era relativamente transparente y sencilla de implementar.
Sin embargo, una falla en la forma en que manejaba las puntuaciones muy altas en la primera entrada (350+) se hizo evidente a partir del partido de la Copa Mundial de Cricket de 1999 en Bristol entre India y Kenia. Tony Lewis notó que había una debilidad inherente en la fórmula que daría una ventaja notable al equipo que persiguiera un total superior a 350. Se incorporó una corrección a la fórmula y al software, pero no se adoptó por completo hasta 2004. Los partidos de un día estaban logrando puntuaciones significativamente más altas que en décadas anteriores, lo que afectaba la relación histórica entre recursos y carreras. La segunda versión utiliza un modelo estadístico más sofisticado, pero no utiliza una sola tabla de porcentajes de recursos. En cambio, los porcentajes también varían con la puntuación, por lo que se requiere una computadora. [13] Por lo tanto, pierde algunas de las ventajas anteriores de transparencia y simplicidad.
En 2002, los porcentajes de recursos fueron revisados, luego de un análisis exhaustivo de partidos con overs limitados, y hubo un cambio en el G50 para los ODI. (G50 es el puntaje promedio esperado del equipo que batea primero en un partido ininterrumpido de 50 overs por entrada). G50 se cambió a 235 para los ODI. Estos cambios entraron en vigencia el 1 de septiembre de 2002. [27] A partir de 2014, estos porcentajes de recursos son los que todavía se usan en la Edición estándar, aunque G50 ha cambiado posteriormente.
Las tablas muestran cómo eran los porcentajes en 1999 y 2001, y cómo se modificaron en 2002. En su mayoría se redujeron.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2004 – Adopción de la segunda versión
La versión original se llamó Standard Edition y la nueva versión se llamó Professional Edition. Tony Lewis dijo: "En ese momento [en el momento de la final de la Copa del Mundo de 2003 ] estábamos usando lo que ahora se conoce como Standard Edition. ... Australia obtuvo 359 y eso mostró los defectos e inmediatamente se introdujo la siguiente edición, que manejaba las puntuaciones altas mucho mejor. Es probable que la puntuación par para India sea mucho más alta ahora". [30]
Duckworth y Lewis escribieron: "Cuando el equipo que batea primero tiene una puntuación igual o inferior a la media del cricket de alto nivel..., los resultados de aplicar la Edición Profesional son generalmente similares a los de la Edición Estándar. Para partidos con puntuaciones más altas, los resultados comienzan a divergir y la diferencia aumenta cuanto mayor sea el total de la primera entrada. En efecto, ahora hay una tabla diferente de porcentajes de recursos para cada puntuación total en las entradas del Equipo 1". [13] La Edición Profesional se ha utilizado en todos los partidos internacionales de cricket de un día desde principios de 2004. Esta edición también eliminó el uso de la constante G50 al lidiar con interrupciones en las primeras entradas. [13]
La decisión sobre qué edición se debe utilizar corresponde a la autoridad de cricket que organiza la competición en particular. [13] El Manual de Juego de la ICC exige el uso de la Edición Profesional para los partidos internacionales. [31] [32] Esto también se aplica a las competiciones nacionales de la mayoría de los países. [13] En los niveles inferiores del juego, donde no siempre se puede garantizar el uso de una computadora, se utiliza la Edición Estándar. [13]
2009 - Actualizaciones de Twenty20
En junio de 2009, se informó que el método D/L sería revisado para el formato Twenty20 después de que se cuestionara su idoneidad en la versión más rápida del juego. Lewis admitió que "sin duda, la gente ha sugerido que debemos analizar con mucho cuidado y ver si, de hecho, los números de nuestra fórmula son totalmente apropiados para el juego Twenty20". [33]
2015 – Se convierte en DLS
Para la Copa Mundial de 2015 , el ICC implementó la fórmula Duckworth-Lewis-Stern, que incluyó el trabajo del nuevo custodio del método, el profesor Steven Stern , del Departamento de Estadística de la Universidad Tecnológica de Queensland . Estos cambios reconocieron que los equipos necesitan comenzar con una tasa de puntuación más alta cuando persiguen objetivos altos en lugar de mantener los wickets en la mano. [34]
Cálculos de puntuación objetivo
Usando la notación del Manual de Juego del ICC, [32] el equipo que batea primero se llama Equipo 1, su puntaje final se llama S, los recursos totales disponibles para el Equipo 1 para sus entradas se llaman R1, el equipo que batea segundo se llama Equipo 2, y los recursos totales disponibles para el Equipo 2 para sus entradas se llaman R2.
| Overs restantes | Portillos en mano | ||||
|---|---|---|---|---|---|
| 10 | 8 | 6 | 4 | 2 | |
| 50 | 100.0 | 85.1 | 62,7 | 34.9 | 11.9 |
| 40 | 89.3 | 77.8 | 59,5 | 34.6 | 11.9 |
| 30 | 75.1 | 67.3 | 54.1 | 33.6 | 11.9 |
| 20 | 56.6 | 52.4 | 44.6 | 30.8 | 11.9 |
| 10 | 32.1 | 30.8 | 28.3 | 22.8 | 11.4 |
| 5 | 17.2 | 16.8 | 16.1 | 14.3 | 9.4 |
Paso 1. Encuentra los recursos de bateo disponibles para cada equipo
Después de cada reducción en overs, se calculan los nuevos recursos totales de bateo disponibles para los dos equipos, utilizando cifras para la cantidad total de recursos de bateo restantes para cualquier combinación de overs y wickets. Si bien el proceso para convertir estas cifras de recursos restantes en cifras de recursos totales disponibles es el mismo en las dos ediciones, esto se puede hacer manualmente en la Edición estándar, ya que las cifras de recursos restantes se publican en una tabla de referencia. [26] Sin embargo, las cifras de recursos restantes utilizadas en la Edición profesional no están disponibles públicamente, [13] por lo que se debe utilizar una computadora que tenga cargado el software.
- Si un equipo pierde un recurso al comienzo de una entrada (imagen de la izquierda a continuación), esto es simple. Por ejemplo, si se pierden los primeros 20 overs de una entrada, entonces quedan 30 overs y 10 wickets, lo que representa el 75,1 % en la Edición estándar, por lo que este es el recurso disponible.
- Si un equipo pierde un recurso al final de sus entradas (imagen central a continuación), entonces el recurso que estaba disponible para ese equipo se encuentra tomando los recursos que tenía al comienzo y restando los recursos que quedaban al momento en que terminó la entrada. Por ejemplo, si un equipo comienza con 50 overs y 10 wickets (100% de sus recursos), pero su entrada termina con 20 overs y 8 wickets restantes (52,4% de sus recursos), entonces los recursos que realmente utilizó son 100% − 52,4% = 47,6%.
- Si un equipo pierde un recurso en medio de sus entradas (imagen de la derecha a continuación), entonces el recurso que estaba disponible para ese equipo se encuentra tomando los recursos que tenía al comienzo y restando los recursos restantes en el momento en que se interrumpió la entrada (para obtener los recursos utilizados en el primer período de las entradas), luego agregando el recurso restante en el reinicio. Por ejemplo, si un equipo comienza con 50 overs y 10 wickets (100% de sus recursos), pero se interrumpe cuando todavía tiene 40 overs y 8 wickets restantes (77.8% de sus recursos), y reinicia cuando tiene 20 overs y 8 wickets restantes (52.4% de sus recursos), entonces los recursos que realmente utilizó son 100% − 77.8% + 52.4% = 74.6%. Otra forma de ver esto es decir que perdió los recursos disponibles entre 40 overs y 8 wickets (77,8%) y 20 overs y 8 wickets (52,4%), es decir, 77,8% − 52,4% = 25,4%, por lo que su recurso total disponible fue 100% − 25,4% = 74,6%.
Estas son solo las diferentes formas de tener una interrupción. Con múltiples interrupciones posibles, puede parecer que encontrar el porcentaje total de recursos requiere un cálculo diferente para cada escenario diferente. Sin embargo, la fórmula es en realidad la misma cada vez, es solo que los diferentes escenarios, con más o menos interrupciones y reinicios, necesitan usar más o menos la misma fórmula. Los recursos totales disponibles para un equipo están dados por: [26]
| Recursos totales disponibles = 100% − ( Recursos perdidos por la 1.ª interrupción ) − ( Recursos perdidos por la 2.ª interrupción ) − ( Recursos perdidos por la 3.ª interrupción ) − ... |
que alternativamente puede escribirse como:
| Recursos totales disponibles = 100% − Recursos restantes en la 1.ª interrupción + Recursos restantes en el 1.er reinicio − Recursos restantes en la 2.ª interrupción + Recursos restantes en el 2.º reinicio − Recursos restantes en la 3.ª interrupción + Recursos restantes en el 3.er reinicio − ... |
Cada vez que se produce una interrupción o un reinicio después de una interrupción, se pueden introducir en la fórmula los porcentajes de recursos restantes en esos momentos (obtenidos de una tabla de referencia para la Edición estándar o de una computadora para la Edición profesional), dejando el resto en blanco. Tenga en cuenta que una demora al comienzo de una entrada cuenta como la primera interrupción.
Paso 2. Convierte los recursos de bateo de los dos equipos en el puntaje objetivo del Equipo 2
Edición estándar
- Si R2 < R1, reduce la puntuación objetivo del Equipo 2 en proporción a la reducción de los recursos totales, es decir, S × R2/R1 .
- Si R2 = R1, no es necesario realizar ningún ajuste en la puntuación objetivo del Equipo 2.
- Si R2 > R1, aumenta el puntaje objetivo del Equipo 2 por las carreras adicionales que se podrían esperar anotar en promedio con el recurso total adicional, es decir, S + G50 × (R2 – R1)/100 , donde G50 es el total promedio de 50 overs. El puntaje objetivo del Equipo 2 no se incrementa simplemente en proporción al aumento en los recursos totales, es decir, S × R2/R1, ya que esto "podría llevar a algunos objetivos irrealmente altos si el Equipo 1 hubiera logrado una alta tasa temprana de puntuación [en los overs de powerplay ] y la lluvia causara una reducción drástica en los overs del partido". [13] En cambio, D/L Standard Edition requiere un rendimiento promedio para el recurso adicional del Equipo 2 sobre el Equipo 1.
G50
G50 es el puntaje promedio esperado del equipo que batea primero en un partido ininterrumpido de 50 overs por entrada. Esto variará según el nivel de competencia y con el tiempo. El Manual de Juego anual de la ICC [32] proporciona los valores de G50 que se deben usar cada año cuando se aplica la Edición Estándar D/L:
| Período | Partidos en los que participan países miembros plenos de la ICC | Partidos entre equipos que juegan al cricket de primera clase. | Internacionales sub-19 | Internacionales sub-15 | Partidos entre los países miembros asociados de la CPI | ODI femeninos |
| 1999 − 31 de agosto de 2002 [35] | 225 | ? | ||||
| 1 de septiembre de 2002 − 2006 [27] | 235 | |||||
| 2006/07 [36] | 235 | 200 | 190 | 175 | ||
| 2007/08 | ||||||
| 2008/09 [32] | ||||||
| 2009/10 [32] | 245 | 200 | ||||
| 2010/11 [32] | ||||||
| 2011/12 [32] | ||||||
| 2012/13 [32] | ||||||
| 2013/14 [32] | ||||||
Duckworth y Lewis escribieron:
Aceptamos que el valor de G50, tal vez, debería ser diferente para cada país, o incluso para cada campo, y no hay razón por la cual cualquier autoridad de cricket no pueda elegir el valor que crea más apropiado. De hecho, sería posible que los dos capitanes acordaran un valor de G50 antes del comienzo de cada partido, teniendo en cuenta todos los factores relevantes. Sin embargo, no creemos que algo que solo se invoca si la lluvia interfiere con el juego deba imponerse en todos los partidos de esta manera. En cualquier caso, debe tenerse en cuenta que el valor de G50 generalmente tiene muy poco efecto en el objetivo revisado. Si se usara 250, por ejemplo, en lugar de 235, es poco probable que el objetivo fuera más de dos o tres carreras diferente. [13]
Edición profesional
- Si R2 < R1, reduce la puntuación objetivo del Equipo 2 en proporción a la reducción de los recursos totales, es decir, S × R2/R1 .
- Si R2 = R1, no es necesario realizar ningún ajuste en la puntuación objetivo del Equipo 2.
- Si R2 > R1, aumenta el puntaje objetivo del Equipo 2 en proporción al aumento en los recursos totales, es decir, S × R2/R1 . El problema de las altas tasas de puntaje iniciales que potencialmente producen objetivos anómalamente altos se ha superado en la Edición Profesional, que es esencialmente "una tabla diferente de porcentajes de recursos para cada puntaje total en las entradas del Equipo 1". [13] Por lo tanto, el puntaje objetivo del Equipo 2 se puede aumentar simplemente en proporción al aumento en los recursos totales cuando R2 > R1, [13] y no hay G50.
Ejemplo de cálculos de puntuación objetivo de la edición estándar
Como los porcentajes de recursos utilizados en la Edición Profesional no están disponibles públicamente, es difícil dar ejemplos del cálculo de D/L para la Edición Profesional. Por lo tanto, se dan ejemplos de cuando la Edición Estándar era ampliamente utilizada, es decir, hasta principios de 2004.
Objetivo reducido: entradas del Equipo 1 completadas; entradas del Equipo 2 retrasadas (recursos perdidos al inicio de las entradas)
| Overs restantes | Portillos en mano | ||||
|---|---|---|---|---|---|
| 10 | 8 | 6 | 4 | 2 | |
| 31 | 76,7 | 68.6 | 54.8 | 33.7 | 11.9 |
| 30 | 75.1 | 67.3 | 54.1 | 33.6 | 11.9 |
| 29 | 73.5 | 66.1 | 53.4 | 33.4 | 11.9 |
| 28 | 71.8 | 64.8 | 52.6 | 33.2 | 11.9 |
| 27 | 70.1 | 63.4 | 51.8 | 33.0 | 11.9 |
El 18 de mayo de 2003, Lancashire jugó contra Hampshire en la Liga Nacional ECB de 2003. [37] [38] [39] La lluvia antes del juego redujo el partido a 30 overs cada uno. Lancashire bateó primero y anotó 231–4 en sus 30 overs. Antes de que Hampshire comenzara sus entradas, se redujo aún más a 28 overs.
| Paso 1 | Recursos totales disponibles para Lancashire (R1) | 30 overs y 10 wickets | 75,1% |
| Recursos totales disponibles para Hampshire (R2) | 28 overs y 10 wickets | 71,8% | |
| Paso 2 | Puntuación par de Hampshire | 231 x R2/R1 = 231 x 71,8/75,1 | 220.850 carreras |
Por lo tanto, el objetivo de Hampshire era 221 para ganar (en 28 overs) o 220 para empatar. Todos quedaron fuera por 150, lo que le dio la victoria a Lancashire por 220 − 150 = 70 carreras.
Si el objetivo de Hampshire se hubiera establecido con el método de tasa de carreras promedio (simplemente en proporción a la reducción de overs), su puntuación par habría sido 231 x 28/30 = 215,6, lo que daría 216 para ganar o 215 para empatar. Si bien esto habría mantenido la tasa de carreras requerida igual a la lograda por Lancashire (7,7 carreras por over), esto le habría dado una ventaja injusta a Hampshire, ya que es más fácil lograr y mantener una tasa de carreras durante un período más corto. Aumentar el objetivo de Hampshire de 216 supera esta falla.
Como las entradas de Lancashire se interrumpieron una vez (antes de comenzar) y luego se reiniciaron, su recurso se puede encontrar a partir de la fórmula general anterior de la siguiente manera (la de Hampshire es similar): Recursos totales = 100% − Recursos restantes en la 1.ª interrupción + Recursos restantes en el 1.er reinicio = 100% − 100% + 75,1% = 75,1%.
Objetivo reducido: entradas del Equipo 1 completadas; entradas del Equipo 2 acortadas (recursos perdidos al final de las entradas)
| Overs restantes | Portillos en mano | ||||
|---|---|---|---|---|---|
| 10 | 8 | 6 | 4 | 2 | |
| 50 | 100.0 | 85.1 | 62,7 | 34.9 | 11.9 |
| 40 | 89.3 | 77.8 | 59,5 | 34.6 | 11.9 |
| 30 | 75.1 | 67.3 | 54.1 | 33.6 | 11.9 |
| 20 | 56.6 | 52.4 | 44.6 | 30.8 | 11.9 |
| 10 | 32.1 | 30.8 | 28.3 | 22.8 | 11.4 |
| 5 | 17.2 | 16.8 | 16.1 | 14.3 | 9.4 |
El 3 de marzo de 2003, Sri Lanka jugó contra Sudáfrica en el Grupo B de la Copa del Mundo . [40] [41] Sri Lanka bateó primero y anotó 268–9 en sus 50 overs. Persiguiendo un objetivo de 269, Sudáfrica había llegado a 229–6 en 45 overs cuando se abandonó el juego.
| Paso 1 | Total de recursos disponibles para Sri Lanka (R1) | 50 overs y 10 wickets | 100.0% |
| Recursos totales disponibles para Sudáfrica al inicio de sus entradas | 50 overs y 10 wickets | 100.0% | |
| Total de recursos que le quedaban a Sudáfrica cuando se abandonó el juego | 5 overs y 4 wickets | 14,3% | |
| Recursos totales disponibles para Sudáfrica (R2) | 100,0% − 14,3% | 85,7% | |
| Paso 2 | Puntuación par de Sudáfrica | 268 × R2/R1 = 268 × 85,7/100,0 | 229.676 carreras |
Por lo tanto, el objetivo retrospectivo de Sudáfrica en sus 45 overs era 230 carreras para ganar, o 229 para empatar. En ese caso, como habían anotado exactamente 229, el partido se declaró empatado.
Sudáfrica no anotó ninguna carrera con la última bola. Si el juego se hubiera abandonado sin que se hubiera lanzado esa bola, el recurso disponible para Sudáfrica en el momento del abandono habría sido del 14,7%, lo que le habría dado un puntaje par de 228,6 y, por lo tanto, la victoria.
Como las entradas de Sudáfrica se interrumpieron una vez (y no se reiniciaron), su recurso se da por la fórmula general anterior de la siguiente manera: Recursos totales disponibles = 100% − Recursos restantes en la primera interrupción = 100% − 14,3% = 85,7%.
Objetivo reducido: entradas del Equipo 1 completadas; entradas del Equipo 2 interrumpidas (recursos perdidos en mitad de las entradas)
El 16 de febrero de 2003, Nueva Gales del Sur jugó contra Australia del Sur en la Copa ING. [42] [43] Nueva Gales del Sur bateó primero y anotó 273 (en 49,4 overs). Persiguiendo un objetivo de 274, la lluvia interrumpió el juego cuando Australia del Sur había alcanzado 70-2 en 19 overs, y en el reinicio sus entradas se redujeron a 36 overs (es decir, 17 restantes).
| Paso 1 | Recursos totales disponibles para Nueva Gales del Sur (R1) | 50 overs y 10 wickets | 100.0% |
| Recursos totales disponibles para Australia del Sur al inicio de sus entradas | 50 overs y 10 wickets | 100.0% | |
| Recursos totales que le quedan a Australia del Sur en el momento de la interrupción | 31 overs y 8 wickets | 68,6% | |
| Recursos totales que quedan en Australia del Sur al reiniciarse | 17 overs y 8 wickets | 46,7% | |
| Recursos totales perdidos en Australia del Sur por la interrupción | 68,6% - 46,7% | 21,9% | |
| Recursos totales disponibles para Australia del Sur (R2) | 100,0% − 21,9% | 78,1% | |
| Paso 2 | Puntuación par de Australia del Sur | 273 × R2/R1 = 273 × 78,1/100,0 | 213.213 carreras |
El nuevo objetivo de Australia del Sur era, por tanto, 214 para ganar (en 36 overs) o 213 para empatar. Al final, todos quedaron fuera por 174, por lo que Nueva Gales del Sur ganó por 213 - 174 = 39 carreras.
Como las entradas de Australia del Sur se interrumpieron una vez y se reiniciaron una vez, su recurso se da por la fórmula general anterior de la siguiente manera: Recursos totales disponibles = 100% − Recursos restantes en la 1.ª interrupción + Recursos restantes en el 1.er reinicio = 100% − 68,6% + 46,7% = 78,1%.
Objetivo aumentado: las entradas del Equipo 1 se acortaron (recursos perdidos al final de las entradas); las entradas del Equipo 2 se completaron
El 25 de enero de 2001, las Indias Occidentales jugaron contra Zimbabue . [44] [45] Las Indias Occidentales batearon primero y habían alcanzado 235-6 en 47 overs (de los 50 programados) cuando la lluvia detuvo el juego durante dos horas. En el reinicio, ambas entradas se redujeron a 47 overs, es decir, las entradas de las Indias Occidentales se cerraron inmediatamente y Zimbabue comenzó sus entradas.
| Paso 1 | Recursos totales disponibles para las Indias Occidentales al inicio de sus entradas | 50 overs y 10 wickets | 100.0% |
| Total de recursos que le quedaban a las Indias Occidentales cuando se cerraron las entradas | 3 overs y 4 wickets | 10,2% | |
| Recursos totales disponibles para las Indias Occidentales (R1) | 100,0% − 10,2% | 89,8% | |
| Recursos totales disponibles para Zimbabwe (R2) | 47 overs y 10 wickets | 97,4% | |
| Paso 2 | Puntuación par de Zimbabwe | 235 + G50 × (R2 − R1)/100 = 235 + 225 × (97,4 − 89,8)/100 | 252.100 carreras |
Por lo tanto, el objetivo de Zimbabwe era 253 para ganar (en 47 overs), o 252 para empatar. Es justo que su objetivo se haya incrementado, a pesar de que tenían el mismo número de overs para batear que West Indies, ya que West Indies habría bateado de manera más agresiva en sus últimos overs y habría anotado más carreras si hubiera sabido que sus entradas se acortarían en 47 overs. Zimbabwe fue eliminado por 175, lo que le dio la victoria a West Indies por 252 − 175 = 77 carreras.
Estos porcentajes de recursos son los que se usaban en 2001, antes de la revisión de 2002, y por lo tanto no coinciden con los porcentajes que se usan actualmente para la Edición Estándar, que son ligeramente diferentes. Además, la fórmula para la puntuación par de Zimbabue proviene de la Edición Estándar de D/L, que se usaba en ese momento. Actualmente se usa la Edición Profesional, que tiene una fórmula diferente cuando R2>R1. La fórmula requería que Zimbabue igualara el desempeño de las Indias Occidentales con su superposición del 89,8% de recursos (es decir, anotara 235 carreras) y lograra un desempeño promedio con su 97,4% adicional − 89,8% = 7,6% de recursos (es decir, anotara el 7,6% de G50 (225 en ese momento) = 17,1 carreras).
Como las entradas de las Indias Occidentales se interrumpieron una vez (y no se reiniciaron), su recurso se da por la fórmula general anterior de la siguiente manera: Recursos totales disponibles = 100% − Recursos restantes en la primera interrupción = 100% − 10,2% = 89,8%.
Objetivo aumentado: Múltiples interrupciones en las entradas del Equipo 1 (recursos perdidos en mitad de las entradas); entradas del Equipo 2 completadas
El 20 de febrero de 2003, Australia jugó contra los Países Bajos en el Grupo A de la Copa Mundial de Críquet de 2003. [ 46] [47] [48] [49] La lluvia antes del juego redujo el partido a 47 overs cada uno, y Australia bateó primero.
- La lluvia detuvo el juego cuando habían alcanzado el 109-2 en 25 overs (es decir, quedaban 22). En el reinicio, ambas entradas se redujeron a 44 overs (es decir, quedaban 19 para Australia).
- La lluvia detuvo el juego nuevamente cuando Australia había alcanzado 123-2 en 28 overs (es decir, 16 restantes), y en el reinicio ambas entradas se redujeron aún más a 36 overs (es decir, 8 restantes para Australia).
- Australia terminó con 170-2 en sus 36 overs.
| Paso 1 | Recursos totales disponibles para Australia al inicio de sus entradas | 47 overs y 10 wickets | 97,1% |
| Total de recursos que le quedan a Australia en el momento de la interrupción | 22 overs y 8 wickets | 55,8% | |
| Total de recursos que le quedan a Australia al reiniciarse | 19 overs y 8 wickets | 50,5% | |
| Total de recursos perdidos por interrupción | 55,8% - 50,5% | 5,3% | |
| Total de recursos que le quedan a Australia en el momento de la interrupción | 16 overs y 8 wickets | 44,7% | |
| Total de recursos que le quedan a Australia al reiniciarse | 8 overs y 8 wickets | 25,5% | |
| Total de recursos perdidos por interrupción | 44,7% - 25,5% | 19,2% | |
| Recursos totales disponibles para Australia (R1) | 97,1% - 5,3% - 19,2% | 72,6% | |
| Recursos totales disponibles para los Países Bajos (R2) | 36 overs y 10 wickets | 84,1% | |
| Paso 2 | Puntuación par de los Países Bajos | 170 + G50 × (R2 − R1)/100 = 170 + 235 × (84,1 − 72,6)/100 | 197.025 carreras |
Por lo tanto, el objetivo de Holanda era 198 para ganar (en 36 overs), o 197 para empatar. Es justo que su objetivo se haya incrementado, a pesar de que tenían el mismo número de overs para batear que Australia, ya que Australia habría bateado de manera menos conservadora en sus primeros 28 overs y habría anotado más carreras a expensas de más wickets, si hubiera sabido que sus entradas solo durarían 36 overs. Aumentar el puntaje objetivo de Holanda neutraliza la injusticia cometida con Australia cuando se le negaron algunos de los overs para batear que pensaban que obtendrían. Holanda quedó fuera por 122, lo que le dio la victoria a Australia por 197 − 122 = 75 carreras.
Esta fórmula para la puntuación par de los Países Bajos proviene de la Edición estándar de D/L, que se utilizaba en ese momento. Actualmente se utiliza la Edición profesional, que tiene una fórmula diferente cuando R2>R1. La fórmula requería que los Países Bajos igualaran el rendimiento de Australia con su 72,6 % superpuesto de recursos (es decir, lograran 170 carreras) y lograran un rendimiento promedio con su 84,1 % adicional − 72,6 % = 11,5 % de recursos (es decir, lograran un 11,5 % de G50 (235 en ese momento) = 27,025 carreras).
Después del partido hubo informes en los medios [47] de que Australia había bateado de manera conservadora en sus últimos 8 overs después del reinicio final, para evitar perder wickets en lugar de maximizar sus números de carreras, en la creencia de que esto aumentaría aún más el puntaje par de los Países Bajos. Sin embargo, si esto es cierto, esta creencia fue errónea, de la misma manera que conservar wickets en lugar de maximizar las carreras en los últimos 8 overs de una entrada completa de 50 overs sería un error. En ese momento, la cantidad de recursos disponibles para cada equipo era fija (siempre que no hubiera más interrupciones por lluvia), por lo que el único número indeterminado en la fórmula para el puntaje par de los Países Bajos era el puntaje final de Australia, por lo que deberían haber tratado de maximizarlo.
Como las entradas de Australia se interrumpieron tres veces (una antes de comenzar) y se reiniciaron tres veces, su recurso está dado por la fórmula general anterior de la siguiente manera:
Recursos totales disponibles = 100% − Recursos restantes en la 1.ª interrupción + Recursos restantes en el 1.er reinicio − Recursos restantes en la 2.ª interrupción + Recursos restantes en el 2.º reinicio − Recursos restantes en la 3.ª interrupción + Recursos restantes en el 3.er reinicio = 100% − 100% + 97,1% − 55,8% + 50,5% − 44,7% + 25,5% = 72,6%.
Estrategia en el juego
Durante las entradas del equipo 1
Estrategia para el equipo 1
Durante las entradas del Equipo 1, los cálculos del puntaje objetivo (como se describe arriba) aún no se han realizado.
El objetivo del equipo que batea primero es maximizar la puntuación objetivo que se calculará para el equipo que batea segundo, que (en la Edición Profesional) se determinará mediante la fórmula:
Para estos tres términos:
- Puntuación del equipo 1 : el equipo 1 siempre aumentará el objetivo del equipo 2 aumentando su propia puntuación.
- Al comienzo de las entradas del Equipo 2, los recursos del Equipo 2 serán 10 wickets y la cantidad de overs disponibles, y el Equipo 1 no puede afectar esto.
- Los recursos del equipo 1 están dados por:
| Recursos totales disponibles = 100% − Recursos perdidos por la 1.ª interrupción − Recursos perdidos por la 2.ª interrupción − Recursos perdidos por la 3.ª interrupción − ... |
Si no habrá interrupciones futuras en las entradas del Equipo 1, entonces la cantidad de recursos disponibles para ellos ahora es fija (ya sea que haya habido interrupciones hasta ahora o no), por lo que lo único que el Equipo 1 puede hacer para aumentar el objetivo del Equipo 2 es aumentar su propio puntaje, ignorando cuántos wickets pierden (como en un partido normal no afectado).
Sin embargo, si en el futuro se producen interrupciones en las entradas del Equipo 1, una estrategia alternativa para anotar más carreras es minimizar la cantidad de recursos que utilizan antes de la próxima interrupción (es decir, preservar los wickets). Si bien la mejor estrategia general es, obviamente, anotar más carreras y preservar los recursos, si se debe elegir entre las dos, a veces preservar los wickets a expensas de anotar carreras (bateo "conservador") es una forma más efectiva de aumentar el objetivo del Equipo 2, y a veces ocurre lo contrario (bateo "agresivo").
| Overs restantes | Portillos en mano | ||||
|---|---|---|---|---|---|
| 10 | 8 | 6 | 4 | 2 | |
| 50 | 100.0 | 85.1 | 62,7 | 34.9 | 11.9 |
| 40 | 89.3 | 77.8 | 59,5 | 34.6 | 11.9 |
| 30 | 75.1 | 67.3 | 54.1 | 33.6 | 11.9 |
| 20 | 56.6 | 52.4 | 44.6 | 30.8 | 11.9 |
| 10 | 32.1 | 30.8 | 28.3 | 22.8 | 11.4 |
| 5 | 17.2 | 16.8 | 16.1 | 14.3 | 9.4 |
Por ejemplo, supongamos que el Equipo 1 ha estado bateando sin interrupciones, pero cree que las entradas se acortarán en 40 overs, es decir, con 10 overs restantes. (Entonces el Equipo 2 tendrá 40 overs para batear, por lo que el recurso del Equipo 2 será del 89,3%.) El Equipo 1 cree que al batear de manera conservadora puede llegar a 200-6, o al batear agresivamente puede llegar a 220-8:
| Estrategia de bateo | Conservador | Agresivo |
| El equipo 1 cree que puede anotar | 200 | 220 |
| El equipo 1 de Wickets cree que tendrá en la mano | 4 | 2 |
| Recurso restante para el Equipo 1 en el corte | 22,8% | 11,4% |
| Recurso utilizado por el equipo 1 | 100% - 22,8% = 77,2% | 100% - 11,4% = 88,6% |
| Puntuación par del equipo 2 | 200 + 250 x (89,3% - 77,2%) = 230,25 carreras | 220 + 250 x (89,3% - 88,6%) = 221,75 carreras |
Por lo tanto, en este caso, la estrategia conservadora logra un objetivo más alto para el Equipo 2.
| Overs restantes | Portillos en mano | ||||
|---|---|---|---|---|---|
| 10 | 8 | 6 | 4 | 2 | |
| 50 | 100.0 | 85.1 | 62,7 | 34.9 | 11.9 |
| 40 | 89.3 | 77.8 | 59,5 | 34.6 | 11.9 |
| 30 | 75.1 | 67.3 | 54.1 | 33.6 | 11.9 |
| 20 | 56.6 | 52.4 | 44.6 | 30.8 | 11.9 |
| 10 | 32.1 | 30.8 | 28.3 | 22.8 | 11.4 |
| 5 | 17.2 | 16.8 | 16.1 | 14.3 | 9.4 |
Sin embargo, supongamos que la diferencia entre las dos estrategias es 200-2 o 220-4:
| Estrategia de bateo | Conservador | Agresivo |
| El equipo 1 cree que puede anotar | 200 | 220 |
| El equipo 1 de Wickets cree que tendrá en la mano | 8 | 6 |
| Recurso restante para el Equipo 1 en el corte | 30,8% | 28,3% |
| Recurso utilizado por el equipo 1 | 100% - 30,8% = 69,2% | 100% - 28,3% = 71,7% |
| Puntuación par del equipo 2 | 200 + 250 x (89,3% - 69,2%) = 250,25 carreras | 220 + 250 x (89,3% - 71,7%) = 264,00 carreras |
En este caso, la estrategia agresiva es mejor.
Por lo tanto, la mejor estrategia de bateo para el Equipo 1 antes de una interrupción venidera no siempre es la misma, sino que varía con los hechos de la situación del partido hasta la fecha (carreras anotadas, wickets perdidos, overs utilizados y si ha habido interrupciones), y también con las opiniones sobre lo que sucederá con cada estrategia (¿cuántas carreras más se anotarán, más wickets se perderán y más overs se utilizarán? ¿Qué probabilidad hay de que se produzcan las próximas interrupciones, cuándo ocurrirán y cuánto durarán? ¿Se reiniciarán las entradas del Equipo 1?).
Este ejemplo muestra sólo dos posibles estrategias de bateo, pero en realidad podría haber una variedad de otras, por ejemplo, "neutral", "semi-agresiva", "super-agresiva" o pérdida de tiempo para minimizar la cantidad de recursos utilizados al reducir la tasa de overs. Para determinar qué estrategia es la mejor, sólo es posible introducir los hechos y las opiniones de uno en los cálculos y ver qué surge.
Por supuesto, una estrategia elegida puede resultar contraproducente. Por ejemplo, si el Equipo 1 decide batear de manera conservadora, el Equipo 2 puede darse cuenta de ello y decidir atacar (en lugar de centrarse en salvar carreras), y el Equipo 1 puede no anotar muchas más carreras y perder wickets.
Si ya ha habido interrupciones en las entradas del Equipo 1, el cálculo del total de recursos que utilizan será más complicado que en este ejemplo.
Estrategia para el equipo 2
Durante las entradas del Equipo 1, el objetivo del Equipo 2 es minimizar el puntaje objetivo que se les asignará. Esto se logra minimizando el puntaje del Equipo 1 o (como se indicó anteriormente), si habrá interrupciones futuras en las entradas del Equipo 1, alternativamente maximizando el recurso utilizado por el Equipo 1 (es decir, wickets perdidos u overs lanzados) antes de que eso suceda. El Equipo 2 puede variar su estrategia de lanzamiento (entre conservadora y agresiva) para intentar lograr cualquiera de estos objetivos, por lo que esto significa hacer los mismos cálculos que se mencionaron anteriormente, ingresando sus opiniones sobre futuras carreras concedidas, wickets tomados y overs lanzados en cada estrategia de lanzamiento, para ver cuál es la mejor.
Además, el Equipo 2 puede alentar al Equipo 1 a batear de manera particularmente conservadora o agresiva (por ejemplo, a través de configuraciones de campo ).
Durante las entradas del equipo 2
Se establece un objetivo (de un número determinado de overs) para el Equipo 2 al comienzo de sus entradas. Si no habrá interrupciones futuras, entonces ambos equipos pueden jugar hasta el final de la manera normal. Sin embargo, si es probable que haya interrupciones en las entradas del Equipo 2, entonces el Equipo 2 intentará mantenerse por encima del puntaje par D/L, y el Equipo 1 intentará mantenerlo por detrás de él. Esto se debe a que, si un partido se abandona antes de que se complete el número determinado de overs, el Equipo 2 es declarado ganador si está por encima del puntaje par, y el Equipo 1 es declarado ganador si el Equipo 2 está por debajo del puntaje par. Se declara un empate si el Equipo 2 está exactamente en el puntaje par. (Esto se produce siempre que se haya lanzado un número mínimo de overs en las entradas del Equipo 2).
El par score aumenta con cada bola lanzada y cada wicket perdido, a medida que aumenta la cantidad de recursos utilizados. Como ejemplo, en la final de la Copa Mundial de Cricket de 2003, Australia bateó primero y anotó 359 en 50 overs. Cuando Australia completó sus 50 overs, sus recursos totales utilizaron R1=100%, por lo que el par score de India a lo largo de sus entradas fue: 359 x R2/100%, donde R2 es la cantidad de recursos utilizados hasta ese momento. Como se muestra en la primera línea de la tabla a continuación, después de 9 overs India estaba 57-1, y 41 overs y 9 wickets restantes equivalen al 85,3% de los recursos, por lo que se había utilizado 100% − 85,3% = 14,7%. El par score de India después de 9 overs fue, por lo tanto, 359 x 14,7%/100% = 52,773, que se redondea a la baja a 52.
Durante las seis bolas del décimo over, India anotó 0, 0, 0, 1 (de una bola nula), pérdida de wicket, 0. [50] Al comienzo del over, India estaba por delante del puntaje par, pero la pérdida del wicket hizo que su puntaje par saltara de 55 a 79, lo que los puso detrás del puntaje par.
| Sobreutilizados | 1 portillo perdido | 2 wickets perdidos | Puntuación real de la India | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Recursos restantes | Recursos utilizados (R2) | Puntuación par D/L | Recursos restantes | Recursos utilizados (R2) | Puntuación par D/L | ||||||
| 9.0 | 85,3% | 14,7% | 52.773 | 52 | 78,7% | 21,3% | 76.467 | 76 | 57-1 | ||
| 9.1 | 85,1% | 14,9% | 53.491 | 53 | 78,5% | 21,5% | 77.185 | 77 | 57-1 | ||
| 9.2 | 84,9% | 15,1% | 54.209 | 54 | 78,4% | 21,6% | 77.544 | 77 | 57-1 | ||
| 9.3 | 84,7% | 15,3% | 54.927 | 54 | 78,2% | 21,8% | 78.262 | 78 | 57-1 | ||
| 9.4 | 84,6% | 15,4% | 55.286 | 55 | 78,1% | 21,9% | 78.621 | 78 | 58-1 | ||
| 9.5 | 84,4% | 15,6% | 56.004 | 56 | 77,9% | 22,1% | 79.339 | 79 | 58-2 | ||
| 10.0 | 84,2% | 15,8% | 56.722 | 56 | 77,8% | 22,2% | 79.698 | 79 | 58-2 | ||
Otros usos
El método D/L tiene otros usos además de encontrar el puntaje final oficial actual para el equipo que batea segundo en un partido que ya se ha reducido por el clima.
Puntuación par bola por bola

.JPG/440px-2015_CWC_I_v_UAE_02-28_Scoreboard_(02).JPG)
Durante las entradas del segundo equipo, la cantidad de carreras que un equipo perseguidor esperaría haber anotado en promedio con esta cantidad de overs utilizados y wickets perdidos, si quisieran igualar con éxito el puntaje del primer equipo, llamado puntaje par D/L, puede mostrarse en una impresión de computadora, el marcador y/o la TV junto con el puntaje real, y actualizarse después de cada bola. Esto puede suceder en partidos que parece que están a punto de acortarse por el clima, y por lo tanto D/L está a punto de entrar en juego, o incluso en partidos que no se ven afectados por el clima en absoluto. Esto es:
- Para ayudar a los espectadores y jugadores a comprender si el equipo perseguidor está teniendo un mejor o peor desempeño de lo que necesitaría en promedio para alcanzar el puntaje objetivo.
- El puntaje del equipo que batea se compararía para determinar qué equipo había ganado, si el partido tuviera que abandonarse en ese momento. Es el puntaje par el que se muestra, es decir, el puntaje para empatar. El puntaje objetivo para ganar es una carrera más que esto. Sudáfrica salió de la Copa del Mundo de 2003 después de un empate con Sri Lanka al creer erróneamente que el puntaje par en la impresión era el puntaje objetivo [51] [52]
Cálculo de la tasa neta de ejecución
Se ha sugerido que cuando un equipo que batea en segundo lugar completa con éxito la persecución de carreras, se podría utilizar el método D/L para predecir cuántas carreras habrían anotado con una entrada completa (es decir, 50 overs en un One Day International) y utilizar esta predicción en el cálculo de la tasa neta de carreras . [53]
Esta sugerencia es en respuesta a las críticas a NRR de que no tiene en cuenta los wickets perdidos y que penaliza injustamente a los equipos que batean segundo y ganan, ya que esas entradas son más cortas y, por lo tanto, tienen menos peso en el cálculo de NRR que otras entradas que llegan hasta el final.
Crítica
El método D/L ha sido criticado con el argumento de que los wickets son un recurso con un peso mucho mayor que los overs, lo que lleva a la sugerencia de que si los equipos persiguen objetivos grandes y existe la posibilidad de lluvia, una estrategia ganadora podría ser no perder wickets y anotar a lo que parecería ser una tasa "perdedora" (por ejemplo, si la tasa requerida fuera 6,1, podría ser suficiente para anotar a 4,75 por over durante los primeros 20-25 overs). [54] La actualización de 2015 de DLS reconoció esta falla y cambió la tasa a la que los equipos debían anotar al comienzo de la segunda entrada en respuesta a una primera entrada grande.
Otra crítica es que el método D/L no tiene en cuenta los cambios en la proporción de entradas para las que existen restricciones de campo en comparación con un partido completo. [55]
Los esfuerzos más recientes han utilizado bases de datos ODI bola por bola de partidos realmente completados para evaluar la precisión del método. [56] Esos esfuerzos han concluido que el puntaje par DLS puede tener precisiones tan bajas como 50 a 60% para predecir el ganador final del partido cuando el equipo que batea segundo batea entre 20 y 24 overs y pierde entre 0 y 2 wickets.
Una crítica informal más común de los fanáticos del cricket y los periodistas sobre el método D/L es que es excesivamente complejo y puede malinterpretarse. [57] [58] Por ejemplo, en un partido de un día contra Inglaterra el 20 de marzo de 2009 , el entrenador de las Indias Occidentales ( John Dyson ) llamó a sus jugadores por mala iluminación, creyendo que su equipo ganaría por una carrera con el método D/L, pero sin darse cuenta de que la pérdida de un wicket con la última bola había alterado el puntaje de Duckworth-Lewis. De hecho, Javagal Srinath , el árbitro del partido, confirmó que las Indias Occidentales estaban a dos carreras de su objetivo, lo que le dio la victoria a Inglaterra.
También se han planteado inquietudes en cuanto a su idoneidad para los partidos Twenty20, donde un over con una puntuación alta puede alterar drásticamente la situación del juego, y la variabilidad de la tasa de carreras es mayor en partidos con un número menor de overs. [59]
Influencia cultural
El método Duckworth Lewis es el nombre de un grupo pop formado por Neil Hannon de The Divine Comedy y Thomas Walsh de Pugwash . Su primer lanzamiento fue un álbum homónimo, que incluye canciones con temática de cricket. [60] [61]
Notas
- ^ Esto supone que el partido se redujo a 45 overs por lado desde el principio, lo que refleja las condiciones en las que funcionaba el método de Overs Más Productivos en ese momento. Como la duración de ambas entradas se redujo debido a la lentitud de los lanzamientos de Sudáfrica, e Inglaterra perdió así los últimos overs más ingeniosos de sus entradas, el método Duckworth-Lewis también habría aumentado inicialmente el objetivo de Sudáfrica. [9] [10]
Referencias
- ^ "Una década de Duckworth-Lewis". BBC Sport . 1 de enero de 2007. Consultado el 21 de marzo de 2009 .
- ^ "Introducción al método Duckworth–Lewis–Stern". Cricbuzz. 12 de febrero de 2015. Consultado el 30 de marzo de 2015 .
- ^ S Rajesh (8 de junio de 2017). «Cómo funciona el método Duckworth–Lewis–Stern». Cricinfo . ESPN . Consultado el 13 de abril de 2018 .
- ^ Arvind, Rawat (14 de junio de 2024). "Método DLS en críquet: una guía de juego limpio en condiciones húmedas". stumpsinfo . Arvind . Consultado el 14 de junio de 2024 .
- ^ Andrew Miller (2007). "22 de una sola bola: una ridícula regla de lluvia deja a todos desconcertados". Cricinfo . ESPN Sports Media.
- ^ "Una década de Duckworth-Lewis". Cricinfo . ESPN Sports Media. 1 de enero de 2007.
- ^ "Una década de Duckworth-Lewis". BBC Sport . 1 de enero de 2007.
- ^ "Destruyan al prodigio barbudo". BBC Sport . 28 de marzo de 2007.
- ^ "Copa Mundial Benson & Hedges 1992 - Inglaterra vs Sudáfrica, 2da Semifinal en Sídney, 22 de marzo de 1992 - Cuadro de Mando Completo". ESPNcricinfo . Consultado el 24 de mayo de 2024 .
- ^ Monga, Sidharth (22 de marzo de 2020). "¿Realmente Sudáfrica tuvo mala suerte en el Mundial de 1992?". ESPNcricinfo . Consultado el 24 de mayo de 2024 .
- ^ "Cuadro de mando completo del segundo ODI de Zimbabue contra Inglaterra de 1997". Cricinfo . ESPN Sports Media. 1 de enero de 1997.
- ^ "El método Duckworth-Lewis". Data Analysis Australia. Septiembre de 2006. Archivado desde el original el 13 de julio de 2011. Consultado el 13 de junio de 2008 .
- ^ abcdefghijkl Frank Duckworth; Tony Lewis (diciembre de 2008). "Método D/L: respuestas a preguntas frecuentes". Cricinfo . ESPN Sports Media.
- ^ abc Duckworth, FC; Lewis, AJ (1998). "Un método justo para restablecer el objetivo en partidos de cricket de un día interrumpidos". Revista de la Sociedad de Investigación Operativa . 49 (3): 220–227. CiteSeerX 10.1.1.180.3272 . doi :10.1057/palgrave.jors.2600524. S2CID 2421934.
- ^ Duckworth, Frank (2008). "El método Duckworth/Lewis: un ejercicio de matemáticas, estadísticas, OR y comunicaciones" (PDF) . MSOR Connections . 8 (3). HE Academy: 11–14. doi :10.11120/msor.2008.08030011 (inactivo el 17 de mayo de 2024).
{{cite journal}}: CS1 maint: DOI inactivo a partir de mayo de 2024 ( enlace ) - ^ Duckworth, FC; Lewis, AJ (2004). "Una intervención de investigación operativa exitosa en el cricket de un día". Revista de la Sociedad de Investigación Operativa . 55 (7): 749–759. doi : 10.1057/palgrave.jors.2601717 . S2CID 28422411.
- ^ "Marcador completo del cuarto ODI de India vs Inglaterra 2008". Cricinfo . ESPN Sports Media. 23 de noviembre de 2008.
- ^ "Cuadro de mando completo Sudáfrica v India 5º ODI 2011". Cricinfo . ESPN Sports Media. 23 de enero de 2011.
- ^ "Cuadro de resultados completo del tercer ODI de Sri Lanka contra Inglaterra de 2014". Cricinfo . ESPN Sports Media. 3 de diciembre de 2014.
- ^ "2005-2006 Pakistán vs India - 1er ODI - Peshawar". HowStat! . 6 de febrero de 2006.
- ^ "Cuadro de resultados completo del partido Sri Lanka vs Zimbabwe del Grupo B del 7.º partido de la Copa Mundial T20 masculina de la ICC". Cricinfo . ESPN Sports Media. 3 de mayo de 2010.
- ^ Sriram Veera (3 de mayo de 2010). "Pisos de toneladas de Jayawardene en Zimbabwe". Cricinfo . Medios deportivos de ESPN.
- ^ "Cuadro de resultados completo de Perth Scorchers vs Melbourne Stars, segunda semifinal de la Big Bash League". Cricinfo . ESPN Sports Media. 16 de enero de 2013.
- ^ Alex Malcolm (16 de enero de 2013). "Los Scorchers se imponen en un partido dramático bajo la lluvia". Cricinfo . ESPN Sports Media.
- ^ Sharwood, Simon (12 de septiembre de 2016). "Simon Sharwood". The Register .(Entrevista al profesor Steven Sern)
- ^ abcdefg Método Duckworth/Lewis para recálculo del puntaje objetivo en un partido interrumpido ECB, 2013 Archivado el 22 de febrero de 2014 en Wayback Machine.
- ^ abc Frank Duckworth; Tony Lewis (2002). "El método Duckworth-Lewis (2002)". Cricinfo . ESPN Sports Media.
- ^ Frank Duckworth; Tony Lewis (1999). "El método Duckworth-Lewis (1999)". Cricinfo . ESPN Sports Media.
- ^ Frank Duckworth; Tony Lewis (2001). "El método Duckworth-Lewis (2001)". Cricinfo . ESPN Sports Media.
- ^ "Tony Lewis, de Duckworth-Lewis, entrevista: los periodistas denigran el sistema publicando 'basura' sin comprender". DNA . Diligent Media. 27 de agosto de 2013.
- ^ "ICC Playing Handbook 2013/14" (PDF) . Consejo Internacional de Críquet. 2013. pág. Sección 6 – vía Amazon Web Server.
- ^ abcdefghi «ICC Playing Handbook». Archivado desde el original el 19 de abril de 2014. Consultado el 18 de abril de 2014 .
- ^ Duckworth–Lewis revisará su fórmula para los partidos T20 Indian Express, 17 de junio de 2009 Archivado el 10 de octubre de 2012 en Wayback Machine
- ↑ Daniel Brettig (1 de marzo de 2015). «El método Duckworth-Lewis en un nuevo avatar para la Copa del Mundo». Cricinfo . ESPN Sports Media . Consultado el 7 de julio de 2016 .
- ^ Dr. Srinivas Bhogle (16 de septiembre de 1999). "La guía para principiantes de Duckworth-Lewis". Rediff en la red .
- ^ "ICC Playing Handbook 2006-07" (PDF) . Archivado desde el original (PDF) el 3 de marzo de 2016. Consultado el 18 de abril de 2014 .
- ^ "Cuadro de resultados completo de la liga Pro40 de Lancashire vs Hampshire". Cricinfo . ESPN Sports Media. 18 de mayo de 2003.
- ^ "Liga Nacional Lancashire v Hampshire 2003 (División 2)". Lancashire County Cricket Club. 18 de mayo de 2003 – vía CricketArchive.
- ^ Victor Isaacs (18 de mayo de 2003). "Un rayo azotó Hampshire entre las lluvias". Cricinfo . ESPN Sports Media.
- ^ "Cuadro de resultados completo de Sudáfrica vs Sri Lanka, Copa del Mundo, partido número 40". Cricinfo . ESPN Sports Media. 3 de marzo de 2003.
- ^ "Sudáfrica vs Sri Lanka". Wisden . ESPN Sports Media. 3 de marzo de 2003 – vía Cricinfo.
- ^ "Cuadro de resultados completo de Nueva Gales del Sur vs Australia del Sur, competencia doméstica australiana de un día". Cricinfo . ESPN Sports Media. 16 de febrero de 2003.
- ^ "Cuadro de puntuación". CricketArchive . (se requiere suscripción)
- ^ "Cuadro de resultados completo de West Indies vs Zimbabwe, Australia Tri Series (CB Series), 7.º partido". Cricinfo . ESPN Sports Media. 25 de enero de 2001.
- ^ "Cuadro de puntuación". CricketArchive . (se requiere suscripción)
- ^ "Cuadro de resultados completo de Australia vs Holanda, Copa del Mundo - Partido número 20". Cricinfo . ESPN Sports Media. 20 de febrero de 2003.
- ^ ab Keith Lane (20 de febrero de 2003). "El personal de campo de Potchefstroom ayuda a Australia a sumar cuatro puntos". Cricinfo . ESPN Sports Media.
- ^ "Australia vs Holanda". Wisden . ESPN Sports Media. 20 de febrero de 2003 – vía Cricinfo.
- ^ "Australia vs Holanda: más de una vez". BBC Sport . 20 de febrero de 2003.
- ^ "Final: Australia v India en Johannesburgo, comentarios pelota por pelota". Cricinfo . ESPN Sports Media. 23 de marzo de 2003.
- ^ Thrasy Petropoulos (3 de marzo de 2003). "Sudáfrica se deja lamer las heridas". BBC Sport .
- ^ Barney Ronay (17 de abril de 2011). "Ser Duckworth-Lewis: los matemáticos del cricket que rompen con el clima". The Guardian . Guardian News and Media.
- ^ Peter Foster (15 de abril de 2007). "Alternativa de tasa de ejecución neta". SportTaco.com .
- ^ Srinivas Bhogle (6 de marzo de 2003). "El factor Duckworth/Lewis". Rediff.com .
- ^ R Ramachandran Por una fórmula justa [usurpada] , The Hindu , 6 de diciembre de 2002
- ^ "¿Qué tan preciso es el método DLS? La opinión de un científico de datos". Medium. 11 de marzo de 2023.
- ^ Varma, Amit (25 de noviembre de 2004). "¿Simple y subjetivo? ¿O complejo y objetivo?". Cricinfo . ESPN Sports Media.
- ^ Brooker, Charlie (24 de abril de 2011). "Los activistas del AV han creado un remolino de estupidez que engulle cualquier molécula suelta de lógica". The Guardian . Consultado el 28 de abril de 2011 .
- ^ Rajeeva Karandikar; Srinivas Bhogle (13 de mayo de 2010). "La contracción anómala del método Duckworth-Lewis". Cricinfo . ESPN Sports Media.
- ^ "¿Qué tal un álbum de himnos?". Today . BBC Radio 4. 21 de mayo de 2009.
- ^ "¿Qué tal un nuevo álbum de cricket?". BBC News NI. 21 de mayo de 2009.
Lectura adicional
- Duckworth, FC y Lewis, AJ "Su guía completa sobre el método Duckworth Lewis para restablecer objetivos en el cricket de un día", Acumen Books, 2004 ISBN 0-9548718-0-4
- Duckworth, F "Un papel para las estadísticas en el críquet internacional" Teaching Statistics , (junio de 2001), volumen 23, n.º 2, págs. 38-44
- Duckworth, FC y Lewis, AJ "Un método justo para restablecer el objetivo en partidos de cricket de un día interrumpidos" Journal of the Operational Research Society , (marzo de 1998) Volumen 49, N.º 3, págs. 220-227 JSTOR 3010471
Enlaces externos
- El método D/L: respuestas a preguntas frecuentes (actualizado en septiembre de 2012) Consejo Internacional de Críquet, septiembre de 2012 (archivado el 6 de agosto de 2013)
- Método D/L de Frank Duckworth y Tony Lewis: respuestas a preguntas frecuentes ESPN Cricinfo, diciembre de 2008
- El método D/L (Duckworth/Lewis) para ajustar los puntajes objetivo en partidos de cricket de un día interrumpidos - Tabla de porcentajes de recursos del método D/L (edición estándar) del ICC Consejo Internacional de Cricket, 2002
- El método Duckworth-Lewis (2001) ESPN Cricinfo, 2001
- Objetivos afectados por la lluvia BBC Sport,
- Calculadora basada en la Web de Duckworth-Lewis.com para la edición estándar del método Duckworth Lewis
- Alternativas a D/L CricketArchive (se requiere suscripción)
- Documentos de Tony Lewis, estadístico, relacionados con el método de puntuación Duckworth-Lewis para partidos de críquet de un día. Centro de Registros Modernos, Universidad de Warwick, 1992-2009
- Una perspectiva de la ciencia de datos sobre la precisión del método DLS Desglose de la precisión del método DLS











