Sistema cristalino ortorrómbico
En cristalografía , el sistema cristalino ortorrómbico es uno de los 7 sistemas cristalinos . Las redes ortorrómbicas resultan de estirar una red cúbica a lo largo de dos de sus pares ortogonales por dos factores diferentes, lo que da como resultado un prisma rectangular con una base ( a por b ) y una altura ( c ) rectangulares, de modo que a , b y c son distintos. Las tres bases se intersecan en ángulos de 90°, por lo que los tres vectores de la red permanecen mutuamente ortogonales .
Celosías de Bravais
Hay cuatro redes de Bravais ortorrómbicas: ortorrómbica primitiva, ortorrómbica centrada en la base, ortorrómbica centrada en el cuerpo y ortorrómbica centrada en la cara.
| Celosía de Bravais | Ortorrómbico primitivo | Ortorrómbico centrado en la base | Ortorrómbico centrado en el cuerpo | Ortorrómbico centrado en la cara |
|---|---|---|---|---|
| Símbolo de Pearson | deo | sistema operativo | yo | de |
| Celda unitaria | 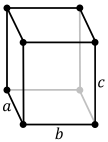 |  | 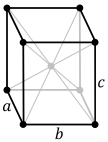 |  |
En el caso de la red ortorrómbica centrada en la base, la celda primitiva tiene la forma de un prisma rómbico recto; [1] se puede construir porque la capa base rectangular centrada bidimensional también se puede describir con ejes rómbicos primitivos. Nótese que la longitud de la celda primitiva de abajo es igual a la de la celda convencional de arriba.
Clases de cristales
Los nombres de las clases del sistema cristalino ortorrómbico , los ejemplos, la notación de Schönflies , la notación de Hermann-Mauguin , los grupos puntuales, el número de grupo espacial de las Tablas Internacionales de Cristalografía, [2] la notación orbifold , el tipo y los grupos espaciales se enumeran en la siguiente tabla.
| No. | Grupo de puntos | Tipo | Ejemplo | Grupos espaciales | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre [3] | Hermoso. | Internacional | Orbe. | Timonel. | Primitivo | Centrado en la base | Centrado en la cara | Centrado en el cuerpo | |||
| 16–24 | Difenoidal rómbico | D2 (V ) | 222 | 222 | [2,2] + | Enantiomórfico | Epsomita | P222, P222 1 , P2 1 2 1 2, P2 1 2 1 2 1 | C222 1 , C222 | F222 | yo222, yo2 1 2 1 2 1 |
| 25–46 | Pirámide rómbica | C2v | mm2 | *22 | [2] | Polar | Hemimorfita , bertrandita | Pmm2, Pmc2 1 , Pcc2, Pma2, Pca2 1 , Pnc2, Pmn2 1 , Pba2, Pna2 1 , Pnn2 | Cmm2, Cmc21 , Ccc2Amm2 , Aem2, Ama2, Aea2 | Fmm2, Fdd2 | Imm2, Iba2, Ima2 |
| 47–74 | Bipiramidal rómbico | D 2h ( Vh ) | mmm | *222 | [2,2] | Centrosimétrico | Olivino , aragonito , marcasita | Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma | Cmcm, Cmca, Cmmm, Cccm, Cmme, Ccce | Fmmm, Fddd | Immm, Ibam, Ibca, Imma |
En dos dimensiones
En dos dimensiones hay dos redes de Bravais ortorrómbicas: la rectangular primitiva y la rectangular centrada.
| Celosía de Bravais | Rectangular | Rectángulo centrado |
|---|---|---|
| Símbolo de Pearson | En | jefe |
| Celda unitaria | 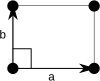 |  |
Véase también
Referencias
- ^ Véase Hahn (2002), pág. 746, fila oC, columna Primitiva, donde los parámetros de la celda se dan como a1 = a2, α = β = 90°
- ^ Prince, E., ed. (2006). Tablas internacionales de cristalografía . Unión Internacional de Cristalografía. doi :10.1107/97809553602060000001. ISBN 978-1-4020-4969-9.S2CID146060934 .
- ^ "Las 32 clases de cristales" . Consultado el 19 de junio de 2018 .
Lectura adicional
- Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual de mineralogía (20.ª edición). Págs. 69-73. ISBN 0-471-80580-7.
- Hahn, Theo, ed. (2002). Tablas internacionales de cristalografía, volumen A: Simetría de grupos espaciales. Tablas internacionales de cristalografía. Vol. A (5.ª ed.). Berlín, Nueva York: Springer-Verlag . doi :10.1107/97809553602060000100. ISBN . 978-0-7923-6590-7.

