Roseta Klemperer

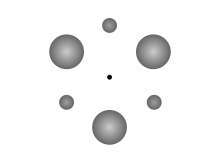
Una roseta de Klemperer es un sistema gravitacional de cuerpos más pesados ​​y más ligeros (opcionalmente) que se alternan y orbitan en un patrón simétrico alrededor de un baricentro común . Fue descrita por primera vez por WB Klemperer en 1962, ^[1] y es un caso especial de una configuración central .

Klemperer describió los sistemas de rosetas de la siguiente manera:

Esta simetría también la posee una peculiar familia de configuraciones geométricas que pueden describirse como "rosetas". En ellas, un número par de "planetas" de dos (o más) tipos, uno (o algunos) más pesado que el otro, pero todos de cada conjunto con la misma masa, se colocan en las esquinas de dos (o más) polígonos regulares entrelazados de modo que los más ligeros y los más pesados ​​se alternan (o se suceden uno tras otro de manera cíclica). ^{[1] (p. 163)}

La roseta más simple sería una serie de cuatro cuerpos más pesados ​​y más ligeros alternados, a 90 grados uno del otro, en una configuración rómbica [Pesado, Ligero, Pesado, Ligero], donde los dos cuerpos más grandes tienen la misma masa, y de la misma manera los dos cuerpos más pequeños tienen la misma masa, todos orbitando alrededor de su centro geométrico (vacío). El sistema troyano más general tiene masas desiguales para los dos cuerpos más pesados, que Klemperer también llama un sistema "rómbico", y es la única versión que no es simétrica alrededor del centro gravitacional.

Se puede aumentar el número de "tipos de masa", siempre que la disposición sea simétrica y tenga un patrón cíclico: p. ej., [ 1,2,3 ... 1,2,3 ], [ 1,2,3,4,5 ... 1,2,3,4,5 ], [ 1,2,3,3,2,1 ... 1,2,3,3,2,1 ], etc.

El artículo de Klemperer analiza específicamente polígonos regulares con 2-9 vértices ( desde los que tienen forma de mancuerna hasta los que tienen forma de nonágono ) y "rosetas rómbicas " no simétricas centralmente con tres cuerpos en órbita, los dos exteriores estacionados en los puntos triangulares del cuerpo en órbita central (L4 y L5), que ya habían sido descritos y estudiados por Lagrange en 1772. ^[2] Los sistemas con un número par de 4 o más vértices pueden tener masas pesadas y ligeras alternadas en los vértices, aunque el rango posible de proporciones de masas está limitado por requisitos de paraestabilidad; los sistemas con un número impar de vértices deben tener masas iguales en cada vértice. Si bien Klemperer señala que todas las rosetas y el rombo son vulnerables a la desestabilización, la roseta hexagonal es la más estable porque los "planetas" se encuentran en los puntos lagrangianos triangulares semiestables de cada uno , L4 y L5. ^{[1] (p. 165)}

Las configuraciones poligonales regulares ("rosetas") no requieren una masa central (un "sol" en el centro es opcional y, si está presente, puede oscilar por encima y por debajo del plano orbital), aunque un rombo de tipo Lagrange sí lo requiere. Si hay un cuerpo central, su masa restringe los rangos de la relación de masas entre los cuerpos en órbita. ^[1]

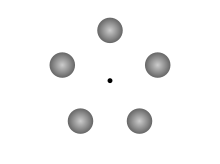
El término "roseta de Klemperer" (que a menudo se escribe mal " roseta de Kemplerer ") se utiliza para referirse a una configuración de tres o más masas iguales, dispuestas en los puntos de un polígono equilátero y a las que se les da una velocidad angular igual en torno a su centro de masas . Klemperer menciona esta configuración al comienzo de su artículo, pero sólo como un conjunto ya conocido de sistemas de equilibrio antes de introducir las rosetas reales.

En la novela de Larry Niven , Flota de Mundos , de la serie Ringworld , la epónima " Flota de Mundos " de los Titiriteros está dispuesta en una configuración ^[a] que Niven llama "roseta Kemplerer"; este error ortográfico (posiblemente intencional) es una fuente viable de la confusión más amplia. Es notable que estos planetas ficticios se mantuvieran en posición mediante grandes motores, además de la fuerza gravitacional.

Tanto el análisis de perturbación lineal simple como las simulaciones de rosetas ^[4] demuestran que tales sistemas son inestables: Klemperer explica en su artículo original que cualquier desplazamiento de la geometría perfectamente simétrica provoca una oscilación creciente, que eventualmente conduce a la interrupción del sistema. ^{[1] (pp 165-166)} El sistema es inestable independientemente de si el centro de la roseta está en el espacio libre o en órbita alrededor de una estrella central.

La explicación breve de la inestabilidad es que cualquier perturbación corrompe la simetría geométrica, lo que aumenta la perturbación y debilita aún más la geometría, y así sucesivamente. La explicación más larga es que cualquier perturbación tangencial acerca un cuerpo a un vecino y lo aleja de otro; el desequilibrio gravitacional se hace mayor hacia el vecino más cercano y menor para el vecino más lejano, atrayendo al objeto perturbado más hacia su vecino más cercano, amplificando la perturbación en lugar de amortiguarla. Una perturbación radial hacia adentro hace que el cuerpo perturbado se acerque a todos los demás objetos, lo que aumenta la fuerza sobre el objeto y aumenta su velocidad orbital, lo que conduce indirectamente a una perturbación tangencial y al argumento anterior. ^[b]

• Jenkins, Bob. "Rosetas de Klemperer". burtleburtle.net . Física . Consultado el 12 de enero de 2007 .— Simulaciones de rosetas

• "Rosette Kemplerer (Klemperer) de Larry Niven de Ringworld". technovelgy.com .