Árbol de búsqueda binaria
| Árbol de búsqueda binaria | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tipo | árbol | |||||||||||||||||||||||
| Inventado | 1960 | |||||||||||||||||||||||
| Inventado por | PF Windley, AD Booth , AJT Colin y TN Hibbard | |||||||||||||||||||||||
| ||||||||||||||||||||||||
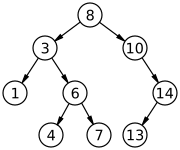
En informática , un árbol binario de búsqueda ( BST ), también llamado árbol binario ordenado , es una estructura de datos de árbol binario con raíz en la que la clave de cada nodo interno es mayor que todas las claves del subárbol izquierdo del nodo respectivo y menor que las de su subárbol derecho. La complejidad temporal de las operaciones en el árbol binario de búsqueda es lineal con respecto a la altura del árbol.
Los árboles de búsqueda binaria permiten realizar búsquedas binarias para buscar, agregar y eliminar elementos de datos rápidamente. Dado que los nodos de un árbol de búsqueda binaria están dispuestos de manera que cada comparación omite aproximadamente la mitad del árbol restante, el rendimiento de la búsqueda es proporcional al del logaritmo binario . Los árboles de búsqueda binaria se idearon en la década de 1960 para el problema del almacenamiento eficiente de datos etiquetados y se atribuyen a Conway Berners-Lee y David Wheeler .
El rendimiento de un árbol binario de búsqueda depende del orden de inserción de los nodos en el árbol, ya que las inserciones arbitrarias pueden provocar degeneración; se pueden crear varias variaciones del árbol binario de búsqueda con un rendimiento garantizado en el peor de los casos. Las operaciones básicas incluyen: búsqueda, recorrido, inserción y eliminación. Los BST con complejidades garantizadas en el peor de los casos funcionan mejor que una matriz no ordenada, que requeriría un tiempo de búsqueda lineal .
El análisis de complejidad de BST muestra que, en promedio , la inserción, eliminación y búsqueda toma nodos . En el peor de los casos, se degradan al nivel de una lista enlazada simple: . Para abordar el aumento ilimitado de la altura del árbol con inserciones y eliminaciones arbitrarias, se introducen variantes autoequilibradas de BST para limitar la peor complejidad de búsqueda a la del logaritmo binario. Los árboles AVL fueron los primeros árboles de búsqueda binarios autoequilibrados, inventados en 1962 por Georgy Adelson-Velsky y Evgenii Landis .
Los árboles de búsqueda binaria se pueden utilizar para implementar tipos de datos abstractos , como conjuntos dinámicos , tablas de búsqueda y colas de prioridad , y se pueden utilizar en algoritmos de ordenación como la ordenación de árboles .
Historia
El algoritmo de árbol binario de búsqueda fue descubierto independientemente por varios investigadores, entre ellos PF Windley, Andrew Donald Booth , Andrew Colin y Thomas N. Hibbard . [1] [2] El algoritmo se atribuye a Conway Berners-Lee y David Wheeler , quienes lo utilizaron para almacenar datos etiquetados en cintas magnéticas en 1960. [3] Uno de los primeros y más populares algoritmos de árbol binario de búsqueda es el de Hibbard. [1]
Las complejidades temporales de un árbol binario de búsqueda aumentan sin límites con la altura del árbol si los nodos se insertan en un orden arbitrario, por lo tanto, se introdujeron árboles binarios de búsqueda autoequilibrados para limitar la altura del árbol a . [4] Se introdujeron varios árboles binarios de búsqueda con equilibrio de altura para limitar la altura del árbol, como los árboles AVL , Treaps y los árboles rojo-negros . [5]
El árbol AVL fue inventado por Georgy Adelson-Velsky y Evgenii Landis en 1962 para la organización eficiente de la información. [6] [7] Fue el primer árbol binario de búsqueda autoequilibrado que se inventó. [8]
Descripción general
Un árbol binario de búsqueda es un árbol binario con raíz en el que los nodos están dispuestos en un orden total estricto en el que los nodos con claves mayores que cualquier nodo particular A se almacenan en los subárboles de la derecha de ese nodo A y los nodos con claves iguales o menores que A se almacenan en los subárboles de la izquierda de A, satisfaciendo la propiedad de búsqueda binaria . [9] : 298 [10] : 287
Los árboles binarios de búsqueda también son eficaces en ordenaciones y algoritmos de búsqueda . Sin embargo, la complejidad de búsqueda de un BST depende del orden en el que se insertan y eliminan los nodos; dado que en el peor de los casos, las operaciones sucesivas en el árbol binario de búsqueda pueden llevar a la degeneración y formar una estructura similar a una lista enlazada simple (o "árbol desequilibrado"), tiene por tanto la misma complejidad en el peor de los casos que una lista enlazada . [11] [9] : 299-302
Los árboles de búsqueda binaria también son una estructura de datos fundamental utilizada en la construcción de estructuras de datos abstractas como conjuntos, multiconjuntos y matrices asociativas .
Operaciones
Búsqueda
La búsqueda de una clave específica en un árbol de búsqueda binario se puede programar de forma recursiva o iterativa .
La búsqueda comienza examinando el nodo raíz . Si el árbol es nulo , la clave que se busca no existe en el árbol. De lo contrario, si la clave es igual a la de la raíz, la búsqueda es exitosa y se devuelve el nodo. Si la clave es menor que la de la raíz, la búsqueda continúa examinando el subárbol izquierdo. De manera similar, si la clave es mayor que la de la raíz, la búsqueda continúa examinando el subárbol derecho. Este proceso se repite hasta que se encuentra la clave o el subárbol restante es nulo . Si la clave buscada no se encuentra después de alcanzar un subárbol, entonces la clave no está presente en el árbol. [10] : 290–291
Búsqueda recursiva
El siguiente pseudocódigo implementa el procedimiento de búsqueda BST a través de recursión . [10] : 290
Búsqueda-de-árbol-recursivo(x, clave) si x = NIL o clave = x.clave entonces devuelve x si clave < x.clave entonces devuelve Búsqueda-de-árbol-recursivo(x.izquierda, clave) de lo contrario devuelve Búsqueda-de-árbol-recursivo(x.derecha, clave) fin si |
El procedimiento recursivo continúa hasta que se encuentra a o lo que se busca.
Búsqueda iterativa
La versión recursiva de la búsqueda se puede "desenrollar" en un bucle while . En la mayoría de las máquinas, se ha comprobado que la versión iterativa es más eficiente . [10] : 291
Búsqueda de árbol iterativo (x, clave) mientras x ≠ NIL y clave ≠ x.clave haga si clave < x.clave entonces x := x.izquierda demás x := x.derecha Fin si se repite el retorno x |
Dado que la búsqueda puede continuar hasta algún nodo de hoja , la complejidad del tiempo de ejecución de la búsqueda BST es donde es la altura del árbol . Sin embargo, el peor caso para la búsqueda BST es donde es el número total de nodos en la BST, porque una BST desequilibrada puede degenerar en una lista enlazada. Sin embargo, si la BST está equilibrada en altura, la altura es . [10] : 290
Sucesor y predecesor
Para ciertas operaciones, dado un nodo , encontrar el sucesor o predecesor de es crucial. Suponiendo que todas las claves de una BST son distintas, el sucesor de un nodo en una BST es el nodo con la clave más pequeña que la clave de . Por otro lado, el predecesor de un nodo en una BST es el nodo con la clave más grande que sea menor que la clave de . El siguiente pseudocódigo encuentra el sucesor y predecesor de un nodo en una BST. [12] [13] [10] : 292–293
BST-Successor(x) si x.right ≠ NIL entonces devuelve BST-Minimum(x.right) fin si y := x.padre mientras y ≠ NIL y x = y.derecha x := y y := y.padre repetir retorno y | BST-Predecesor(x) si x.left ≠ NIL entonces devuelve BST-Máximo(x.left) fin si y := x.padre mientras y ≠ NIL y x = y.left hacer x := y y := y.padre repetir retorno y |
Operaciones como la búsqueda de un nodo en una BST cuya clave sea el máximo o el mínimo son críticas en ciertas operaciones, como la determinación del sucesor y predecesor de los nodos. A continuación se muestra el pseudocódigo para las operaciones. [10] : 291–292
BST-Máximo(x) mientras x.derecha ≠ NIL hacer x := x.derecha repetir retorno x | BST-Mínimo(x) mientras x.izquierda ≠ NIL hacer x := x.izquierda repetir retorno x |
Inserción
Las operaciones como la inserción y la eliminación hacen que la representación de la BST cambie dinámicamente. La estructura de datos debe modificarse de manera que las propiedades de la BST sigan siendo válidas. Los nuevos nodos se insertan como nodos hoja en la BST. [10] : 294–295 A continuación se muestra una implementación iterativa de la operación de inserción. [10] : 294
1 BST-Insertar(T, z)2 y := NULO3 x := T.raíz4 mientras x ≠ NIL hacer5 y := x6 si tecla z < tecla x entonces7 x := x.izquierda8 más9 x := x.derecha10 termina si 11 repite12 z.padre := y13 si y = NIL entonces14 T.raíz := z15 de lo contrario si z.key < y.key entonces16 y.izquierda := z17 más18 y.derecha := z19 fin si |
El procedimiento mantiene un "puntero final" como padre de . Después de la inicialización en la línea 2, el bucle while a lo largo de las líneas 4-11 hace que se actualicen los punteros. Si es , el BST está vacío, por lo que se inserta como el nodo raíz del árbol binario de búsqueda ; si no es , la inserción continúa comparando las claves con las de en las líneas 15-19 y el nodo se inserta en consecuencia. [10] : 295
Supresión

La eliminación de un nodo, por ejemplo , del árbol binario de búsqueda tiene tres casos: [10] : 295-297
- Si es un nodo hoja, el nodo padre de se reemplaza por y, en consecuencia, se elimina de , como se muestra en (a).
- Si solo tiene un hijo, el nodo hijo de se eleva modificando el nodo padre de para que apunte al nodo hijo, tomando en consecuencia la posición de en el árbol, como se muestra en (b) y (c).
- Si tiene hijos tanto izquierdos como derechos, el sucesor de , digamos , desplaza siguiendo los dos casos:
- Si es el hijo derecho de , como se muestra en (d), desplaza y el hijo derecho de permanece sin cambios.
- Si se encuentra dentro del subárbol derecho de pero no es el hijo derecho de , como se muestra en (e), primero se reemplaza por su propio hijo derecho y luego desplaza la posición de en el árbol.
El siguiente pseudocódigo implementa la operación de eliminación en un árbol de búsqueda binario. [10] : 296-298
1 BST-Eliminar(BST, D)2 si D.izquierda = NIL entonces3 nodos de desplazamiento (BST, D, D.derecha)4 de lo contrario si D.right = NIL entonces5 nodos de cambio (BST, D, D.izquierda)6 más7 E := BST-Sucesor(D)8 si E.parent ≠ D entonces9 nodos de desplazamiento (BST, E, E.derecha)10 E.derecha := D.derecha11 E.derecho.padre := E12 fin si13 nodos de cambio (BST, D, E)14 E.izquierda := D.izquierda15 E.izquierda.padre := E16 fin si |
1 Nodos de desplazamiento (BST, u, v)2 si u.parent = NIL entonces3 BST.raíz := v4 de lo contrario si u = u.parent.left entonces5 u.padre.izquierda := v5 más6 u.padre.derecho := v7 fin si 8 si v ≠ NIL entonces9 v.padre := u.padre10 fin si |
El procedimiento se ocupa de los 3 casos especiales mencionados anteriormente. Las líneas 2-3 se ocupan del caso 1; las líneas 4-5 se ocupan del caso 2 y las líneas 6-16 del caso 3. La función auxiliar se utiliza dentro del algoritmo de eliminación con el fin de reemplazar el nodo con en el árbol de búsqueda binaria . [10] : 298 Este procedimiento maneja la eliminación (y sustitución) de from .
Travesía
Se puede recorrer un BST a través de tres algoritmos básicos: recorridos de árbol en orden , preorden y postorden . [10] : 287
- Recorrido por el árbol en orden : primero se visitan los nodos del subárbol izquierdo, seguidos del nodo raíz y del subárbol derecho. Este recorrido visita todos los nodos en el orden de la secuencia de teclas no decreciente.
- Recorrido por el árbol en preorden : primero se visita el nodo raíz, seguido de los subárboles izquierdo y derecho.
- Recorrido por árbol postorden : primero se visitan los nodos del subárbol izquierdo, seguidos por el subárbol derecho y, finalmente, la raíz.
A continuación se muestra una implementación recursiva de los recorridos por el árbol. [10] : 287–289
Inorder-Tree-Walk(x) si x ≠ NIL entonces Paseo por el árbol en orden (x.izquierda) Visita el nodo Paseo por el árbol en orden (x.derecha) terminar si | Preorder-Tree-Walk(x) si x ≠ NIL entonces visita el nodo Pedido anticipado: Paseo por el árbol (x.izquierda) Pedido anticipado Paseo por el árbol (x.derecha) terminar si | Postorder-Tree-Walk(x) si x ≠ NIL entonces Paseo por el árbol en orden posterior (x.izquierda) Paseo por el árbol en orden posterior (x.derecha) Visita el nodo final si |
Árboles de búsqueda binarios balanceados
Sin un reequilibrio, las inserciones o eliminaciones en un árbol binario de búsqueda pueden provocar una degeneración, lo que da como resultado una altura del árbol (donde es el número de elementos en un árbol), de modo que el rendimiento de la búsqueda se deteriora al de una búsqueda lineal. [14] Mantener el árbol de búsqueda equilibrado y la altura limitada por es una clave para la utilidad del árbol binario de búsqueda. Esto se puede lograr mediante mecanismos de "autoequilibrio" durante las operaciones de actualización del árbol diseñados para mantener la altura del árbol a la complejidad logarítmica binaria. [4] [15] : 50
Árboles de altura equilibrada
Un árbol está equilibrado en altura si se garantiza que las alturas del subárbol izquierdo y del subárbol derecho están relacionadas por un factor constante. Esta propiedad fue introducida por el árbol AVL y continuada por el árbol rojo-negro . [15] : 50–51 Las alturas de todos los nodos en la ruta desde la raíz hasta el nodo de hoja modificado deben observarse y posiblemente corregirse en cada operación de inserción y eliminación del árbol. [15] : 52
Árboles con peso equilibrado
En un árbol equilibrado por peso, el criterio de un árbol equilibrado es el número de hojas de los subárboles. Los pesos de los subárboles izquierdo y derecho difieren como máximo en . [16] [15] : 61 Sin embargo, la diferencia está limitada por una relación de los pesos, ya que no se puede mantener una condición de equilibrio fuerte de con el trabajo de reequilibrio durante las operaciones de inserción y eliminación. Los árboles equilibrados por peso dan una familia completa de condiciones de equilibrio, donde cada subárbol izquierdo y derecho tienen cada uno al menos una fracción de del peso total del subárbol. [15] : 62
Tipos
Hay varios árboles de búsqueda binarios autoequilibrados, incluidos el árbol T , [17] treap , [18] el árbol rojo-negro , [19] el árbol B , [20] el árbol 2-3 , [21] y el árbol Splay . [22]
Ejemplos de aplicaciones
Clasificar
Los árboles de búsqueda binaria se utilizan en algoritmos de ordenamiento como el de ordenamiento de árboles , donde todos los elementos se insertan a la vez y el árbol se recorre en orden. [23] Los BST también se utilizan en el ordenamiento rápido . [24]
Operaciones de cola de prioridad
Los árboles de búsqueda binaria se utilizan para implementar colas de prioridad , utilizando la clave del nodo como prioridad. La adición de nuevos elementos a la cola sigue la operación de inserción BST habitual, pero la operación de eliminación depende del tipo de cola de prioridad: [25]
- Si se trata de una cola de prioridad de orden ascendente, la eliminación de un elemento con la prioridad más baja se realiza mediante un recorrido hacia la izquierda de la BST.
- Si se trata de una cola de prioridad de orden descendente, la eliminación de un elemento con la prioridad más alta se realiza mediante un recorrido hacia la derecha de la BST.
Véase también
Referencias
- ^ ab Culberson, J.; Munro, JI (1 de enero de 1989). "Explicación del comportamiento de los árboles binarios de búsqueda bajo actualizaciones prolongadas: un modelo y simulaciones". The Computer Journal . 32 (1): 68–69. doi : 10.1093/comjnl/32.1.68 .
- ^ Culberson, J.; Munro, JI (28 de julio de 1986). "Análisis de los algoritmos de eliminación estándar en árboles de búsqueda binaria de dominio de ajuste exacto". Algorithmica . 5 (1–4). Springer Publishing , Universidad de Waterloo : 297. doi :10.1007/BF01840390. S2CID 971813.
- ^ PF Windley (1 de enero de 1960). "Árboles, bosques y reorganización". The Computer Journal . 3 (2): 84. doi : 10.1093/comjnl/3.2.84 .
- ^ ab Knuth, Donald (1998). "Sección 6.2.3: Árboles equilibrados". El arte de la programación informática (PDF) . Vol. 3 (2.ª ed.). Addison-Wesley . págs. 458–481. ISBN. 978-0201896855. Archivado (PDF) del original el 9 de octubre de 2022.
- ^ Paul E. Black, "árbol rojo-negro", en Dictionary of Algorithms and Data Structures [en línea], Paul E. Black, ed. 12 de noviembre de 2019. (consultado el 19 de mayo de 2022) de: https://www.nist.gov/dads/HTML/redblack.html
- ^ Myers, Andrew. "CS 312 Lecture: AVL Trees". Universidad de Cornell , Departamento de Ciencias de la Computación. Archivado desde el original el 27 de abril de 2021. Consultado el 19 de mayo de 2022 .
- ^ Adelson-Velsky, Georgy; Landis, Evgenii (1962). "Un algoritmo para la organización de la información". Actas de la Academia de Ciencias de la URSS (en ruso). 146 : 263–266.Traducción al inglés de Myron J. Ricci en Soviet Mathematics - Doklady , 3:1259–1263, 1962.
- ^ Pitassi, Toniann (2015). «CSC263: Balanced BSTs, AVL tree» (PDF) . Universidad de Toronto , Departamento de Ciencias de la Computación. pág. 6. Archivado (PDF) del original el 14 de febrero de 2019. Consultado el 19 de mayo de 2022 .
- ^ ab Thareja, Reema (13 de octubre de 2018). "Hashing y colisión". Estructuras de datos con C (2.ª edición). Oxford University Press . ISBN 9780198099307.
- ^ abcdefghijklmno Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2001). Introducción a los algoritmos (2ª ed.). Prensa del MIT . ISBN 0-262-03293-7.
- ^ RA Frost; MM Peterson (1 de febrero de 1982). "Una breve nota sobre árboles binarios de búsqueda". The Computer Journal . 25 (1). Oxford University Press : 158. doi :10.1093/comjnl/25.1.158.
- ^ Junzhou Huang. «Diseño y análisis de algoritmos» (PDF) . Universidad de Texas en Arlington . pág. 12. Archivado (PDF) del original el 13 de abril de 2021. Consultado el 17 de mayo de 2021 .
- ^ Ray, Ray. "Binary Search Tree". Universidad Loyola Marymount , Departamento de Ciencias de la Computación . Consultado el 17 de mayo de 2022 .
- ^ Thornton, Alex (2021). «ICS 46: Binary Search Trees». Universidad de California, Irvine . Archivado desde el original el 4 de julio de 2021. Consultado el 21 de octubre de 2021 .
- ^ abcde Brass, Peter (enero de 2011). Estructura de datos avanzada. Cambridge University Press . doi :10.1017/CBO9780511800191. ISBN 9780511800191.
- ^ Blum, Norbert; Mehlhorn, Kurt (1978). "Sobre el número medio de operaciones de reequilibrio en árboles con equilibrio de peso" (PDF) . Theoretical Computer Science . 11 (3): 303–320. doi :10.1016/0304-3975(80)90018-3. Archivado (PDF) desde el original el 2022-10-09.
- ^ Lehman, Tobin J.; Carey, Michael J. (25–28 de agosto de 1986). Un estudio de estructuras de índice para sistemas de gestión de bases de datos en memoria principal . Duodécima Conferencia Internacional sobre Bases de Datos de Gran Tamaño (VLDB 1986). Kioto. ISBN 0-934613-18-4.
- ^ Aragon, Cecilia R.; Seidel, Raimund (1989), "Randomized Search Trees" (PDF) , 30.º Simposio anual sobre fundamentos de la informática , Washington, DC: IEEE Computer Society Press, págs. 540-545, doi :10.1109/SFCS.1989.63531, ISBN 0-8186-1982-1, archivado (PDF) del original el 2022-10-09
- ^ Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001). "Árboles rojos y negros". Introducción a los algoritmos (segunda edición). MIT Press. págs. 273–301. ISBN 978-0-262-03293-3.
- ^ Comer, Douglas (junio de 1979), "El árbol B ubicuo", Computing Surveys , 11 (2): 123–137, doi : 10.1145/356770.356776 , ISSN 0360-0300, S2CID 101673
- ^ Knuth, Donald M (1998). "6.2.4". El arte de la programación informática . Vol. 3 (2.ª ed.). Addison Wesley. ISBN 9780201896855Los árboles
2-3 definidos al final de la Sección 6.2.3 son equivalentes a árboles B de orden 3.
- ^ Sleator, Daniel D. ; Tarjan, Robert E. (1985). "Árboles de búsqueda binaria autoajustables" (PDF) . Revista de la ACM . 32 (3): 652–686. doi :10.1145/3828.3835. S2CID 1165848.
- ^ Narayanan, Arvind (2019). «COS226: Binary search trees» (Árboles de búsqueda binaria COS226). Facultad de Ingeniería y Ciencias Aplicadas de la Universidad de Princeton . Archivado desde el original el 22 de marzo de 2021. Consultado el 21 de octubre de 2021 en cs.princeton.edu.
- ^ Xiong, Li. "Una conexión entre árboles de búsqueda binaria y ordenación rápida". Oxford College of Emory University , Departamento de Matemáticas y Ciencias de la Computación. Archivado desde el original el 26 de febrero de 2021. Consultado el 4 de junio de 2022 .
- ^ Myers, Andrew. "CS 2112 Lecture and Recite Notes: Priority Queues and Heaps". Universidad de Cornell , Departamento de Ciencias de la Computación . Archivado desde el original el 21 de octubre de 2021. Consultado el 21 de octubre de 2021 .
Lectura adicional
 Este artículo incorpora material de dominio público de Paul E. Black. "Binary Search Tree". Diccionario de algoritmos y estructuras de datos . NIST .
Este artículo incorpora material de dominio público de Paul E. Black. "Binary Search Tree". Diccionario de algoritmos y estructuras de datos . NIST .- Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2001). "12: Árboles binarios de búsqueda, 15.5: Árboles binarios de búsqueda óptimos". Introducción a los algoritmos (2.ª ed.). MIT Press . págs. 253–272, 356–363. ISBN 0-262-03293-7.
- Jarc, Duane J. (3 de diciembre de 2005). "Binary Tree Traversals". Visualizaciones interactivas de estructuras de datos . Universidad de Maryland . Archivado desde el original el 27 de febrero de 2014. Consultado el 30 de abril de 2006 .
- Knuth, Donald (1997). "6.2.2: Búsqueda en árboles binarios". El arte de la programación informática . Vol. 3: "Ordenación y búsqueda" (3.ª ed.). Addison-Wesley. págs. 426–458. ISBN 0-201-89685-0.
- Long, Sean. "Árbol de búsqueda binaria" ( PPT ) . Visualización de estructuras de datos y algoritmos: un enfoque basado en diapositivas de PowerPoint . SUNY Oneonta .
- Parlante, Nick (2001). "Binary Trees". Biblioteca de Educación en Ciencias de la Computación . Universidad de Stanford . Archivado desde el original el 30 de enero de 2022.
Enlaces externos
- Ben Pfaff: Introducción a los árboles binarios de búsqueda y árboles equilibrados. (PDF; 1675 kB) 2004.
- Visualizador de árboles binarios (animación en JavaScript de varias estructuras de datos basadas en BT)






















