Árbol R de Hilbert

El árbol R de Hilbert , una variante del árbol R , es un índice para objetos multidimensionales como líneas, regiones, objetos 3D u objetos paramétricos basados ​​en características de alta dimensión. Se puede considerar como una extensión del árbol B+ para objetos multidimensionales.

El rendimiento de los árboles R depende de la calidad del algoritmo que agrupa los rectángulos de datos en un nodo. Los árboles R de Hilbert utilizan curvas de relleno de espacio , y específicamente la curva de Hilbert , para imponer un ordenamiento lineal en los rectángulos de datos.

Existen dos tipos de árboles R de Hilbert: uno para bases de datos estáticas y otro para bases de datos dinámicas . En ambos casos se utilizan curvas de relleno de espacio de Hilbert para lograr un mejor ordenamiento de los objetos multidimensionales en el nodo. Este ordenamiento tiene que ser "bueno", en el sentido de que debe agrupar rectángulos de datos "similares" para minimizar el área y el perímetro de los rectángulos delimitadores mínimos (MBR) resultantes. Los árboles R de Hilbert empaquetados son adecuados para bases de datos estáticas en las que las actualizaciones son muy poco frecuentes o en las que no hay actualizaciones en absoluto.

El árbol R de Hilbert dinámico es adecuado para bases de datos dinámicas donde las inserciones, eliminaciones o actualizaciones pueden ocurrir en tiempo real. Además, los árboles R de Hilbert dinámicos emplean un mecanismo flexible de división diferida para aumentar la utilización del espacio. Cada nodo tiene un conjunto bien definido de nodos hermanos. Esto se hace proponiendo un ordenamiento en los nodos del árbol R. El árbol R de Hilbert ordena los rectángulos según el valor de Hilbert del centro de los rectángulos (es decir, MBR). (El valor de Hilbert de un punto es la longitud de la curva de Hilbert desde el origen hasta el punto). Dado el ordenamiento, cada nodo tiene un conjunto bien definido de nodos hermanos; por lo tanto, se puede utilizar la división diferida. Al ajustar la política de división, el árbol R de Hilbert puede lograr un grado de utilización del espacio tan alto como se desee. Por el contrario, otras variantes del árbol R no tienen control sobre la utilización del espacio.

Aunque el siguiente ejemplo corresponde a un entorno estático, explica los principios intuitivos para un buen diseño de árbol R. Estos principios son válidos tanto para bases de datos estáticas como dinámicas.

Roussopoulos y Leifker propusieron un método para construir un árbol R empaquetado que logra una utilización del espacio de casi el 100%. La idea es ordenar los datos en la coordenada x o y de una de las esquinas de los rectángulos. La ordenación en cualquiera de las cuatro coordenadas da resultados similares. En este análisis, los puntos o rectángulos se ordenan en la coordenada x de la esquina inferior izquierda del rectángulo, lo que se conoce como un "árbol R empaquetado lowx". La lista ordenada de rectángulos se escanea; los rectángulos sucesivos se asignan al mismo nodo hoja del árbol R hasta que ese nodo esté lleno; luego se crea un nuevo nodo hoja y se continúa el escaneo de la lista ordenada. De este modo, los nodos del árbol R resultante estarán completamente empaquetados, con la posible excepción del último nodo en cada nivel. Esto lleva a una utilización del espacio de aproximadamente el 100%. Los niveles superiores del árbol se crean de manera similar.

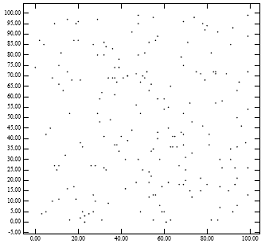
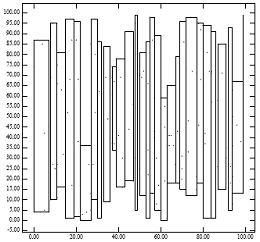
La Figura 1 destaca el problema del árbol R empaquetado con lowx. La Figura 1 [derecha] muestra los nodos de hoja del árbol R que el método de empaquetado con lowx creará para los puntos de la Figura 1 [izquierda]. El hecho de que los nodos padre resultantes cubran un área pequeña explica por qué el árbol R empaquetado con lowx logra un rendimiento excelente para consultas de puntos. Sin embargo, el hecho de que los padres tengan perímetros grandes explica la degradación del rendimiento para consultas de región. Esto es consistente con las fórmulas analíticas para el rendimiento del árbol R. ^[1] Intuitivamente, el algoritmo de empaquetado idealmente debería asignar puntos cercanos al mismo nodo de hoja. La ignorancia de la coordenada y por parte del árbol R empaquetado con lowx tiende a violar esta regla empírica.

Figura 1: [Izquierda] 200 puntos distribuidos uniformemente; [Derecha] MBR de nodos generados por el algoritmo "lowx packed R-tree"

La sección siguiente describe dos variantes de los árboles R de Hilbert. El primer índice es adecuado para bases de datos estáticas en las que las actualizaciones son muy poco frecuentes o en las que no hay actualizaciones en absoluto. Los nodos del árbol R resultante estarán completamente empaquetados, con la posible excepción del último nodo de cada nivel. Por lo tanto, la utilización del espacio es de aproximadamente el 100 %; esta estructura se denomina árbol R de Hilbert empaquetado. El segundo índice, denominado árbol R de Hilbert dinámico, admite inserciones y eliminaciones y es adecuado para un entorno dinámico.

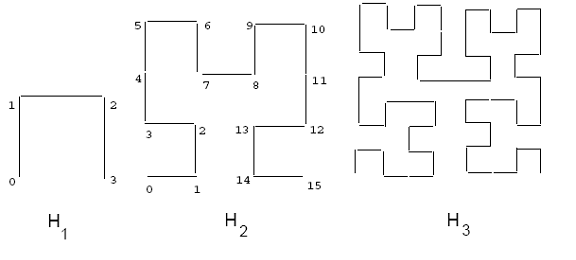
A continuación se ofrece una breve introducción a la curva de Hilbert . La curva de Hilbert básica en una cuadrícula de 2x2, denotada por H _1, se muestra en la Figura 2. Para derivar una curva de orden i, cada vértice de la curva básica se reemplaza por la curva de orden i – 1, que puede rotarse y/o reflejarse apropiadamente. La Figura 2 también muestra las curvas de Hilbert de orden dos y tres. Cuando el orden de la curva tiende al infinito, como otras curvas que llenan el espacio, la curva resultante es un fractal, con una dimensión fractal de dos. ^{[1] [2]} La curva de Hilbert se puede generalizar para dimensionalidades superiores. Los algoritmos para dibujar la curva bidimensional de un orden dado se pueden encontrar en ^[3] y. ^[2] Se proporciona un algoritmo para dimensionalidades superiores en. ^[4]

La trayectoria de una curva que llena el espacio impone un ordenamiento lineal en los puntos de la cuadrícula; esta trayectoria se puede calcular comenzando en un extremo de la curva y siguiendo la trayectoria hasta el otro extremo. Se pueden calcular los valores de coordenadas reales de cada punto. Sin embargo, para la curva de Hilbert esto es mucho más difícil que, por ejemplo, para la curva de orden Z. La Figura 2 muestra un ordenamiento de este tipo para una cuadrícula de 4x4 (ver curva H ₂ ). Por ejemplo, el punto (0,0) en la curva H ₂ tiene un valor de Hilbert de 0, mientras que el punto (1,1) tiene un valor de Hilbert de 2. El valor de Hilbert de un rectángulo se define como el valor de Hilbert de su centro.

Figura 2: Curvas de Hilbert de orden 1, 2 y 3

La curva de Hilbert impone un ordenamiento lineal sobre los rectángulos de datos y luego recorre la lista ordenada, asignando cada conjunto de rectángulos C a un nodo en el árbol R. El resultado final es que el conjunto de rectángulos de datos en el mismo nodo estará cerca uno del otro en el ordenamiento lineal, y muy probablemente en el espacio nativo; por lo tanto, los nodos del árbol R resultantes tendrán áreas más pequeñas. La Figura 2 ilustra las razones intuitivas por las que nuestros métodos basados ​​en Hilbert darán como resultado un buen rendimiento. Los datos están compuestos de puntos (los mismos puntos que se dan en la Figura 1). Al agrupar los puntos según sus valores de Hilbert, los MBR de los nodos del árbol R resultantes tienden a ser pequeños rectángulos de tipo cuadrado. Esto indica que los nodos probablemente tendrán un área pequeña y perímetros pequeños. Los valores de área pequeños dan como resultado un buen rendimiento para consultas de puntos; los valores de área pequeña y perímetro pequeño dan como resultado un buen rendimiento para consultas más grandes.

(empaqueta rectángulos en un árbol R)
Paso 1. Calcular el valor de Hilbert para cada rectángulo de datos
Paso 2. Ordenar los rectángulos de datos según valores de Hilbert ascendentes
Paso 3. /* Crear nodos de hoja (nivel l=0) */

• Mientras (hay más rectángulos)
  • generar un nuevo nodo de árbol R
  • Asignar los siguientes rectángulos C a este nodo

Paso 4. /* Crear nodos en un nivel superior (l + 1) */

• Mientras (hay > 1 nodos en el nivel l)
  • ordenar nodos en el nivel l ≥ 0 en tiempo de creación ascendente
  • repita el paso 3

En este caso, se supone que los datos son estáticos o que la frecuencia de modificación es baja. Se trata de una heurística sencilla para construir un árbol R con una utilización del espacio de aproximadamente el 100 % que, al mismo tiempo, tendrá un buen tiempo de respuesta.

El rendimiento de los árboles R depende de la calidad del algoritmo que agrupa los rectángulos de datos en un nodo. Los árboles R de Hilbert utilizan curvas que rellenan el espacio, y específicamente la curva de Hilbert, para imponer un ordenamiento lineal en los rectángulos de datos. El valor de Hilbert de un rectángulo se define como el valor de Hilbert de su centro.

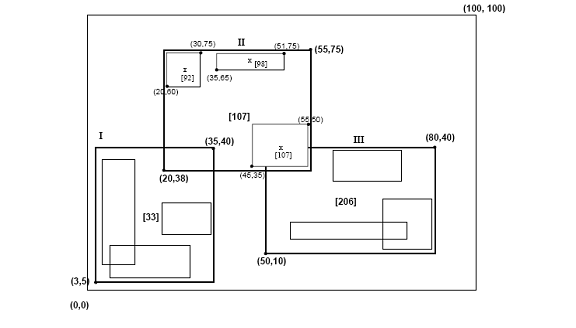
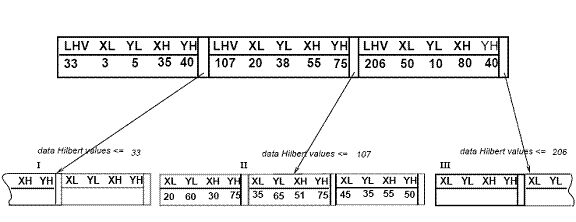
El árbol R de Hilbert tiene la siguiente estructura. Un nodo hoja contiene como máximo C _l entradas, cada una de la forma (R, obj_id) donde C _l es la capacidad de la hoja, R es el MBR del objeto real (x _low , x _high , y _low , y _high ) y obj-id es un puntero al registro de descripción del objeto. La principal diferencia entre el árbol R de Hilbert y el árbol R* ^[5] es que los nodos que no son hojas también contienen información sobre los LHV (valores de Hilbert más grandes). Por lo tanto, un nodo no hoja en el árbol R de Hilbert contiene como máximo C _n entradas de la forma (R, ptr, LHV) donde C _n es la capacidad de un nodo no hoja, R es el MBR que encierra todos los hijos de ese nodo, ptr es un puntero al nodo hijo y LHV es el valor de Hilbert más grande entre los rectángulos de datos encerrados por R. Observe que, dado que el nodo no hoja elige uno de los valores de Hilbert de los hijos para que sea el valor de su propio LHV, no hay un costo adicional para calcular los valores de Hilbert del MBR de los nodos no hoja. La Figura 3 ilustra algunos rectángulos organizados en un árbol R de Hilbert. Los valores de Hilbert de los centros son los números cerca de los símbolos "x" (mostrados solo para el nodo padre "II"). Los LHV están entre [corchetes]. La Figura 4 muestra cómo se almacena en el disco el árbol de la Figura 3; el contenido del nodo padre "II" se muestra con más detalle. Cada rectángulo de datos en el nodo "I" tiene un valor de Hilbert v ≤33; de manera similar, cada rectángulo en el nodo "II" tiene un valor de Hilbert mayor que 33 y ≤ 107, etc.

Figura 3: Rectángulos de datos organizados en un árbol R de Hilbert (los valores de Hilbert y los valores de Hilbert más grandes (LHV) están entre corchetes)

Un árbol R simple divide un nodo en caso de desbordamiento, lo que crea dos nodos a partir del original. Esta política se denomina política de división de 1 a 2. También es posible aplazar la división y esperar hasta que dos nodos se dividan en tres. Tenga en cuenta que esto es similar a la política de división del árbol B*. Este método se conoce como política de división de 2 a 3.

En general, esto se puede extender a una política de división de s a (s+1), donde s es el orden de la política de división. Para implementar la política de división de orden s, el nodo que se desborda intenta enviar algunas de sus entradas a uno de sus s - 1 hermanos; si todos están llenos, entonces se debe realizar la división de s a (s+1). Los s -1 hermanos se denominan hermanos cooperadores.

A continuación, se describen en detalle los algoritmos de búsqueda, inserción y manejo de desbordamientos.

El algoritmo de búsqueda es similar al utilizado en otras variantes del árbol R. Comenzando desde la raíz, desciende por el árbol y examina todos los nodos que intersecan el rectángulo de consulta. En el nivel de hoja, informa todas las entradas que intersecan la ventana de consulta como elementos de datos calificados.

Algoritmo de búsqueda (nodo raíz, rectángulo w):
S1. Búsqueda de nodos que no sean hojas:

Invocar Buscar para cada entrada cuyo MBR interseca la ventana de consulta w.

S2. Búsqueda de nodos de hoja:

Reportar todas las entradas que intersectan la ventana de consulta como candidatas.

Figura 4: La estructura de archivos para el árbol R de Hilbert

Para insertar un nuevo rectángulo r en el árbol R de Hilbert, se utiliza como clave el valor de Hilbert h del centro del nuevo rectángulo. En cada nivel se elige el nodo con el valor LHV mínimo mayor que h de todos sus hermanos. Cuando se llega a un nodo hoja, el rectángulo r se inserta en su orden correcto según h. Después de insertar un nuevo rectángulo en un nodo hoja N, se llama a AdjustTree para fijar el MBR y los valores de Hilbert más grandes en los nodos de nivel superior.

Algoritmo Insertar(nodo raíz, rectángulo r): /* Inserta un nuevo rectángulo r en el árbol R de Hilbert. h es el valor de Hilbert del rectángulo*/
I1. Busque el nodo de hoja apropiado:

Invoque ChooseLeaf(r, h) para seleccionar un nodo de hoja L en el que colocar r.

I2. Insertar r en un nodo hoja L:

Si L tiene una ranura vacía, inserte r en L en el

lugar apropiado según el orden de Hilbert y retorno.

Si L está lleno, invoca HandleOverflow(L,r), que

Volverá una nueva hoja si la división fuera inevitable,

I3. Propagar los cambios hacia arriba:

Formar un conjunto S que contenga a L, sus hermanos cooperadores

y la hoja nueva (si la hay)

Invocar AdjustTree(S).

I4. Haz que el árbol crezca más alto:

Si la propagación de la división del nodo provocó que la raíz se dividiera, cree

una nueva raíz cuyos hijos son los dos nodos resultantes.

Algoritmo ChooseLeaf(rect r, int h):
/* Devuelve el nodo de hoja en el que se colocará un nuevo rectángulo r. */
C1. Inicializar:

Establezca N como el nodo raíz.

C2. Control de hojas:

Si N es una hoja, devuelve N.

C3. Elegir subárbol:

Si N es un nodo que no es hoja, elija la entrada (R, ptr, LHV)

con un valor mínimo de LHV mayor que h.

C4. Descender hasta llegar a una hoja:

Establezca N en el nodo señalado por ptr y repita desde C2.

Algoritmo AdjustTree(set S):
/* S es un conjunto de nodos que contiene el nodo que se está actualizando, sus hermanos cooperadores (si se ha producido un desbordamiento) y el
nodo NN recién creado (si se ha producido una división). La rutina asciende desde el nivel de hoja hacia la raíz, ajustando MBR y LHV de los nodos que cubren los nodos en S. Propaga las divisiones (si las hay) */
A1. Si se alcanza el nivel raíz, se detiene.
A2. Propagar la división del nodo hacia arriba:

Sea Np el nodo padre de N.

Si N se ha dividido, sea NN el nuevo nodo.

Insertar NN en Np en el orden correcto según su Hilbert

Valor si hay espacio. De lo contrario, invocar HandleOverflow(Np, NN).

Si Np se divide, sea PP el nuevo nodo.

A3. Ajuste los MBR y LHV en el nivel principal:

Sea P el conjunto de nodos padres de los nodos en S.

Ajuste los MBR y LHV correspondientes de los nodos en P adecuadamente.

A4. Pasar al siguiente nivel:

Sea S el conjunto de nodos padre P, con

NN = PP, si Np se dividió.

repetir desde A1.

En el árbol R de Hilbert, no es necesario volver a insertar nodos huérfanos cada vez que un nodo padre presenta un desbordamiento. En cambio, las claves se pueden tomar prestadas de los hermanos o el nodo que presenta un desbordamiento se fusiona con sus hermanos. Esto es posible porque los nodos tienen un orden claro (según el valor de Hilbert más grande, LHV); por el contrario, en los árboles R no existe tal concepto en lo que respecta a los nodos hermanos. Observe que las operaciones de eliminación requieren s hermanos cooperadores, mientras que las operaciones de inserción requieren s - 1 hermanos.

Algoritmo Delete(r):
D1. Encuentra la hoja anfitriona:

Realice una búsqueda de coincidencia exacta para encontrar el nodo hoja L

que contiene r.

D2. Eliminar r :

Eliminar r del nodo L.

D3. Si L se desborda

tomar prestadas algunas entradas de los hermanos que cooperan.

Si todos los hermanos están dispuestos a desbordarse.

fusionar s + 1 a s nodos,

ajustar los nodos resultantes.

D4. Ajuste MBR y LHV en los niveles principales.

Formar un conjunto S que contenga a L y sus cooperadores.

hermanos (si se ha producido un desbordamiento).

invocar AdjustTree(S).

El algoritmo de manejo de desbordamiento en el árbol R de Hilbert trata los nodos desbordados moviendo algunas de las entradas a uno de los s - 1 hermanos cooperadores o dividiendo los nodos s en s +1 nodos.

Algoritmo HandleOverflow(nodo N, rect r):
/* devuelve el nuevo nodo si se produjo una división. */
H1. Sea ε un conjunto que contiene todas las entradas de N

y sus hermanos cooperadores s-1.

H2. Sumar r a ε.
H3. Si al menos uno de los s - 1 hermanos cooperadores no está completo,

distribuir ε uniformemente entre los nodos s según los valores de Hilbert.

H4. Si todos los hermanos cooperadores están completos,

crear un nuevo nodo NN y

distribuir ε uniformemente entre los nodos s + 1 de acuerdo

a los valores de Hilbert

devolver NN.

Wikimedia Commons alberga una categoría multimedia sobre Árbol R de Hilbert .

• I. Kamel y C. Faloutsos. Árboles R paralelos. En Proc. de la conferencia ACM SIGMOD, páginas 195-204, San Diego, CA, junio de 1992. También disponible como Informe técnico UMIACS TR 92-1, CS-TR-2820.
• I. Kamel y C. Faloutsos. Hilbert R-tree: An improved R-tree using fractals. En Proc. of VLDB Conf., páginas 500–509, Santiago, Chile, septiembre de 1994. También disponible como Tech_ Report UMIACS TR 93-12.1 CS-TR-3032.1.
• N. Koudas, C. Faloutsos e I. Kamel. Declustering Spatial Databases on a Multi-Computer Architecture, Conferencia internacional sobre la extensión de la tecnología de bases de datos (EDBT), páginas 592–614, 1996.
• N. Roussopoulos y D. Leifker. Búsqueda espacial directa en bases de datos pictóricas utilizando árboles R empaquetados. En Proc. of ACM SIGMOD, páginas 17–31, Austin, TX, mayo de 1985.
• M. Schroeder. Fractales, caos, leyes de potencia: minutos de un paraíso infinito. WH Freeman and Company, NY, 1991.
• T. Sellis, N. Roussopoulos y C. Faloutsos. El árbol R+: un índice dinámico para objetos multidimensionales. En Proc. 13th International Conference on VLDB, páginas 507–518, Inglaterra, septiembre de 1987.