Árbol de fusión

Este artículo puede resultar demasiado técnico para la mayoría de los lectores . Por favor, ayúdenos a mejorarlo para que sea comprensible para los no expertos , sin eliminar los detalles técnicos. ( Diciembre de 2017 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En informática , un árbol de fusión es un tipo de estructura de datos de árbol que implementa una matriz asociativa de números enteros de w bits en un universo finito, donde cada uno de los números enteros de entrada tiene un tamaño menor que 2 ^w y no es negativo. Cuando opera en una colección de n pares clave-valor , utiliza un espacio O ( n ) y realiza búsquedas en tiempo O (log _w n ) , lo que es asintóticamente más rápido que un árbol binario de búsqueda autoequilibrado tradicional , y también mejor que el árbol de van Emde Boas para valores grandes de  w . Alcanza esta velocidad mediante el uso de ciertas operaciones de tiempo constante que se pueden realizar en una palabra de máquina . Los árboles de fusión fueron inventados en 1990 por Michael Fredman y Dan Willard . ^[1]

Se han logrado varios avances desde el artículo original de Fredman y Willard de 1990. En 1999 ^[2] se mostró cómo implementar árboles de fusión bajo un modelo de computación en el que todas las operaciones subyacentes del algoritmo pertenecen a AC ⁰ , un modelo de complejidad de circuito que permite la adición y operaciones booleanas bit a bit pero no permite las operaciones de multiplicación utilizadas en el algoritmo de árbol de fusión original. En 1996 ^[3] se propuso una versión dinámica de árboles de fusión que utiliza tablas hash que coincidían con el tiempo de ejecución O (log _w n ) de la estructura original en expectativa. En 2007 ^[4] se propuso otra versión dinámica que utiliza árboles exponenciales que produce tiempos de ejecución en el peor de los casos de O (log _w n + log log n ) por operación. Finalmente, se demostró que los árboles de fusión dinámicos pueden realizar cada operación en tiempo O (log _w n ) de manera determinista. ^[5]

Esta estructura de datos implementa operaciones de agregar clave, quitar clave, buscar clave y buscar predecesor (próximo valor más pequeño) y sucesor (próximo valor más grande) para una clave dada. El resultado parcial del localizador de bits más significativo en tiempo constante también ha ayudado a la investigación. Los árboles de fusión utilizan paralelismo a nivel de palabra para ser eficientes, realizando cálculos en varios números enteros pequeños, almacenados en una sola palabra de máquina, simultáneamente para reducir la cantidad de operaciones totales.

Un árbol de fusión es esencialmente un árbol B con un factor de ramificación de w ^1/5 (cualquier exponente pequeño también es posible ya que no tendrá un gran impacto en la altura del árbol), lo que le da una altura de O (log _w n ) . Para lograr los tiempos de ejecución deseados para actualizaciones y consultas, el árbol de fusión debe poder buscar un nodo que contenga hasta w ^1/5 claves en tiempo constante. Esto se hace comprimiendo ("bosquejando") las claves para que todas puedan caber en una palabra de máquina, lo que a su vez permite que las comparaciones se realicen en paralelo. Por lo tanto, una serie de cálculos que involucran bosquejo, comparación paralela y localizador de índice de bit más significativo, ayudan a alcanzar la solución requerida.

El esbozo es el método por el cual cada clave de w bits en un nodo que contiene k claves se comprime en solo k − 1 bits. Cada clave x puede considerarse como un camino en el árbol binario completo de altura w que comienza en la raíz y termina en la hoja correspondiente a x . Este camino se puede procesar buscando recursivamente el hijo izquierdo de i si el bit i es 0, y el hijo derecho si es 1, generalmente, hasta que se hayan escaneado todos los bits. Para distinguir dos caminos, basta con mirar su punto de ramificación (el primer bit donde difieren dos claves cualesquiera). Como hay un máximo de k claves, no habrá más de k-1 puntos de ramificación, lo que significa que no se requieren más de k-1 bits para identificar una clave. Y, por lo tanto, ningún esbozo tendrá más de k-1 bits.

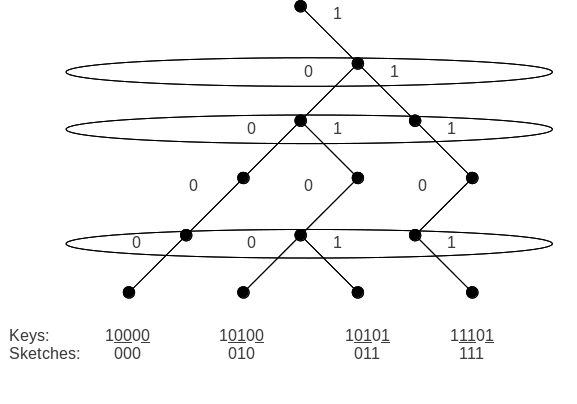
Una propiedad importante de la función sketch es que conserva el orden de las claves. Es decir, sketch( x ) < sketch( y ) para dos claves cualesquiera x < y . Por lo tanto, para todo el rango de claves, sketch(x ₀ )<sketch(x ₁ )<...<sketch(x _k-1 ) porque si se sigue la ruta de tipo árbol binario, los nodos se ordenarán de tal manera que x ₀ <x ₁ <...<x _k-1 .

Si las ubicaciones de los bits del boceto son b ₁ < b ₂ < ⋅⋅⋅ < b _r , entonces el boceto de la clave x _{w -1} ⋅⋅⋅ x ₁ x ₀ es el entero de r -bit .${\displaystyle x_{b_{r}}x_{b_{r-1}}\cdots x_{b_{1}}}$

Con solo operaciones de palabras estándar, como las del lenguaje de programación C , es difícil calcular directamente el boceto perfecto de una clave en tiempo constante. En cambio, los bits del boceto se pueden empaquetar en un rango de tamaño como máximo r ⁴ , utilizando AND a nivel de bits y multiplicación, llamado boceto aproximado, que tiene todos los bits importantes pero también algunos bits inútiles adicionales distribuidos en un patrón predecible. La operación AND a nivel de bits sirve como una máscara para eliminar todos estos bits que no son boceto de la clave, mientras que la multiplicación desplaza los bits del boceto a un rango pequeño. Al igual que el boceto "perfecto", el boceto aproximado también conserva el orden de las claves y significa que boceto(x ₀ )<boceto(x ₁ )<...<boceto(x _k-1 ).

Se necesita un preprocesamiento para determinar la constante de multiplicación correcta. Cada bit del boceto en la posición b _i se desplazará a b _i + m _i mediante una multiplicación por m = 2 ^{m _i} . Para que el boceto aproximado funcione, deben cumplirse las tres propiedades siguientes:${\displaystyle \textstyle \sum _ {i=1}^{r}}$

1. b _i + m _j son distintos para todos los pares ( i , j ). Esto garantizará que los bits del boceto no se corrompan con la multiplicación.
2. b _i + m _i es una función estrictamente creciente de i . Es decir, el orden de los bits del boceto se conserva incluso en x'.m.
3. ( b _r + m _r ) - ( b ₁ + m ₁ ) ≤ r ⁴ . Es decir, los bits del boceto se empaquetan en un rango de tamaño como máximo r ⁴ , donde r ≤ O(w ^1/5 ).

Un argumento inductivo muestra cómo se puede construir m _i . Sea m ₁ = w − b ₁ . Supóngase que 1 < t ≤ r y que ya se han elegido m ₁ , m ₂ ... m _t-1 . Entonces, escoja el entero más pequeño m _t tal que se satisfagan ambas propiedades (1) y (2). La propiedad (1) requiere que m _t ≠ b _i − b _j + m _l para todos los 1 ≤ i , j ≤ r y 1 ≤ l ≤ t -1. Por lo tanto, hay menos de tr ² ≤ r ³ valores que m _t debe evitar. Dado que se elige que m _t sea mínimo, ( b _t + m _t ) ≤ ( b _{t -1} + m _{t -1} ) + r ³ . Esto implica la propiedad (3).

El croquis aproximado se calcula así:

1. Enmascare todos los bits excepto los del boceto con un AND bit a bit entre x y .${\displaystyle \suma _{i=0}^{r-1}2^{b_{i}}}$
2. Multiplica la clave por la constante predeterminada m calculada anteriormente. Esta operación requiere dos palabras de máquina, pero puede realizarse en tiempo constante.
3. Oculte todos los bits excepto los del boceto desplazados. Estos ahora están contenidos en un bloque contiguo de, como máximo, r ⁴ < w ^4/5 bits.

El objetivo de la compresión que se logra mediante el esbozo es permitir que todas las claves se almacenen en una palabra de w bits. Sea el esbozo de nodo de un nodo la cadena de bits

1 sketch( x ₁ )1 sketch( x ₂ )...1 sketch( x _k )

Aquí, todas las palabras del boceto se agrupan en una cadena anteponiendo un bit de conjunto a cada una de ellas. Podemos suponer que la función de boceto utiliza exactamente b ≤ r ⁴ bits. Entonces, cada bloque utiliza 1 + b ≤ w ^4/5 bits y, dado que k ≤ w ^1/5 , la cantidad total de bits en el boceto del nodo es como máximo w .

Un breve comentario sobre notación: para una cadena de bits s y un entero no negativo m , sea s ^m la concatenación de s consigo mismo m veces. Si t también es una cadena de bits, st denota la concatenación de t con s .

El bosquejo de nodos permite buscar las claves para cualquier entero de b bits y . Sea z = (0 y ) ^k , que se puede calcular en tiempo constante (multiplicar y por la constante (0 ^b 1) ^k ), para que sea tan largo como el bosquejo de nodos de modo que cada palabra en el bosquejo de nodos se pueda comparar con el entero de consulta y en una operación, demostrando paralelismo a nivel de palabra. Si y tuviera 5 bits de longitud, se multiplicaría por 000001....000001 para obtener sketch(y) ^k . La diferencia entre sketch(x _i ) y 0y da como resultado que el bit inicial de cada bloque sea 1, si y solo si sketch(y) sketch(x _i ). De este modo, podemos calcular el índice i más pequeño tal que ( x _i ) ≥ y de la siguiente manera:${\estilo de visualización \leq}$sketch

1. Restar z del boceto del nodo.
2. Tome la operación AND bit a bit de la diferencia y la constante (10 ^b ) ^k . Esto borra todos los bits de cada bloque excepto el bit principal.
3. Encuentre la parte más significativa del resultado, para identificar el índice exacto de transición de los elementos con un boceto menor que el boceto de consulta a aquellos mayores que el boceto de consulta.
4. Calcule i, el rango del boceto, utilizando el hecho de que el bit principal del bloque i -ésimo tiene índice i ( b + 1).

Para una consulta arbitraria q , la comparación paralela calcula el índice i tal que

sketch( x _{i -1} ) ≤ sketch( q ) ≤ sketch( x _i )

Desafortunadamente, esto no da el predecesor o sucesor exacto de q , porque la ubicación del boceto de q entre los bocetos de todos los valores puede no ser la misma que la ubicación de q en todos los valores reales. Lo que es cierto es que, entre todas las claves, ya sea x _{i -1} o x _i tiene el prefijo común más largo con q . Esto se debe a que cualquier clave y con un prefijo común más largo con q también tendría más bits de boceto en común con q , y por lo tanto sketch( y ) estaría más cerca de sketch( q ) que cualquier sketch( x _j ).

La longitud del prefijo común más largo entre dos enteros de w bits a y b se puede calcular en tiempo constante hallando el bit más significativo del XOR bit a bit entre a y b . Esto se puede utilizar para enmascarar todos los prefijos comunes excepto el más largo.

Nótese que p identifica exactamente dónde se ramifica q a partir del conjunto de claves. Si el siguiente bit de q es 0, entonces el sucesor de q está contenido en el subárbol p 1, y si el siguiente bit de q es 1, entonces el predecesor de q está contenido en el subárbol p 0. Esto sugiere el siguiente algoritmo para determinar la ubicación exacta de q :

1. Utilice la comparación paralela para encontrar el índice i tal que sketch( x _{i -1} ) ≤ sketch( q ) ≤ sketch( x _i ).
2. Calcule el prefijo común más largo p de q y x _{i -1} o x _i (tomando el más largo de los dos).
3. Sea l -1 la longitud del prefijo común más largo p .
   1. Si el bit l -ésimo de q es 0, sea e = p 10 ^{w - l} . Utilice la comparación paralela para buscar el sucesor de sketch( e ). Este es el predecesor real de q .
   2. Si el bit l -ésimo de q es 1, sea e = p 01 ^{w - l} . Utilice la comparación paralela para buscar el predecesor de sketch( e ). Este es el sucesor real de q .
4. Una vez que se encuentra el predecesor o sucesor de q , se determina la posición exacta de q entre el conjunto de claves.

Willard aplicó una aplicación de los árboles de fusión a las tablas hash al describir una estructura de datos para el hash en la que una tabla hash de nivel externo con encadenamiento hash se combina con un árbol de fusión que representa cada cadena hash. En el encadenamiento hash, en una tabla hash con un factor de carga constante, el tamaño promedio de una cadena es constante, pero además, con alta probabilidad, todas las cadenas tienen un tamaño O (log n / log log n ) , donde n es el número de elementos hash. Este tamaño de cadena es lo suficientemente pequeño como para que un árbol de fusión pueda manejar búsquedas y actualizaciones dentro de él en un tiempo constante por operación. Por lo tanto, el tiempo para todas las operaciones en la estructura de datos es constante con alta probabilidad. Más precisamente, con esta estructura de datos, para cada probabilidad inversa- cuasipolinómica p ( n ) = exp((log n ) ^{O (1)} ) , existe una constante C tal que la probabilidad de que exista una operación que exceda el tiempo C es como máximo p ( n ) . ^[6]

El modelo computacional para el algoritmo Fusion Tree es una Word RAM con un conjunto de instrucciones específico, que incluye instrucciones aritméticas: suma, resta y multiplicación (todas realizadas módulo 2 ^w ) y operaciones booleanas: AND, NOT bit a bit, etc. También se incluye una instrucción de multiplicación de doble precisión. Se ha demostrado ^[7] que la eliminación de la última instrucción hace imposible ordenar más rápido que O ( n log n ) , a menos que se permita usar espacio de memoria de casi 2 ^w palabras (en contraste con el espacio lineal utilizado por Fusion Trees), o incluir otras instrucciones en su lugar ^[2] .

• MIT CS 6.897: Estructuras de datos avanzadas: lección 4, árboles de fusión, profesor Erik Demaine (primavera de 2003)
• MIT CS 6.897: Estructuras de datos avanzadas: Clase 5, Más árboles de fusión; estructuras de datos autoorganizadas, movimiento al frente, optimalidad estática, Prof. Erik Demaine (primavera de 2003)
• MIT CS 6.851: Estructuras de datos avanzadas: Conferencia 13, notas de Fusion Tree, Prof. Erik Demaine (primavera de 2007)
• MIT CS 6.851: Estructuras de datos avanzadas: Conferencia 12, notas de Fusion Tree, Prof. Erik Demaine (primavera de 2012)